verilog中的定点数、浮点数、定点小数、定点整数的表示及运算_verilog浮点数

1、定点数：

                    顾名思义定点数就是小数位固定不变的数叫做定点数，也就是小数点是定在某个位置不变的数。

 2、定点数的分类：

                  （1）定点整数：定点整数的小数点后面没有其他的数值,即小数点定在了数的最后面

                          定点整数又分为以下两类：

                          @@：无符号的定点整数：Unsigned fixed point integer，无符号定点整数没有符号位，所以它的全部数位都用来表示数字，且它的小数点隐含在最低位后，在它的二进制形式中不存在小数点（数在计算机中都是以二进制的形式进行存储的）。

                          对于某种数的表示方式，我们关心两点：

                          1.表示范围：这种方法表示数的大小（正负方向）,无符号定点整数范围：0~2n-1

                          2.分辨率：精度,1（即最小非零正数）

                         二进制数：XnXn-1...X1X0表示无符号定点整数，则有n+1位正整数，它所代表的十进制数大小为：

                        

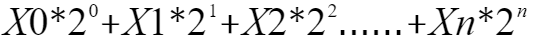
                       例如8位无符号二进制数的表示范围为：00000000-11111111：0-255

                       @@：带符号定点整数

                       定义：带符号定点整数是纯整数，小数点在最低位之后，最高位为符号位，它与无符号定点整数的区别就是它的                                       最高位只用来指示符号，不代表实际数值，并且它在计算机中以而二进制的补码形式存储。

                                   

                          XnXn-1...X1X0表示无符号定点整数(假设是原码形式)，则有n+1位正整数，它所代表的十进制数大小为：

                        

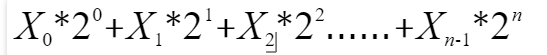
                         最高位为0代表正数，最高位为1代表负数。

                       例如8位有符号二进制数的表示范围为：00000000-11111111：-128 到127

（2）有符号定点小数：

                    

            定点小数即纯小数（但好多博客都说小数的位数和正数的位数可以事先约定，那这样的话就不是纯小数了，这一点还有疑惑），小数点的位置固定在最高有效数位之前、符号位之后，如图1所示。定点小数的小数点位置是隐含约定的，小数点并不需要真正地占据一个bit。

                  
                                                                      图1 定点小数格式
    当 Xs = 0 时，该小数为正值，其原码和补码表示的形式相同。

    其中，

    ⑴ 绝对值最大的正小数为：

                                                                  

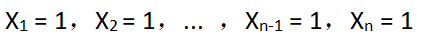
     其实际值等于（通过移项及合并同类项，可知该等式成立）： 

                             

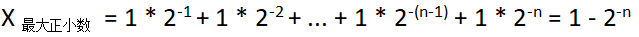
    ⑵ 绝对值最小的正小数为： 

                                           

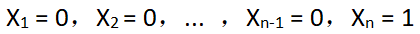
    其实际值等于： 

                                           

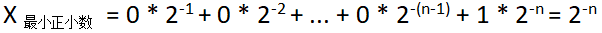
    以8bit数为例，最大正小数为 0.111 1111 = 1 - 2⁻⁷；最小正小数为 0.000 0001 = 2⁻⁷

    当 Xs = 1 时，该小数为负值，有原码和补码两种表示形式（以下形式包含Xs位）。 

    ⑴ 绝对值最大的负小数

        ① 原码表示

                    

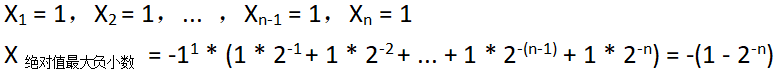
         ② 补码表示

                     

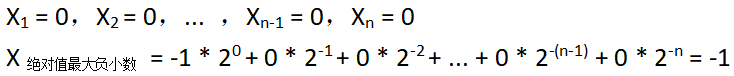
    ⑵ 绝对值最小的负小数

        ① 原码表示

                    

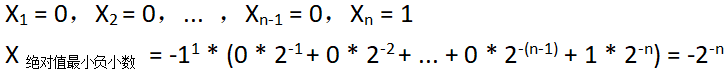
         ② 补码表示

                         

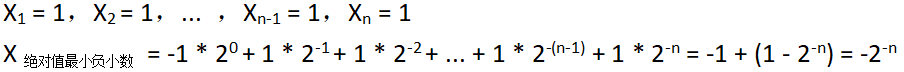
    可见，定点负小数的原码表示范围为: -(1 - 2⁻ⁿ) ~ -2⁻ⁿ；其补码表示范围为：-1 ~ -2⁻ⁿ。且n值越大，精度越高。

3.verilog中的定点小数

         程序指定小数点的位置即为定标，有两种方法：Q表示方法和S表示方法。
(1) Q表示法：Qn表示低n位为小数，其余位为符号位和整数位。
(2) S表示法：Sn中低（15-n）为小数，其余位符号位和整数位。
在使用XILINX VIVADO 中的IP核，都是以Q表示法表示。

                    定点小数的表示范围：

              

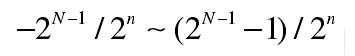
其中N为定点数的位数（排除符号位）,n为定标的位数，其中n越大则数据越精确，但表示的范围也会越小。

           假设有一个16位的变量，设定小数占8位，那么它的精度为8位，那么它的精度是多少呢？ 其实就是1/2^8=0.00390625.

          （0.5，0.25，0.125，0.0625，0.03125，0.015625，0.0078125，0.00390625）

         例如：reg [15:0] a=16'b0111_1011_1111_0000             它表示的定点小数为：31728/(2^8) = 123.9375也就是：

                 01111011.11110000的十进制数值

 

        假设一个数2.3，它的二进制形式为10.0100110........后面有无穷多位；但约定好小数的位数为5位之后，则这个数就成为了2.28125，小数的位数越多。精度越高，越接近其真值；

          

     那么我们假设x，x1，x2为实际小数，y1，y2，y3为定点小数，定位精度是n位，有如下关系

y1=y2+y3 <<=>>x1=x2+x3

y1=y2-y3 <<=>>x1=x2-x3

y1=y2/2^n*y3 <<=>>x1=x2*x3

y1=y2*2^n/y3 <<=>>x1=x2/x3

加减比较好理解，乘除为什么需要移位呢？以乘法为例子

y1=x1*2^n

y2*y3=x2*x3*x^2n                  ==>>y1*2^n=y2*y3 证毕
 

4.浮点数

      浮点数是一种 公式化 的表达方式，用来近似表示实数（浮点数也是实数），并且可以在表达范围和表示精度之间进行权衡（因此被称为浮点数）。

浮点数通常被表示为：

N=M×R^E

比如： 12.345=1.2345×10^1

其中，M(Mantissa)被称为浮点数的 尾数 ，R(Radix)被称为阶码的 基数 ，E(Exponent)被称为阶的 阶码 。计算机中一般规定R为2、8或16，是一个确定的常数，不需要在浮点数中明确表示出来。

因此，在已知标准下，要表示浮点数，

一是要给出尾数M的值，通常用定点小数形式表示（这里表示：纯小数），它决定了浮点数的表示精度，即可以给出的有效数字的位数。

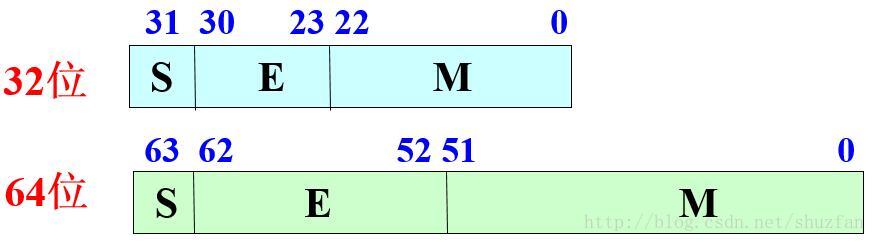
二是要给出阶码，通常用定点整数形式表示，它指出的是小数点在数据中的位置，决定了浮点数的表示范围。因此，在计算机中,浮点数通常被表示成如下格式:（假定为32位浮点数，基为2，其中最高位为符号位）

32位浮点数：

                      

            

64位浮点数：

              

       

浮点数的规格化表示 

按照上面的指数表示方法，一个浮点数会有不同的表示：

0.3×10^0；0.03×10^1；0.003×10^2；0.0003×10^3；

为了提高数据的表示精度同时保证数据表示的唯一性，需要对浮点数做规格化处理。

在计算机内，对非0值的浮点数，要求尾数的绝对值必须大于基数的倒数，即|M|≥1/R。

即要求尾数域的最高有效位应为1,称满足这种表示要求的浮点数为规格化表示：把不满足这一表示要求的尾数，变成满足这一要求的尾数的操作过程，叫作浮点数的规格化处理，通过尾数移位和修改阶码实现。

比如，二进制原码的规格化数的表现形式：(0正1负)

正数 0.1xxxxxx

负数 1.1xxxxxx

为了提高数据的表示精度，当尾数的值不为0时，尾数域的最高有效位应为1，这称为浮点数的规格化表示。否则以修改阶码同时左右移动小数点位置的办法，使其变成规格化数的形式。

 

至此，我们引入IEEE754 标准，该标准约束了浮点数的大部分使用设置：(尾数用原码；阶码用“移码”；基为2)

在IEEE754标准中，一个规格化的32位浮点数x的真值表示为
x = （-1） ^s X（1.M）X 2^（E-127）
e = E - 127
其中尾数域所表示的值是1.M。由于规格化的浮点数的尾数域最左位（最高有效位）总是1，故这一位经常不予存储，而认为隐藏在小数点的左边。于是用23位字段可以存储24位有效数。(没有理解为啥这样)

64位的浮点数中符号位1位，阶码域11位，尾数域52位，植树偏移值是1023.因此规格化的64位浮点数x的真值为
x = （-1）s X（1.M）X 2^（E-1023）
e = E - 1023

总结如下:

(1) 尾数用原码,且隐藏尾数最高位。

原码非0值浮点数的尾数数值最高位必定为 1，因此可以忽略掉该位,这样用同样多的位数就能多存一位二进制数，有利于提高数据表示精度，称这种处理方案使用了隐藏位技术。当然，在取回这样的浮点数到运算器执行运算时，必须先恢复该隐藏位。

(2) 阶码使用“移码”，基固定为2

如下图的32bit浮点数和64bit浮点数，从最高位依次是符号位、阶码和尾数 

于是，

一个规格化的32位浮点数ｘ的真值为：

x=(−1)^s×(1.M)×2E^−127

一个规格化的64位浮点数ｘ的真值为：

x=(−1)^s×(1.M)×2E^−1023

下面举一个32位单精度浮点数-3.75表示的例子帮助理解：

(1) 首先转化为2进制表示

−3.75=−(2+1+1/2+1/4)=−1.111×2^1

(2) 整理符号位并进行规格化表示

−1.111×2^1=(−1)^(1)×(1+0.1110 0000 0000 0000 0000 000)×2^1

(3) 进行阶码的移码处理 
(−1)^(1)×(1+0.1110 0000 0000 0000 0000 000)×2^1
 
=(−1)^(1)×(1+0.1110 0000 0000 0000 0000 000)×2^(128−127)

于是，符号位S=1，尾数M为1110 0000 0000 0000 0000 000
阶码E为12810=1000 00002
,则最终的32位单精度浮点数为

1 1110 0000 0000 0000 0000 000 1000 0000

例题
1. 问题： 若浮点数x的754标准存储格式为（41360000）16，求其浮点数的十进制数值。
解：将16进制数展开后，可得二进制数格式为

指数e=阶码-127=10000010-01111111=00000011=（3）10
包括隐藏位1的尾数1.M=1.011 0110 0000 0000 0000 0000=1.011011
于是有
x=（-1）^S X 1.M X 2^e=+（1.011011） X 2^3 = +1011.011=（11.375）10

2. 问题： 将数（20.59375）10转换成754标准的32位浮点数的二进制存储格式。
解：首先分别将整数和小数部分转换成二进制数：
20.59375 = 10100.10011
然后移动小数点，使其在第1、2位之间
10100.10011 = 1.010010011 X 2^4 e = 4
于是得到
S = 0， E = 4 + 127 = 131， M = 010010011
最后得到32位浮点数的二进制存储格式为
0100 0001 1010 0100 1100 0000 0000 0000 = （41A4C000）16
 

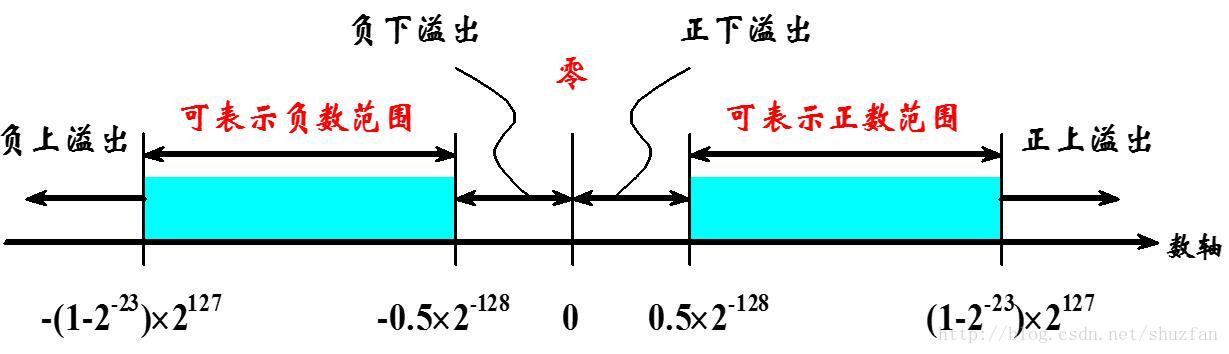
浮点数表示范围：

通过上面的规格化表示，我们可以很容易确定浮点数的表示范围：

 

 

既然有表示范围，那肯定也有不能表示的数值： 
首先来说明溢出值，如下图： 

 

(1)无穷值：

如果指数E=11111111(2)=255(10)
且尾数M=0
，则根据符号位S分别表示+∞
和−∞
。因此，一个有效的32位浮点数其指数最大只能为254。

此外，无穷具有传递性，比如

(+∞) + (+7) = (+∞)

(+∞) × (−2) = (−∞)

(+∞) × 0 = NaN

(2)零值：

如果指数E=0
且尾数M=0
时，表示机器0.需要注意的是，这里的0也是有符号的，在数值比较的时候 +0=−0
； 但在一些特殊操作下，二者并不显相等，比如log(x), 1/+0≠1/−0。

此外，处于负下溢出和负上溢出之间的数值会被直接归为0。

(3)NAN：

如果E=0,且尾数M≠0，则表示这个值不是一个真正的值（Not A Number）。NAN又分成两类：QNAN（Quiet NAN）和SNAN（Singaling NAN）。QNAN与SNAN的不同之处在于，QNAN的尾数部分最高位定义为1，SNAN最高位定义为0；QNAN一般表示未定义的算术运算结果，如0/0, ∞×0, sqrt(−1)；SNAN一般被用于标记未初始化的值，以此来捕获异常。

 

浮点数的表示精度

一般提到浮点数的精度（有效位数）的时候，总是会出现 float的有效位为6~7位, double的有效位为15~16位 。

下面以float为例，解释一下有效位数是怎样来的。

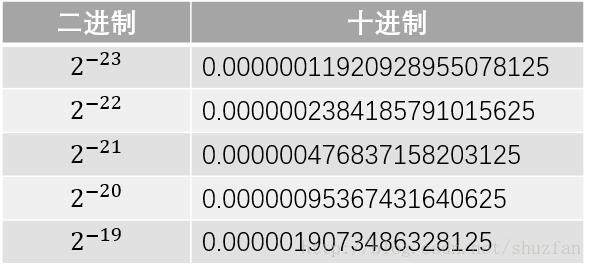
有效位数只和规格化浮点数的尾数部分有关，而尾数部分的位数是23位，因此我们首先列出下表

由上面的表格可以看出：

2^−23 和 2^−22 之间是存在间隔的，即0.0000001和0.0000002之间的小数我们是没有办法描述的，因此23位尾数最多只能描述到小数点后第7位；此外，我们通过四舍五入可以很容易发现0.0000003=0.0000004=2^−23+2^−22
, 这表明第7位有效数字只是部分准确。而第6位及之前的都是可以准确描述的，因此我们说float的有

 

以上内容只是网上内容的总结与整合，所以也不是原创；

https://blog.csdn.net/qq_43164708/article/details/105178210

https://www.cnblogs.com/Mayfly-nymph/p/11090241.html

https://blog.csdn.net/qq_43164708/article/details/105178210