简单解析B树(B-tree)与B+树_b+树和b树查询时间复杂度

B-树就是B树

引言:二叉查找树时间复杂度为O(logN),效率很高,但是由于磁盘IO要求,我们需要一种矮胖的结构来减少加载磁盘页(每个磁盘页随影树的节点)的次数,提高磁盘IO效率,因此就有了B树和B+树.称为多路查找树.

 

B树:

一个m阶的B树具有如下几个特征：B树中所有结点的孩子结点最大值称为B树的阶，通常用m表示。一个结点有k个孩子时，必有k-1个关键字才能将子树中所有关键字划分为k个子集。

1.根结点至少有两个子女。
2.每个中间节点都包含k-1个元素和k个孩子，其中 ceil（m/2） ≤ k ≤ m
3.每一个叶子节点都包含k-1个元素，其中 ceil（m/2） ≤ k ≤ m
4.所有的叶子结点都位于同一层。
5.每个节点中的元素从小到大排列，节点当中k-1个元素正好是k个孩子包含的元素的值域划分
6.每个结点的结构为：（n，A0，K1，A1，K2，A2，…  ，Kn，An）
    其中，Ki(1≤i≤n)为关键字，且Ki<Ki+1(1≤i≤n-1)。
Ai(0≤i≤n)为指向子树根结点的指针。且Ai所指子树所有结点中的关键字均小于Ki+1。
n为结点中关键字的个数，满足ceil(m/2)-1≤n≤m-1。

 

查询
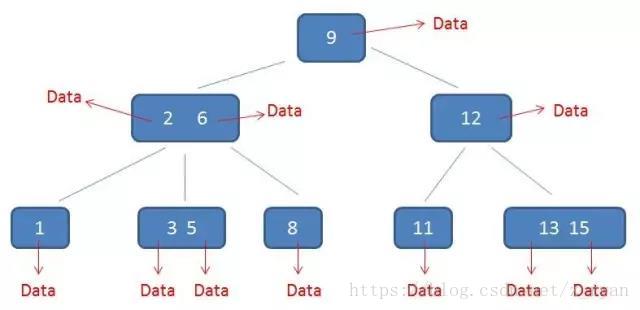
　　以上图为例：若查询的数值为５： 
　　第一次磁盘ＩＯ：在内存中定位（与17、35比较），比17小，左子树； 
　　第二次磁盘ＩＯ：在内存中定位（与８、12比较），比８小，左子树； 
　　第三次磁盘ＩＯ：在内存中定位（与3、5比较），找到5，终止。 
整个过程中，我们可以看出：比较的次数并不比二叉查找树少，尤其适当某一节点中的数据很多时，但是磁盘IO的次数却是大大减少。比较是在内存中进行的，相比于磁盘IO的速度，比较的耗时几乎可以忽略。所以当树的高度足够低的话，就可以极大的提高效率。相比之下，节点中的元素多点也没关系，仅仅是多了几次内存交互而已，只要不超过磁盘页的大小即可。

插入
　　对高度为ｋ的m阶B树，新结点一般是插在叶子层。通过检索可以确定关键码应插入的结点位置。然后分两种情况讨论： 
　　1、 若该结点中关键码个数小于m-1，则直接插入即可。 
　　2、 若该结点中关键码个数等于m-1，则将引起结点的分裂。以中间关键码为界将结点一分为二，产生一个新结点，并把中间关键码插入到父结点(ｋ-1层)中 
　　重复上述工作，最坏情况一直分裂到根结点，建立一个新的根结点，整个B树增加一层。

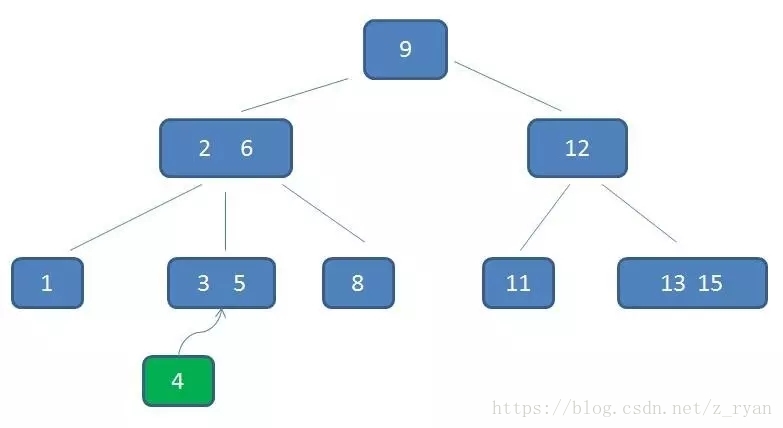
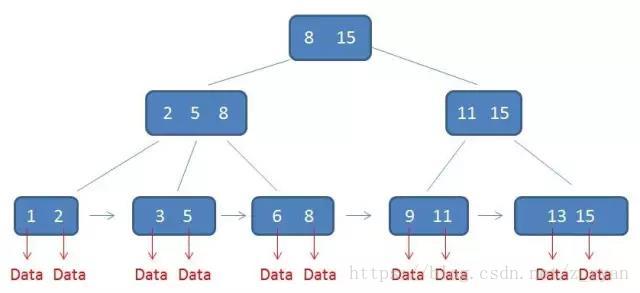
例如：在下面的B树中插入key：4

第一步：检索key插入的节点位置如上图所示，在3,5之间；

第二步：判断节点中的关键码个数： 
　　节点3，5已经是两元素节点，无法再增加。父亲节点 2， 6 也是两元素节点，也无法再增加。根节点9是单元素节点，可以升级为两元素节点。；

第三步：结点分裂： 
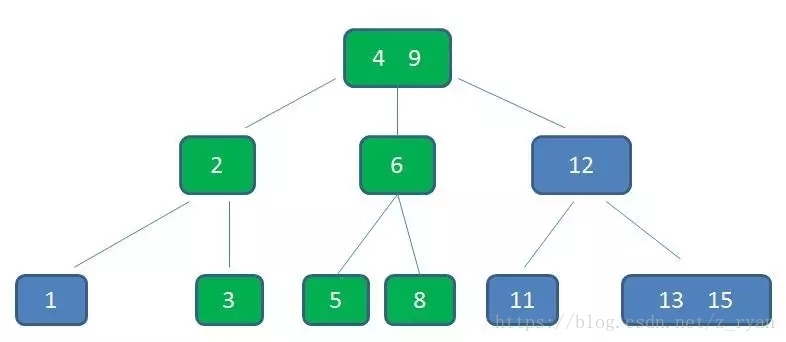
　　拆分节点3，5与节点2，6，让根节点9升级为两元素节点4，9。节点6独立为根节点的第二个孩子。

最终结果如下图：虽然插入比较麻烦，但是这也能确保Ｂ树是一个自平衡的树 

 

删除

　　Ｂ树中关键字的删除比插入更复杂，在这里，只介绍其中的一种方法： 
　　 
　　在B树上删除关键字k的过程分两步完成：

（1）找出该关键字所在的结点。然后根据 k所在结点是否为叶子结点有不同的处理方法。

（2）若该结点为非叶结点，且被删关键字为该结点中第i个关键字key[i]，则可从指针son[i]所指的子树中 找出最小关键字Y，代替key[i]的位置，然后在叶结点中删去Y。

 因此，把在非叶结点删除关键字k的问题就变成了删除叶子结点中的关键字的问题了。

叶结点上删除一个关键字的方法： 
　　首先将要删除的关键字 k直接从该叶子结点中删除。然后根据不同情况分别作相应的处理，共有三种可能情况：

（1）如果被删关键字所在结点的原关键字个数n>=ceil(m/2)，说明删去该关键字后该结点仍满足B树的定义。
这种情况最为简单，只需从该结点中直接删去关键字即可。

（2）如果被删关键字所在结点的关键字个数n等于ceil(m/2)-1，说明删去该关键字后该结点将不满足B树的定义，
需要调整。

调整过程为：
   如果其左右兄弟结点中有“多余”的关键字,即与该结点相邻的右（左）兄弟结点中的关键字数目大于
ceil(m/2)-1。则可将右（左）兄弟结点中最小（大）关键字上移至双亲结点。而将双亲结点中小（大）于该上
移关键字的关键字下移至被删关键字所在结点中。
   如果左右兄弟结点中没有“多余”的关键字，即与该结点相邻的右（左）兄弟结点中的关键字数目均等于
ceil(m/2)-1。这种情况比较复杂。需把要删除关键字的结点与其左（或右）兄弟结点以及双亲结点中分割二者
的关键字合并成一个结点,即在删除关键字后，该结点中剩余的关键字加指针，加上双亲结点中的关键字Ki一起，
合并到Ai（是双亲结点指向该删除关键字结点的左（右）兄弟结点的指针）所指的兄弟结点中去。如果因此使双亲
结点中关键字个数小于ceil(m/2)-1，则对此双亲结点做同样处理。以致于可能直到对根结点做这样的处理而使
整个树减少一层。

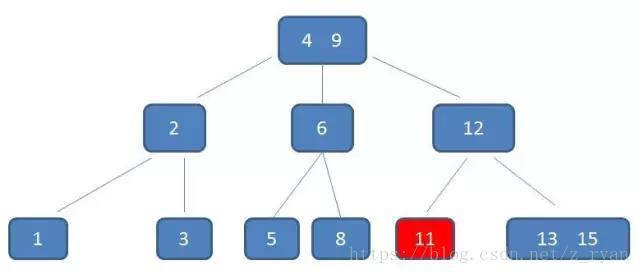
 下面举一个简单的例子：删除元素11. 

第一步：判断该元素是否在叶子结点上。 
　　　该元素在叶子节点上，可以直接删去，但是删除之后，中间节点12只有一个孩子，不符合B树的定义：每个中间节点都包含k个孩子，（其中 ceil（m/2） <= k <= m）所以需要调整；

第二步：判断其左右兄弟结点中有“多余”的关键字，即：原关键字个数n>=ceil(m/2) - 1； 
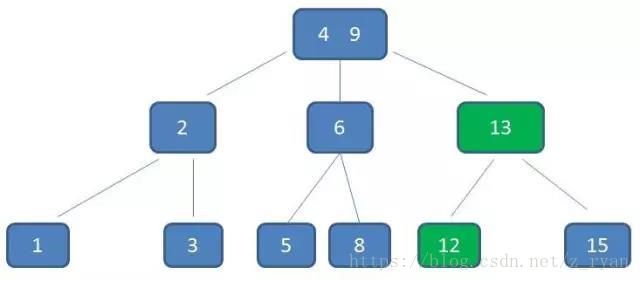
　　显然结点11的右兄弟节点中有多余的关键字。那么可将右兄弟结点中最小关键字上移至双亲结点。而将双亲结点中小于该上移关键字的关键字下移至被删关键字所在结点中即可

 

注意
　　①、B树主要用于文件系统以及部分数据库索引，例如： MongoDB。而大部分关系数据库则使用B+树做索引，例如：mysql数据库； 
　　②、从查找效率考虑一般要求B树的阶数m >= 3; 
　　③、B树上算法的执行时间主要由读、写磁盘的次数来决定，故一次I/O操作应读写尽可能多的信息。因此B-树的结点规模一般以一个磁盘页为单位。一个结点包含的关键字及其孩子个数取决于磁盘页的大小。
B+树:

Ｂ树的变种，有着比Ｂ树更高的查询效率。

前面已经提到,磁盘IO是不使用二叉查找树的主要原因,那么是不是有一种结构比B树更能减少磁盘IO损失呢?那就是B+树

一个很重要的原因是B+树只有叶子节点存储元素信息,因此他加载的磁盘页更少(个人理解是因为一个磁盘页可以存储多个元素)

特点:

一个m阶的B+树具有如下几个特征：

1.有k个子树的中间节点包含有k个元素（B树中是k-1个元素），每个元素不保存数据，只用来索引，所有数据
都保存在叶子节点。

2.所有的叶子结点中包含了全部元素的信息，及指向含这些元素记录的指针，且叶子结点本身依关键字的大小
自小而大顺序链接。

3.所有的中间节点元素都同时存在于子节点，在子节点元素中是最大（或最小）元素。

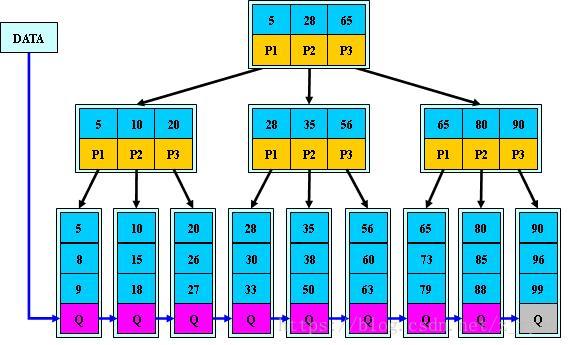
 下面是一棵3阶的B+树： 

B+树通常有两个指针，一个指向根结点，另一个指向关键字最小的叶子结点。因些，对于B+树进行查找两种运算：一种是从最小关键字起顺序查找，另一种是从根结点开始，进行随机查找。(没看懂)

查找
　　B+树的优势在于查找效率上，下面我们做一具体说明： 
　　首先，Ｂ＋树的查找和Ｂ树一样，类似于二叉查找树。起始于根节点，自顶向下遍历树，选择其分离值在要查找值的任意一边的子指针。在节点内部典型的使用是二分查找来确定这个位置。 
　　（1）、不同的是，Ｂ＋树中间节点没有卫星数据（索引元素所指向的数据记录），只有索引，而Ｂ树每个结点中的每个关键字都有卫星数据；这就意味着同样的大小的磁盘页可以容纳更多节点元素，在相同的数据量下，Ｂ＋树更加“矮胖”，ＩＯ操作更少 
　B树的卫星数据： 

B+树的卫星数据：

需要补充的是，在数据库的聚集索引（Clustered Index）中，叶子节点直接包含卫星数据。在非聚集索引（NonClustered Index）中，叶子节点带有指向卫星数据的指针。 (这一块个人理解应该是非聚集索引叶子节点为聚集索引的叶子节点的值,如果通过非聚集索引查找,则找到的是对应的聚集索引的值,再到聚集索引查找具体值)

（2）、其次，因为卫星数据的不同，导致查询过程也不同；Ｂ树的查找只需找到匹配元素即可，最好情况下查找到根节点，最坏情况下查找到叶子结点，所说性能很不稳定，而Ｂ＋树每次必须查找到叶子结点，性能稳定 

3）、在范围查询方面，B+树的优势更加明显 
　　B树的范围查找需要不断依赖中序遍历。首先二分查找到范围下限，在不断通过中序遍历，知道查找到范围的上限即可。整个过程比较耗时。 
　　而B+树的范围查找则简单了许多。首先通过二分查找，找到范围下限，然后同过叶子结点的链表顺序遍历，直至找到上限即可，整个过程简单许多，效率也比较高。 

插入
　　 B+树的插入与B树的插入过程类似。不同的是B+树在叶结点上进行，如果叶结点中的关键码个数超过m，就必须分裂成关键码数目大致相同的两个结点，并保证上层结点中有这两个结点的最大关键码。

删除
　　B+树中的关键码在叶结点层删除后，其在上层的复本可以保留，作为一个”分解关键码”存在，如果因为删除而造成结点中关键码数小于ceil(m/2)，其处理过程与B-树的处理一样。在此，我就不多做介绍了。(删除操作比较复杂,留作以后补充学习内容)

总结
B+树相比B树的优势： 
　　1.单一节点存储更多的元素，使得查询的IO次数更少； 
　　2.所有查询都要查找到叶子节点，查询性能稳定； 
　　3.所有叶子节点形成有序链表，便于范围查询。
 

原文：https://blog.csdn.net/z_ryan/article/details/79685072