【Python】圆周率 Pi (π) 的计算（蒙特卡罗法+公式法）_用python计算圆周率

引言

圆周率（Pi）是圆的周长与直径的比值，一般用希腊字母 π 表示，是数学中最重要和最奇妙的数字之一。本文教你如何使用 Python 编程实现圆周率的简单计算。

计算

蒙特卡罗法

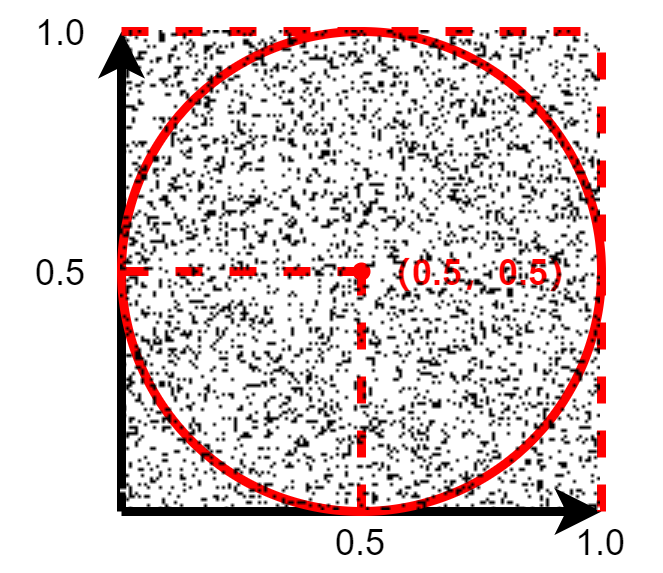
1×1 的正方形里面有一个内切圆。向该正方形区域内随机散点（散点总数记为 S），对于每一个点，其落在圆内的概率是：$\frac{\pi \cdot 0.5^2}{1\times 1}=0.25\pi$，散点结束后，统计其落在圆内的点数，并记为 N。

一般来说，随着实验次数的增多，频率会接近于概率。当实验次数趋向于无穷时，频率的极限就是概率。

因此，当 S 足够大时，我们可以简单认为：$0.25\pi =\frac{N}{S}$，即$\pi =\frac{4N}{S}$

提示：如何判断点在圆内？计算点到圆心的欧式距离，比半径小就在圆内，比半径大就在圆外。

# 蒙特卡罗法（统计试验法）
import random # 导入随机模块
S = 1e6 # 变量S为试验总次数（值设置得越大，PI的计算越准确，即频率越逼近于概率）
N = 0 # 变量N用于统计落在圆内的试验点的个数
for i in range(int(S)):
    x = random.random() # 获取0-1之间的随机数
    y = random.random() # 获取0-1之间的随机数
    d = (x-0.5)**2+(y-0.5)**2 # 计算试验点到圆心的欧式距离的平方
    if d<=0.5**2: # 通过比较试验点到圆心的欧式距离与圆半径的大小，判断该点是否在圆内
        N+=1
    else:
        pass
PI = 4*N/S
print(PI)
1
2
3
4
5
6
7
8
9
10
11
12
13
14

公式法

$$\pi =\sum _{n=0}^{\infty }[\frac{1}{16^n}(\frac{4}{8n+1}-\frac{2}{8n+4}-\frac{1}{8n+5}-\frac{1}{8n+6})]$$

# 公式法（计算公式参上）
PI = 0
N = 1000
for n in range(int(N)):
    PI += 1/pow(16,n) * (4/(8*n+1) - 2/(8*n+4) - 1/(8*n+5) - 1/(8*n+6))
print(PI)
1
2
3
4
5
6

参考

https://baike.baidu.com/item/圆周率/139930