扬州大学2022年858程序设计与数据结构试题参考答案_2022扬大858真题

作者：IT小白 | 2024-05-04 02:06:21

踩

2022扬大858真题

扬州大学 2022年硕士研究生招生考试初试试题（A卷）参考答案 科目代码：858 科目名称：程序设计与数据结构满分：150分

注意：答案为个人自制，非官方答案。

一、应用题

参考答案
例如，有一张学生基本信息表，包括学生的学号、姓名、性别、籍贯、专业等。每个学生的基本信息记录对应一个数据元素，学生记录按顺序号排列，形成了学生基本信息记录的线性序列。对于整个表来说，只有一个开始结点(它的前面无记录)和一个终端结点(它的后面无记录)，其他的结点则各有一个也只有一个直接前驱和直接后继。学生记录之间的这种关系就确定了学生表的逻辑结构，即线性结构。这些学生记录在计算机中的存储表示就是存储结构。如果用连续的存储单元(如用数组表示)）来存放这些记录，则称为顺序存储结构；如果存储单元不连续，而是随机存放各个记录，然后用指针进行链接,则称为链式存储结构。即相同的逻辑结构，可以对应不同的存储结构。
参考答案
H(H(T(H(T(H(T(L)))))))。
参考答案
(1) 或为空树,或为只有根结点的二叉树。
(2) 或为空树,或为任一结点至多只有左子树的二叉树。
(3) 或为空树,或为任一结点至多只有右子树的二叉树。
(4) 或为空树，或为任一结点至多只有右子树的二叉树。
参考答案
(1) 哈夫曼树如下图所示，其编码如下表所示。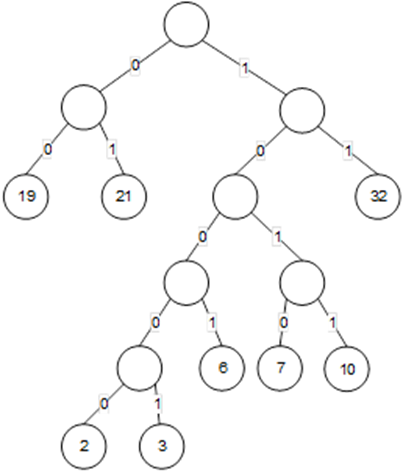

字母频率哈夫曼编码等长二进制编码
0.07 1010 000
0.19 00 001
0.02 10000 010
0.06 1001 011
0.32 11 100
0.03 10001 101
0.21 01 110
0.10 1011 111
(2) 二进制等长编码如上表所示。
(3) 对于上述两种方案，等长编码的构造显然比哈夫曼编码的构造简单。但是，哈夫曼编码是最优前缀编码，其加权路径长度为2.61，而等长二进制编码的加权路径长度为3。
参考答案
(1) 邻接矩阵如下
$\left\{ ∞43∞∞∞∞∞4∞559∞∞∞35∞5∞∞∞5∞55∞7654∞9∞7∞3∞∞∞∞∞63∞2∞∞∞∞5∞2∞6∞∞54∞∞6∞$
$\infty 43 \infty \infty \infty \infty \infty 4 \infty 559 \infty \infty \infty 35 \infty 5 \infty \infty \infty 5 \infty 55 \infty 7654 \infty 9 \infty 7 \infty 3 \infty \infty \infty \infty \infty 63 \infty 2 \infty \infty \infty \infty 5 \infty 2 \infty 6 \infty \infty 54 \infty \infty 6 \infty$ $\begin{matrix} ∞&4&3&∞&∞&∞&∞&∞ \\ 4&∞&5&5&9&∞&∞&∞\\ 3&5&∞&5&∞&∞&∞&5\\ ∞&5&5&∞&7&6&5&4\\ ∞&9&∞&7&∞&3&∞&∞\\ ∞&∞&∞&6&3&∞&2&∞\\ ∞&∞&∞&5&∞&2&∞&6\\ ∞&∞&5&4&∞&∞&6&∞ \end{matrix}$ \right\} $⎩ ⎨ ⎧ \infty 43 \infty \infty \infty \infty \infty 4 \infty 559 \infty \infty \infty 35 \infty 5 \infty \infty \infty 5 \infty 55 \infty 7654 \infty 9 \infty 7 \infty 3 \infty \infty \infty \infty \infty 63 \infty 2 \infty \infty \infty \infty 5 \infty 2 \infty 6 \infty \infty 54 \infty \infty 6 \infty ⎭ ⎬ ⎫$
(2) 邻接表如下所示

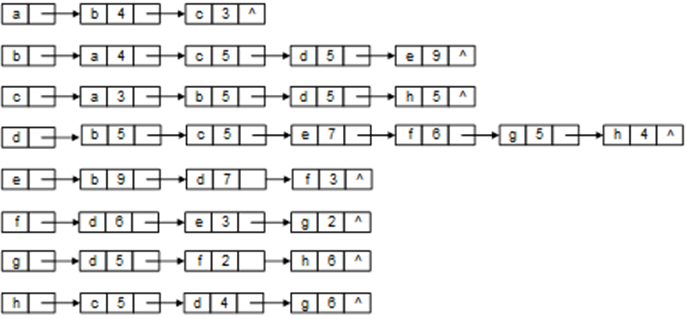
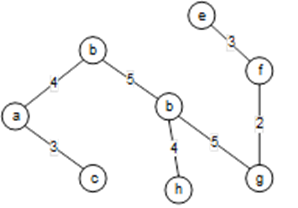
(3) 最小生成树如下所示
参考答案
证明：
假设 $n_0、n_1、n_2$ ，分别是二叉树中度为0，1，2结点的个数。
首先由二叉树的性质可得 $n_0=n_2+1$ 。
又因为二叉树为满二叉树，且有N个结点
则可得 $n_0+n_1+n_2=N$ ， $n_1=0$ ，即 $n_0=N-n_2$
则可得 $2n_0=N+1$ ，即 $n_0 =(N+1)/2$ 。

字母频率	哈夫曼编码	等长二进制编码
0.07	1010	000
0.19	00	001
0.02	10000	010
0.06	1001	011
0.32	11	100
0.03	10001	101
0.21	01	110
0.10	1011	111

二、算法题

参考答案

void Intersection(LinkList &La, LinkList &Lb, LinkList &Lc)
{
    pa=La->next;
    pb=Lb->next;
    Lc=pc=La; 
    while(pa&&pb) 
    {
        if(pa->data==pb->data) 
        {
            pc->next=pa; pc=pa; pa=pa->next; 
            u=pb; pb=pb->next; delete u; 
        }
        else if (pa->data<pb->data)
        {
            u=pa; pa=pa->next; delete u;
        }
        else 
        {
            u=pb; pb=pb->next; delete u;
        }
    }
    while (pa) 
    {
        u=pa; pa=pa->next; delete u;
    }
    while(pb)
    {
        u=pb; pb=pb->next; delete u;
    }
    pc->next=NULL; 
    delete Lb;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

参考答案

void Inverse(LinkList &L)
{
    p=L->next;
    L->next=NULL;
    while(p!=NULL)
    {
        q-p->next; 
        p->next=L->next;
        L->next=p; 
        p=q;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12

参考答案

(1) 算法实现

int IsEqual(int a[m][n],int m,int n)
{   int i,j,k,p;
    for(i=0;i<m;i++)
        for(j=0;j<n-1;j++)
        {
            for(p=j+1;p<n; p++;)//和同行其他元素比较
                if(a[i][j]==a[i][p])//只要有一个相同,则不是互不相同
                {           
                    printf("no");
                    return 0;
                }
            for(k=i+1;k<m;k++)//和第i+1行及以后元素比较
                for(p=0;p<n;p++)
                {
                    if(a[i][j]==a[k][p])
                    printf("no");
                    return 0;
                }   
        }
    printf("yes");
    return 1;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

(2) 算法分析

二维数组中的每一个元素同其他元素都比较一次，数组总计包括m*n个元素，第1个元素同其她m*n-1个元素比较，第2个元素同其它m*n-2个元素比较…第m*n-1个元素同最后一个元素(m*n)比较一次。因此，在元素互不相等的情况下，总的比较次数为:(m*n-1)+(m*n-2)+…+2+1=(m*n)(m*n-1)/2。在存在相同元素的情况下，可能第一次比较时相同，也可能最后一次比较时相同，假设在每个位置上均可能相同，总计包括(m*n-1)个位置，这时的平均比较次数约为(m*n)(m*n-1)/4。因此,算法的时间复杂度是 $O(n^4)$ 。

参考答案

int Level(BiTree T)
{
    num=0;
    if(T)
    {
        InitQueue(Q); 
        EnQueue(Q,T); 
        while(!QueueEmpty(Q))
        {
            DeQueue(Q,p); 
            printf("%d",p->data);//假设值为整数 
            if((p->lchilds&!p->rchild)I1(p->lchild&&p->rchild))
                num++;
            if(p->lchild) EnQueue(Q,p->lchild);
            if(p->rchild) EnQueue(Q,p->rchild);
        }
    }
    return num;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

参考答案

void Process(int a[],int n)
{
    low=0;
    high=n-1;
    while(low<high)
    {
        while(low<high&&a[low]<0)//找到从左向右的非负值记录
            low++;
        while(low<high&&a [high]>0)//找到从右向左的负值记录
            high--;
        if(low<high)//如果需要交换，即low<high
        {
            temp=a[low];
            a[low]=a[high];
            a[high]=temp;//交换记录
            low++;//继续向后找
            high--;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

参考答案

(1) 算法思想

求出各顶点的人度存人数组indegree[i]中，并将人度为0的顶点人栈。
只要栈不空，则重复以下操作:
- 将栈顶顶点vi出栈并保存在拓扑序列数组topo中;
- 对顶点vi的每个邻接点vk的入度减1，如果v的入度变为0，则将vk入栈。
如果输出顶点个数少于AOV网的顶点个数，则网中存在有向环，无法进行拓扑排序，否则拓扑排序成功。

(2) 算法描述

//有向图G采用邻接表存储结构
//若G无回路，则生成c的一个拓扑序列topo[]并返回oK，否则ERROR
Status TopologicalSort (ALGraph G,int topo [ ])
{
    FindInDegree(G,indegree);//求出各顶点的入度存入数组indegree中
    InitStack(S);//栈S初始化为空
    for(i=0;i<G.vexnum;++i)
        if(!indegree[i]) Push(s,i);//入度为0者进栈
    m=O;//对输出顶点计数，初始为0
    while(!StackEmpty(S))//栈s非空
    {
        Pop (s,i);//将栈顶顶点vi出栈
        topo [m]=i;//将vi保存在拓扑序列数组topo中
        ++m;//对输出顶点计数
        p=G.vertices[i].firstarc;//p指向vi的第一个邻接点
        while(p!=NULL)
        {
            k=p->adjvex;//vk为vi的邻接点
            --indegree[k] ;//v;的每个邻接点的入度减1
            if(indegree[k]==O) Push(S,k);//若入度减为0，则入栈
            p=p->nextarc;//p指向顶点vi下一个邻接结点
        }
    }
    if(m<G.vexnum)return ERROR;//该有向图有回路
    else return OK;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

三、补充说明

作者：@江上_酒
扬州大学信息工程学院2022届考研情况分析
 扬州大学858程序设计与数据结构专业课（资料篇）
扬州大学858程序设计与数据结构专业课（编程题篇）

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/IT小白/article/detail/532560