devbox
IT小白
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

2022 第十四届蓝桥杯模拟赛第二期题目题解（比赛时使用方法）_蓝桥杯eda14届模拟赛题二

作者：IT小白 | 2024-05-08 03:51:34

赞

踩

蓝桥杯eda14届模拟赛题二

目录

第一题：最小的2022

第二题：经过天数

第三题：特殊的十六进制数

第四题：矩阵的最小路径

第五题：质数拆分

第六题：拷贝时间

第七题：单词去重

第八题：最短回文串

第九题：多少个X？

第十题：最小交换

第一题：最小的2022

问题描述

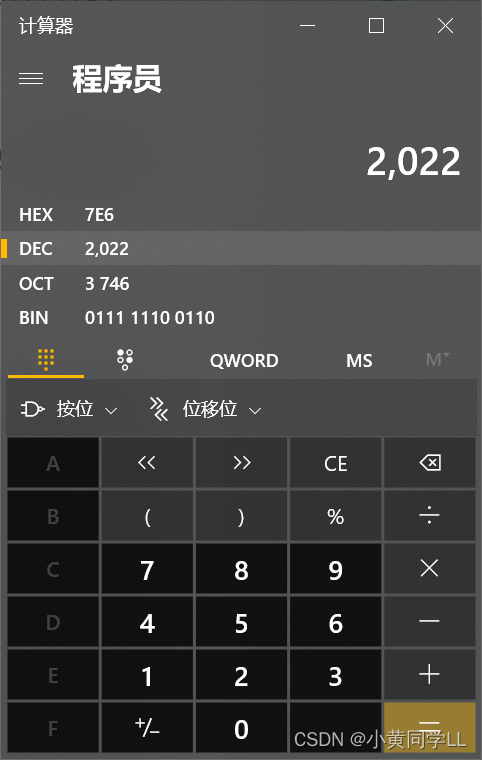
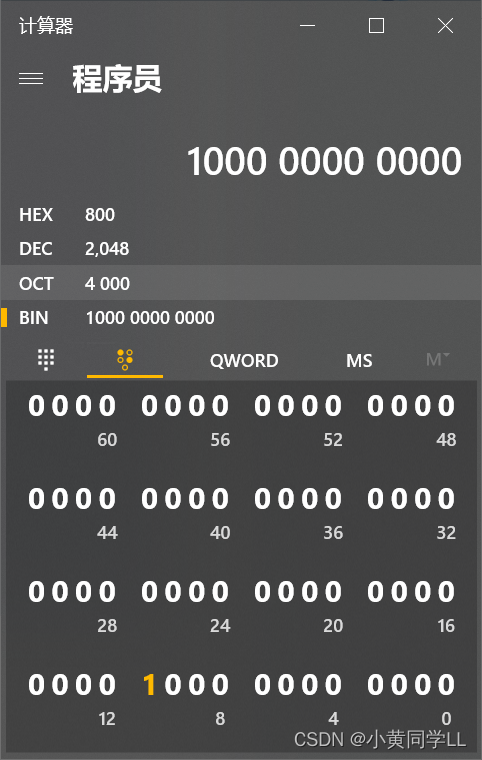
　　请找到一个大于 2022 的最小数，这个数转换成二进制之后，最低的 6 个二进制为全为 0 。
　　请将这个数的十进制形式作为答案提交。

答案提交

　　这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。


 

参考答案：2048

解析：

节约时间，直接打开电脑计算器，输入2022！

很不熟悉计算器的小伙伴可以看看：

HEX ：十六进制 Hexadecimal
DEC ：十进制 Decimal
OCT ：八进制 Octal
BIN ：二进制 Binary

1、MC：清除存储器中的数值。
Memory Clear

2、MR：将存于存储器中的数显示在计算器的显示框上。
Memory Read

3、MS：将显示框的数值存于存储器中。如果存储器中有数值将会显示M标志。
Memory Storage

4、M+：将显示框的数与存储器中的数相加并进行存储。

位
bit: 是计算机内部数据储存的最小单位

字节
Byte: 八个比特 (bit) 称为一个字节,是计算机中数据处理的最基本的单位

字
Word: 两个字节称为一个字, 即16位

双字
Dword: 两个字称为一个双字，两个Word，为32位 D为double

四字
Qword: 两个双字称为一个四字，四个Word，为64位 Q为 quadra

 由题意输入对应二进制，直接看出答案 2048

第二题：经过天数

问题描述

　　我们计从 1949 年 10 月 1 日至 1949 年 10 月 2 日为经过了 1 天。
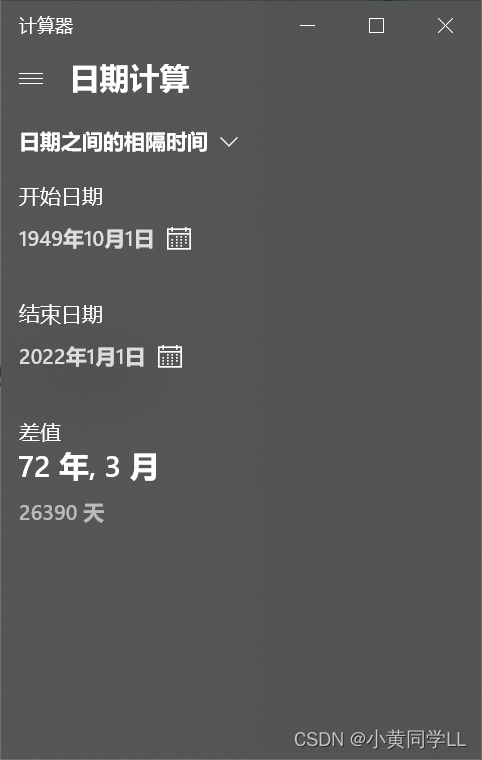
　　请问从 1949 年 10 月 1 日至 2022 年 1 月 1 日经过了多少天？

答案提交

　　这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

参考答案：26390

同样打开计算器！！

比赛时已经结束了，下一题；

复盘暴力代码：

  1. #include <iostream>
  2. #include <cmath>
  3. using namespace std;
  4.  
  5. int leap[12] = {31, 29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
  6.  
  7. int main() {
  8.     int y1 = 1949, m1 = 10, d1 = 1, y2 = 2022, m2 = 1, d2 = 1;
  9.     int ans = 0;
  10.     ans += leap[m1 - 1] - d1;
  11.     for (int i = m1 + 1; i <= 12; i++) {
  12.         ans += leap[i - 1];
  13.     }
  14.     for (int i = y1 + 1; i < y2; i++) {
  15.         if (i % 4 == 0 && i % 100 != 0 || i % 400 == 0) {
  16.             ans += 366;
  17.         } else {
  18.             ans += 365;
  19.         }
  20.     }
  21.     for (int i = 1; i < m2; i++) {
  22.         ans += leap[i - 1];
  23.     }
  24.     ans += d2;
  25.  
  26.     cout << ans << endl;
  27.     return 0;
  28. }

第三题：特殊的十六进制数

问题描述

8518 是一个非常特殊的数，如果把这个数看成 16 进制数，它的值为 (8518)16=8161616+51616+116+8=34072，而 34072 正好是 8518 的整数倍。
9558 也是这样一个数，当看成 16 进制时是 38232。
其实长度为 1 的数 0 到 9 都满足看成 16 进制后是自己的整数倍（1倍）。
请问，除开长度为 1 的数，最小的满足这样条件的数是多少？

答案提交

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

参考答案：1038
 

简单的十六进制转十进制

  1. #include <iostream>
  2. #include <cmath>
  3.  
  4.  
  5. using namespace std;
  6.  
  7. int main() {
  8.     int i = 10;
  9.     while (i<10000) {
  10.         int temp = i;
  11.         int hex = 0;
  12.         int cnt = 0;
  13.         while (temp) {
  14.             hex += temp % 10 * pow(16, cnt);
  15.             temp /= 10;
  16.             cnt++;
  17.         }
  18.         if (hex % i == 0) {
  19.             cout << i <<" "<<hex<<" "<<endl;
  20.             
  21.         }
  22.         i++;
  23.     }
  24.     return 0;
  25. }

取10000范围，可以验证题目示例，保证正确：

第四题：矩阵的最小路径

问题描述

　　小蓝有一个 30 行 60 列的数字矩阵，矩阵中的每个数都是 0 到 9 之间的数字。
　　174094882455171152761423221685761892795431233411387427793198
　　650286024865090061389344606618496378829135984076361542097372
　　601657541200146071777733599818266038012509478351201640618984
　　143988087783837107349651099683484992553337438088068198972282
　　890781586124258626539246182119762952003918195325258677229419
　　698255491250839396799769357665825441616335532825361862146291
　　503649293440596342887581257444442930778730382520372975343211
　　325351222640703400531067500454956482168314849207060705673849
　　265774579830223671554026061117300483012903885770893074783710
　　083450145620356667677191627276513995926532444279237315785832
　　411595106453089134746365281031552217482363035280722591085079
　　053410485925413958279617719034175332412908745680774313630190
　　429314820559328748143552689295945058801322270313370955837837
　　939182801848609300876356583948397645861551964542532682663945
　　625356614462682551015176002433628234343684739800880514363921
　　982340231989891351425389287014819359798014755509282450440511
　　590838726938103384801541373585690893606978941566666714061214
　　952341523168827712604946036245881214982452998386986623826275
　　782780208928205527678781609589000725521486468983551558405472
　　149903035076783644195574734088152324666290493119955560594634
　　905391288186024902215444250421277955403412298227858394469856
　　607272647132163832860126054679347881638761723785858733108109
　　249157334220127702410373959720286708183036202841837581704881
　　367895556630088230650972282944827258473951902831431040790814
　　079538232104075905120989173307660289899942087873076421916033
　　622143260549608274076012938515668898707915863945382394851328
　　164677964192631597026176253407553188801750590935427267220117
　　591817866992665840378311257621611574856498432538327068011953
　　631534031790352912617015229051836886166704989498756486878095
　　690013558017746707412183571476823027885971347137127534455141
　　现在小蓝想从这个矩阵的第一行第一列画一条折线到第 30 行 60 列，线只能沿水平向右走或竖直向下走，只能在有数字的地方拐弯。小蓝想知道，这样一条线经过的数字的和最大是多少。

答案提交

　　这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

参考答案：592


很简单的动态规划题，矩阵中每个点保存到当前这个点的最大路径的和，并依次遍历矩阵更新即可。

  1. 174094882455171152761423221685761892795431233411387427793198
  2. 650286024865090061389344606618496378829135984076361542097372
  3. 601657541200146071777733599818266038012509478351201640618984
  4. 143988087783837107349651099683484992553337438088068198972282
  5. 890781586124258626539246182119762952003918195325258677229419
  6. 698255491250839396799769357665825441616335532825361862146291
  7. 503649293440596342887581257444442930778730382520372975343211
  8. 325351222640703400531067500454956482168314849207060705673849
  9. 265774579830223671554026061117300483012903885770893074783710
  10. 083450145620356667677191627276513995926532444279237315785832
  11. 411595106453089134746365281031552217482363035280722591085079
  12. 053410485925413958279617719034175332412908745680774313630190
  13. 429314820559328748143552689295945058801322270313370955837837
  14. 939182801848609300876356583948397645861551964542532682663945
  15. 625356614462682551015176002433628234343684739800880514363921
  16. 982340231989891351425389287014819359798014755509282450440511
  17. 590838726938103384801541373585690893606978941566666714061214
  18. 952341523168827712604946036245881214982452998386986623826275
  19. 782780208928205527678781609589000725521486468983551558405472
  20. 149903035076783644195574734088152324666290493119955560594634
  21. 905391288186024902215444250421277955403412298227858394469856
  22. 607272647132163832860126054679347881638761723785858733108109
  23. 249157334220127702410373959720286708183036202841837581704881
  24. 367895556630088230650972282944827258473951902831431040790814
  25. 079538232104075905120989173307660289899942087873076421916033
  26. 622143260549608274076012938515668898707915863945382394851328
  27. 164677964192631597026176253407553188801750590935427267220117
  28. 591817866992665840378311257621611574856498432538327068011953
  29. 631534031790352912617015229051836886166704989498756486878095
  30. 690013558017746707412183571476823027885971347137127534455141

可以打印矩阵验证

  1. #include <iostream>
  2. #include <cmath>
  3. using namespace std;
  4.  
  5. int dp[31][61];
  6. char c;
  7.  
  8. int main() {
  9.  
  10.     for (int i = 0; i < 30; i++) {
  11.         for (int j = 0; j < 60; j++) {
  12.             cin >> c;
  13.             dp[i][j] = c - '0';
  14.         }
  15.     }
  16.     cout<<endl;
  17.     for (int i = 0; i < 30; i++) {
  18.         for (int j = 0; j < 60; j++) {
  19.         	if(i&&j)
  20. 				dp[i][j]=dp[i][j]+max(dp[i-1][j],dp[i][j-1]);
  21. 				
  22. 			else if(i==0) dp[i][j]=dp[i][j]+dp[i][j-1];
  23. 			else if(j==0) dp[i][j]=dp[i][j]+dp[i-1][j];
  24. 			
  25.         }
  26.  
  27.         
  28.     }
  29. //        for (int i = 0; i < 30; i++) {
  30. //        	for (int j = 0; j < 60; j++) {
  31. //
  32. //			cout<<dp[i][j]<<" ";
  33. //			
  34. //        }
  35. //        cout<<endl;
  36. //        
  37. //    }
  38.     cout << dp[29][59] << endl;
  39.     return 0;
  40. }

第五题：质数拆分

问题描述

　　将 2022 拆分成不同的质数的和，请问最多拆分成几个？

答案提交

　　这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

 参考答案：33

解析因为才2022，数字不大，可以直接累加然后手算选与不选

  1. #include <iostream>
  2. #include <cmath>
  3. #include <algorithm>
  4.  
  5. using namespace std;
  6.  
  7. int cnt;
  8. int sum;
  9.  
  10.  
  11. bool isPrime(int num) {
  12.     if (num == 1) return false;
  13.     for (int i = 2; i <= sqrt(num); i++) {
  14.         if (num % i == 0) return false;
  15.     }
  16.     return true;
  17. }
  18.  
  19. int main()
  20. {
  21. 	for(int i=1;i<1000;i++)
  22. 	{
  23. 		if(isPrime(i)){
  24. 			sum+=i;
  25. 			cnt++;
  26. 			cout<<i<<" "<<sum<<" "<<cnt<<endl;
  27. 		}
  28. 	}
  29. 	return 0;
  30. }
  1. 质数 总数 个数
  2.  
  3. 2 2 1
  4. 3 5 2
  5. 5 10 3
  6. 7 17 4
  7. 11 28 5
  8. 13 41 6
  9. 17 58 7
  10. 19 77 8
  11. 23 100 9
  12. 29 129 10
  13. 31 160 11
  14. 37 197 12
  15. 41 238 13
  16. 43 281 14
  17. 47 328 15
  18. 53 381 16
  19. 59 440 17
  20. 61 501 18
  21. 67 568 19
  22. 71 639 20
  23. 73 712 21
  24. 79 791 22
  25. 83 874 23
  26. 89 963 24
  27. 97 1060 25
  28. 101 1161 26
  29. 103 1264 27
  30. 107 1371 28
  31. 109 1480 29
  32. 113 1593 30
  33. 127 1720 31
  34. 131 1851 32
  35. 137 1988 33
  36. 139 2127 34

我们发现刚刚好从小到大累加质数就是最长拆分，结束；

第六题：拷贝时间

问题描述

小蓝正在拷贝一份文件，他现在已经拷贝了 t 秒时间，已经拷贝了 c 字节，文件总共有 s 字节，如果拷贝是匀速进行的，请问小蓝大概还需要拷贝多少秒？

输入格式

输入一行包含三个整数 t, c, s，相邻两个整数之间用一个空格分隔。

输出格式

输出一个整数，表示答案。数据保证答案正好是整数。

样例输入1

3 10 20

样例输出1

30 14 21

样例输入2

30 14 21

样例输出2

15

数据范围

对于 50% 的评测用例，1 <= t, c, s <= 10000。

对于所有评测用例，1 <= t, c, s <= 1000000000。

解析：用long long 即可

  1. #include <iostream>
  2. #include <cmath>
  3. using namespace std;
  4.  
  5. typedef long long ll;
  6.  
  7. int main() {
  8.     ll t, c, s;
  9.     cin >> t >> c >> s;
  10.     cout << (s - c) * t / c << endl;
  11.     return 0;
  12. }

第七题：单词去重

问题描述

小蓝有 n 个单词，但是单词中有一些是重复的，请帮小蓝去除重复的单词。

输入格式

输入第一行包含一个正整数 n ，表示小蓝的单词数量。
接下来 n 行，每行包含一个由小写字母组成的单词。

输出格式

请输出去除重复后的那些单词。如果一个单词出现了多遍，请保留第一次出现的单词，去除之后出现的单词，按输入的顺序输出。

样例输入

5
lanqiao
hi
hello
hello
lanqiao

样例输出

lanqiao
hi
hello

评测用例规模与约定

对于所有评测用例， 1<=n<=100，每个单词的长度不超过 100。

用set去重

  1. #include <iostream>
  2. #include <string>
  3. #include <set>
  4.  
  5. using namespace std;
  6.  
  7. typedef long long ll;
  8.  
  9. int main() {
  10.     int n;
  11.     cin >> n;
  12.     set<string> s;
  13.     for (int i = 0; i < n; i++) {
  14.         string temp;
  15.         cin >> temp;
  16.         if (s.find(temp) == s.end()) {
  17.             cout << temp << endl;
  18.             s.insert(temp);
  19.         }
  20.     }
  21.     return 0;
  22. }

第八题：最短回文串

问题描述

　　一个字符串如果从左向右读和从右向左读相同，则称为一个回文串，例如 lanqiaoaiqnal 是一个回文串。
　　小蓝有一个字符串，请将这个字符串右边加上一些字符，使其成为一个回文串。
　　如果有多种方案，请输出最短的回文串。

输入格式

　　输入一行包含一个字符串，由小写英文字母组成。

输出格式

　　输出一行包含答案。

样例输入

lanqiao

样例输出

lanqiaoaiqnal

样例输入

banana

样例输出

bananab

样例输入

noon

样例输出

noon

评测用例规模与约定

　　对于所有评测用例，1 <= 字符串长度 <= 100。

枚举字符串中最长的回文后缀即可，枚举出来后，此时的前缀（可能为空）进行反转后就是应当加在最开始字符串的后面，输出答案即可。 

  1. #include <iostream>
  2. #include <cstring>
  3. #include <algorithm>
  4.  
  5. using namespace std;
  6.  
  7. int n;
  8. string s;
  9.  
  10. bool check(string s)
  11. {
  12. 	int i = 0, j = s.size() - 1;
  13. 	while (i < j)
  14. 		if (s[i++] != s[j--])
  15. 			return false;
  16. 	return true;
  17. }
  18.  
  19. int main()
  20. {
  21. 	cin >> s;
  22.  
  23. 	n = s.size();
  24. 	for (int i = 0, len = n; i < n; i++, len--)
  25. 	{
  26. 		string t = s.substr(i, len);//找到最长回文串
  27. 		if (check(t))
  28. 		{
  29. 			string prev = s.substr(0, i);
  30. 			string post = prev;
  31. 			if (prev.size())
  32. 			{
  33. 				reverse(post.begin(), post.end());
  34. 				cout << prev + t + post << endl;
  35. 				return 0;
  36. 			}
  37. 			else
  38. 			{
  39. 				cout << t << endl;
  40. 				return 0;
  41. 			}
  42. 		}
  43. 	}
  44. 	return 0;
  45. }

第九题：多少个X？

问题描述

　　给定一个字母矩阵。一个 X 图形由中心点和由中心点向四个45度斜线方向引出的直线段组成，四条线段的长度相同，而且四条线段上的字母和中心点的字母相同。
　　一个 X图形可以使用三个整数 r, c, L 来描述，其中 r, c 表示中心点位于第 r 行第 c 列，正整数 L 表示引出的直线段的长度。 对于 1 到 L 之间的每个整数 i，X图形满足：第 r-i 行第 c-i 列与第 r 行第 c 列相同，第 r-i 行第 c+i 列与第 r 行第 c 列相同，第 r+i 行第 c-i 列与第 r 行第 c 列相同，第 r+i 行第 c+i 列与第 r 行第 c 列相同。
　　例如，对于下面的字母矩阵中，所有的字母 L 组成一个 X图形，其中中间的 5 个 L 也组成一个 X图形。所有字母 Q 组成了一个 X图形。
　　LAAALA
　　ALQLQA
　　AALQAA
　　ALQLQA
　　LAAALA
　　给定一个字母矩阵，请求其中有多少个 X图形。

输入格式

　　输入第一行包含两个整数 n, m，分别表示字母矩阵的行数和列数。
　　接下来 n 行，每行 m 个大写字母，为给定的矩阵。

输出格式

　　输出一行，包含一个整数，表示答案。

样例输入

5 6
LAAALA
ALQLQA
AALQAA
ALQLQA
LAAALA

样例输出

3

评测用例规模与约定

　　对于 50% 的评测用例，1 <= n, m <= 10。
　　对于所有评测用例，1 <= n, m <= 100。

暴力模拟

  1. #include <iostream>
  2. #include <cmath>
  3. #include <vector>
  4.  
  5.  
  6. using namespace std;
  7.  
  8. typedef long long ll;
  9.  
  10. int main() {
  11.     int n, m;
  12.     cin >> n >> m;
  13.     vector<string> matrix;
  14.     for (int i = 0; i < n; i++) {
  15.         string s;
  16.         cin >> s;
  17.         matrix.push_back(s);
  18.     }
  19.     int ans = 0;
  20.     for (int i = 1; i < n - 1; i++) {
  21.         for (int j = 1; j < m - 1; j++) {
  22.             int cnt = 1;
  23.             while (i - cnt >= 0 && i + cnt < n && j - cnt >= 0 && j + cnt < m &&
  24.                 matrix[i + cnt][j + cnt] == matrix[i][j] && matrix[i + cnt][j - cnt] == matrix[i][j] &&
  25.                 matrix[i - cnt][j + cnt] == matrix[i][j] && matrix[i - cnt][j - cnt] == matrix[i][j]) {
  26.                 cnt++;
  27.             }
  28.             ans += (cnt - 1);
  29.         }
  30.     }
  31.     cout << ans << endl;
  32.     return 0;
  33. }

第十题：最小交换

问题描述

　　小蓝有一个序列 a[1], a[2], ..., a[n]，每次可以交换相邻的两个元素，代价为两个元素中较大的那个。
　　请问，要通过交换将序列变为从小到大递增的序列，总代价最少为多少？

输入格式

　　输入一行包含一个整数 n ，表示序列长度。
　　第二行包含 n 个整数，表示给定的序列。

输出格式

　　输出一行包含一个整数，表示最少代价的值。

样例输入

4
1 5 2 1

样例输出

12

评测用例规模与约定

　　对于 30% 的评测用例，1 <= n <= 1000, 1 <= a[i] <= 1000。
　　对于 60% 的评测用例，1 <= n <= 50000, 1 <= a[i] <= 50000。
　　对于所有评测用例，1 <= n <= 1000000, 1 <= a[i] <= 1000000。

 解析：

我的想法是这样的，因为升序后的排列数值都是一样的，那么只需要找到让数组升序的最小操作数即可，即求逆序对数，过程中累加最大值；

  1. #include <iostream>
  2. #include <cmath>
  3. #include <algorithm>
  4.  
  5. using namespace std;
  6.  
  7. const int N=1000010;
  8. int a[N];
  9. int main()
  10. {
  11. 	int n,sum=0,temp;
  12. 	scanf("%d",&n);
  13.  
  14. 	for(int i=0;i<n;i++){
  15. 		scanf("%d",&a[i]);
  16. 	}
  17. 	for(int i=0;i<n-1;i++){
  18. 		for(int j=i+1;j<n;j++){
  19. 			if(a[i]>a[j]){
  20. 				temp=a[i];
  21. 				a[i]=a[j];
  22. 				a[j]=temp;
  23. 				sum+=temp;
  24. 			}
  25. 		}
  26. 	}
  27. 	printf("%d\n",sum);
  28. 	return 0;
  29. }
  30.

 

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/IT小白/article/detail/552678
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号