Llama模型结构解析（源码阅读）_llama结构

• 参考资料：
  https://zhuanlan.zhihu.com/p/636784644
  https://spaces.ac.cn/archives/8265 ——《Transformer升级之路：2、博采众长的旋转式位置编码》

前言：本次阅读代码位置，在transformers库底下的modeling_llama.py，具体位置在：transformers/models/llama/modeling_llama.py，如下图所示：

1. LlamaModel整体结构流程图

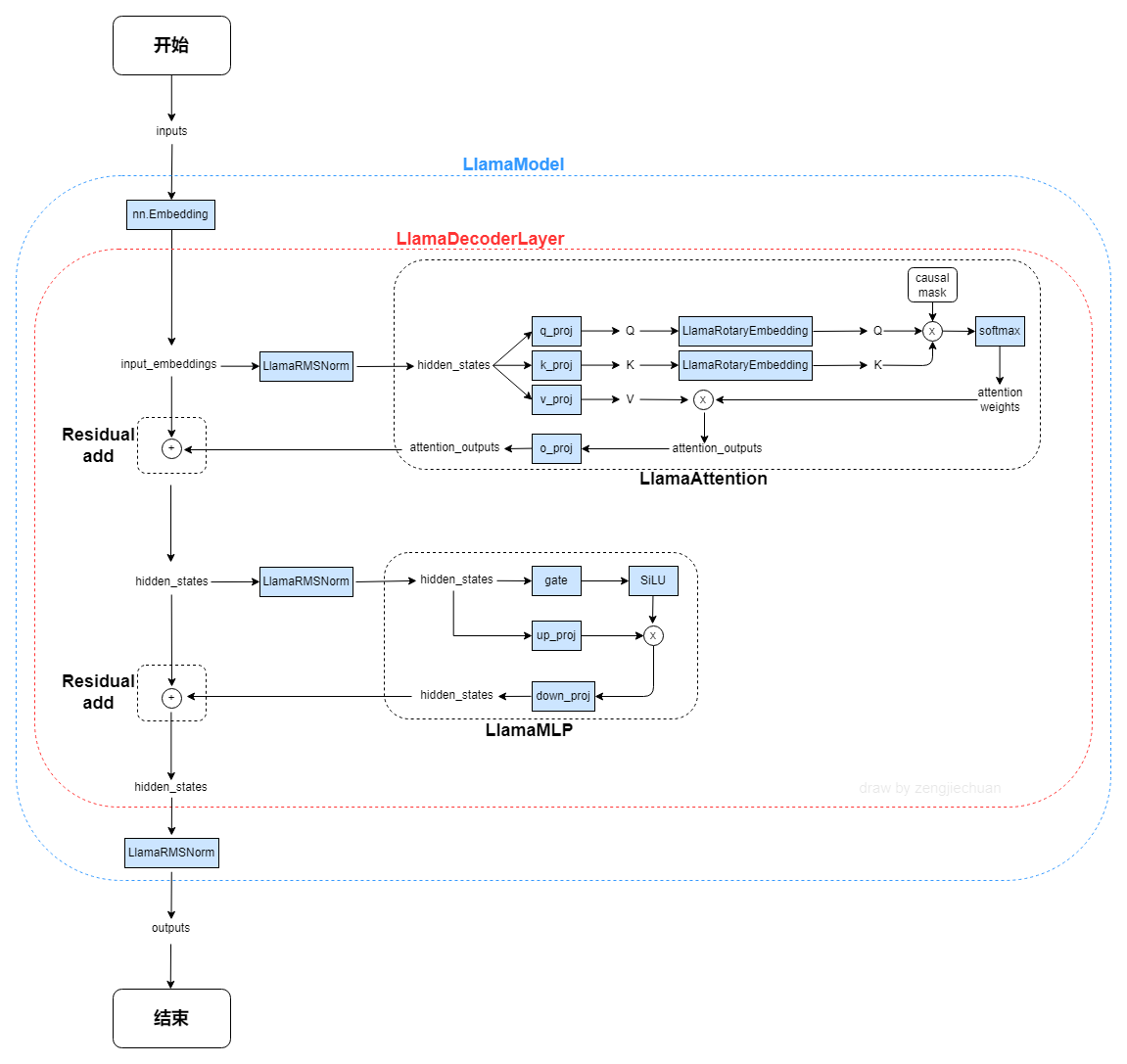
2. LlamaRMSNorm

• 代码如下

class LlamaRMSNorm(nn.Module):
    def __init__(self, hidden_size, eps=1e-6):
        """
        LlamaRMSNorm is equivalent to T5LayerNorm
        """
        super().__init__()
        self.weight = nn.Parameter(torch.ones(hidden_size))
        self.variance_epsilon = eps

    def forward(self, hidden_states):
        input_dtype = hidden_states.dtype
        variance = hidden_states.to(torch.float32).pow(2).mean(-1, keepdim=True)
        hidden_states = hidden_states * torch.rsqrt(variance + self.variance_epsilon)

        return (self.weight * hidden_states).to(input_dtype)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

• RMSNorm的公式如下所示：
  $\frac{x_i}{\sqrt{\frac{1}{n}\sum _{i=1}^n{x_i}^2+eps}}\ast weigh{t}_i$

  • 其中，公式与代码的对应关系如下：
    

3. LlamaMLP

• 代码如下：

class LlamaMLP(nn.Module):
    def __init__(
        self,
        hidden_size: int,
        intermediate_size: int,
        hidden_act: str,
    ):
        super().__init__()
        self.gate_proj = nn.Linear(hidden_size, intermediate_size, bias=False)
        self.down_proj = nn.Linear(intermediate_size, hidden_size, bias=False)
        self.up_proj = nn.Linear(hidden_size, intermediate_size, bias=False)
        self.act_fn = ACT2FN[hidden_act]

    def forward(self, x):
        return self.down_proj(self.act_fn(self.gate_proj(x)) * self.up_proj(x))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

• 流程图：
  

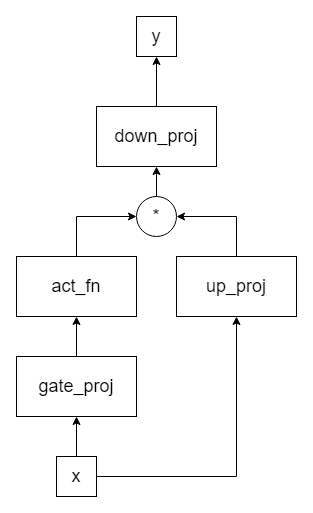
• 其中输入为x，输出为y

• 代码中intermediate_size一般比hidden_size大，我们通过在jupyter notebook中打印Llama-13B的模型，可以看到如下所示：
  

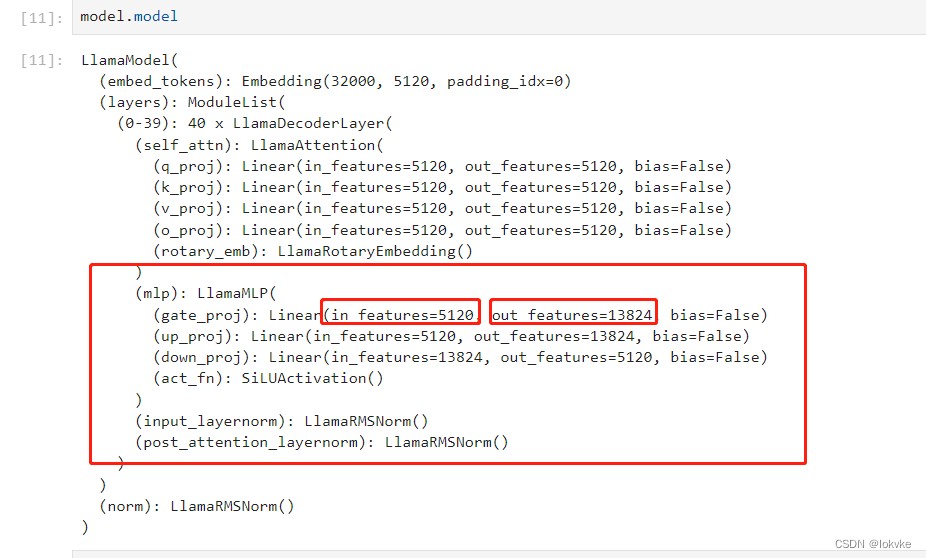
• 总结：MLP模块就是几个nn.Linear的组合

4. LlamaRotaryEmbedding

• 代码如下

class LlamaRotaryEmbedding(torch.nn.Module):
    def __init__(self, dim, max_position_embeddings=2048, base=10000, device=None):
        super().__init__()
        inv_freq = 1.0 / (base ** (torch.arange(0, dim, 2).float().to(device) / dim))
        self.register_buffer("inv_freq", inv_freq)

        # Build here to make `torch.jit.trace` work.
        self.max_seq_len_cached = max_position_embeddings
        t = torch.arange(self.max_seq_len_cached, device=self.inv_freq.device, dtype=self.inv_freq.dtype)
        freqs = torch.einsum("i,j->ij", t, self.inv_freq)
        # Different from paper, but it uses a different permutation in order to obtain the same calculation
        emb = torch.cat((freqs, freqs), dim=-1)
        self.register_buffer("cos_cached", emb.cos()[None, None, :, :], persistent=False)
        self.register_buffer("sin_cached", emb.sin()[None, None, :, :], persistent=False)

    def forward(self, x, seq_len=None):
        # x: [bs, num_attention_heads, seq_len, head_size]
        # This `if` block is unlikely to be run after we build sin/cos in `__init__`. Keep the logic here just in case.
        if seq_len > self.max_seq_len_cached:
            self.max_seq_len_cached = seq_len
            t = torch.arange(self.max_seq_len_cached, device=x.device, dtype=self.inv_freq.dtype)
            freqs = torch.einsum("i,j->ij", t, self.inv_freq)
            # Different from paper, but it uses a different permutation in order to obtain the same calculation
            emb = torch.cat((freqs, freqs), dim=-1).to(x.device)
            self.register_buffer("cos_cached", emb.cos()[None, None, :, :], persistent=False)
            self.register_buffer("sin_cached", emb.sin()[None, None, :, :], persistent=False)
        return (
            self.cos_cached[:, :, :seq_len, ...].to(dtype=x.dtype),
            self.sin_cached[:, :, :seq_len, ...].to(dtype=x.dtype),
        )
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

• 具体的使用，还调用了另外两个函数，如下所示：

def rotate_half(x):
    """Rotates half the hidden dims of the input."""
    x1 = x[..., : x.shape[-1] // 2]
    x2 = x[..., x.shape[-1] // 2 :]
    return torch.cat((-x2, x1), dim=-1)


def apply_rotary_pos_emb(q, k, cos, sin, position_ids):
    # The first two dimensions of cos and sin are always 1, so we can `squeeze` them.
    cos = cos.squeeze(1).squeeze(0)  # [seq_len, dim]
    sin = sin.squeeze(1).squeeze(0)  # [seq_len, dim]
    cos = cos[position_ids].unsqueeze(1)  # [bs, 1, seq_len, dim]
    sin = sin[position_ids].unsqueeze(1)  # [bs, 1, seq_len, dim]
    q_embed = (q * cos) + (rotate_half(q) * sin)
    k_embed = (k * cos) + (rotate_half(k) * sin)
    return q_embed, k_embed
    
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

• 注意这里的实现跟原始推导有点区别，这里实现的方式如下图所示：
  

• 原始推导如下图所示：
  
  具体可以查看作者的博客：

  声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/Monodyee/article/detail/662520