线性表（linear list）是n个具有相同特性的数据元素的有限序列。线性表是一种在实际中广泛使用的数据结构，常见的线性表：顺序表、链表、栈、队列、字符串...

线性表在逻辑上是线性结构，也就说是连续的一条直线。但是在物理结构上并不一定是连续的，线性表在物理上存储时，通常以数组和链式结构的形式存储。

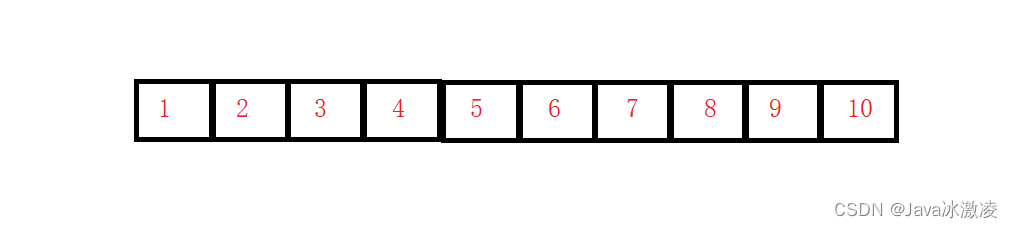
二、顺序表

顺序表是用一段物理地址连续的存储单元依次存储数据元素的线性结构，一般情况下采用数组存储。在数组上完成数据的增删查改

顺序表一般可以分为：
静态顺序表：使用定长数组存储。
动态顺序表：使用动态开辟的数组存储。（malloc）
静态顺序表适合用于已知需要存多少数据的场景，静态顺序表会导致空间开辟过大，造成空间浪费，或空间开辟过小，导致内存不够使用

相比之下使用动态顺序表更加的灵活

首先我们来使用代码定义一个静态的顺序表看看

1.定义顺序表类


 public class SeqList {
    public int[] elem;
    public int elemSize;
    public  SeqList(){
        this.elem=new int[10];
    }

代码分析：

首先定义了SeqList类代表顺序表

在类中设置了数组elem elseSize用来存储顺序表已有的元素个数

接下来我们要实现一些顺序表的基本功能

public void dispplay（）{}//打印顺序表

public void add（int pos，int date）{}//在pos位置新增元素

public boolean contains(int toFind) { return true; }// 判定是否包含某个元素
public int search(int toFind) { return -1; }// 查找某个元素对应的位置
public int getPos(int pos) { return -1; }// 获取 pos 位置的元素
public void setPos（int pos，int value）{}//将pos位置的值置为value

public void remove（int Remove）{}//删除第一次出现的关键字

public int size（）{}//获取顺序表长度

public void clear（）{}//清空顺序表

下面我们来代码实现一下

2.功能实现：

打印顺序表


// 打印顺序表
    public void display() {
        for (int i = 0; i <this.elemSize ; i++) {
            System.out.print(elem[i]+" ");
        }
        System.out.println();
    }

代码分析：

elemSize中存储的是元素的个数，所以其余正常打印就ok

在pos位置新增元素


    // 在 pos 位置新增元素
    public void add(int pos, int data) {
        //1.判断pos位置的合法性
        if(pos<0||pos>this.elemSize){
            System.out.println("pos 位置不合法");
            return;
        }
        //2.如果存放大小不够进行扩容
        if(ispos(pos)){
            this.elem=Arrays.copyOf(this.elem,this.elem.length*2);
        }
        //3.移动元素
        for (int i = this.elemSize-1; i >pos ; i--) {
                elem[i+1]=elem[i];
        }
        this.elem[pos]=data;
        this.elemSize++;
    }
    //判断是否需要扩容
    public boolean ispos(int pos){
        if(this.elemSize==pos){
            return true;
        }
        return false;
    }

代码分析：

我们要先将问题开始进行拆分

        首先我们要考虑到pos位置下标是否合法，在顺序表中有规定，必须依次存放，所以要先判断pos下标的合法性

        之后要考虑到，如果pos的位置是合法的，但是如果开辟的空间不够使用的话，我们就要进行相应的扩容

        其次如果已经要存放的pos位置已有元素，那么我们需要将pos位置以及后面所有元素进行后移以便于存放data元素

最后我们要考虑到，在新添加元素后 elemSize存放的为总个数，所以切记一定要使elemSize++

判定是否包含某个元素


// 判定是否包含某个元素
    public boolean contains(int toFind) {
        for (int i = 0; i <this.elemSize ; i++) {
            if(this.elem[i]==toFind){
                return true;
            }
        }
        return false; }

代码分析：

这个操作非常简单，遍历顺序表一次查找是否存在即可

查找某个元素对应的位置


 // 查找某个元素对应的位置
    public int search(int toFind) {
        for (int i = 0; i <this.elemSize ; i++) {
            if(this.elem[i]==toFind){
                return i;
            }
        }
        System.out.println("没有找到对应元素");
        return -1; }
    // 获取 pos 位置的元素

代码分析：

此操作也是跟查找元素是否存在同理

获取pos位置的元素


 // 获取 pos 位置的元素
    public int getPos(int pos) {
        if(pos>=0&&pos<=this.elemSize){
            return this.elem[pos];
        }
        System.out.println("下标元素不合法");
        return -1; }

代码分析：

首先我们要考虑到pos的位置的合法性，如果合法可直接返回位置对应的元素

给 pos 位置的元素设为 value


// 给 pos 位置的元素设为 value
    public void setPos(int pos, int value) {
        if(pos<0||pos>=this.elemSize){
            System.out.println("坐标不合法");
            return;
        }
        this.elem[pos]=value;
 
    }

代码分析：

首先我们还是要先考虑到位置的合法性，如果合法直接修改值即可

删除第一次出现的关键字key


 //删除第一次出现的关键字key
    public void remove(int toRemove) {
        for (int i = 0; i <this.elemSize ; i++) {
            if(this.elem[i]==toRemove){
                for (int j = i; j <this.elemSize-1 ; j++) {
                    this.elem[i]=this.elem[i+1];
                }
                this.elemSize--;
                return;
            }
        }
 
    }

代码分析：

我们先来遍历顺序表一次来找到是否出现了key元素并且找到其下标，随之将之后元素依次覆盖到前面，之后切记elemSize--；代表最后一个元素直接被抛弃了，因为elemSize存储的是元素个数

获取顺序表的长度


 // 获取顺序表长度
    public int size() {
        if(this.elemSize>0){
            return this.elemSize;
        }
        return 0; }

代码分析：

判断如果elemSize中不为0则代表已有元素，则返回elemSize长度，其实可以直接来返回elemSize元素个数，但是顺序表是非常严谨的，所以我们需要将代码写得严谨

清空顺序表


// 清空顺序表
    public void clear() {
        this.elemSize=0;
    }

代码分析：

我们在之前的代码实现中发现了elemSize是存储的元素的个数，所以我们可以直接通过修改elemSize的值来达到清空顺序表

总结

总归来说我们的顺序表的实现类似于数组，所以学习起来也是非常的简单，但是需要注意到的是，由于顺序表的严谨程度，我们在实现功能的时候需要更多的考虑严谨性，例如判断其下标的合法性，以及每次进行完操作后都需要修改其elemSize的值

三、链表

链表概念、结构

链表是一种物理存储结构上非连续存储结构，数据元素的逻辑顺序是通过链表中的引用链接次序实现的

实际中链表的结构非常多样，以下情况组合起来就有8种链表结构：
单向、双向
带头、不带头
循环、非循环

首先来解释一下单向跟双向的区别，单向代表链表元素只存储了下一个元素的位置或者只存储了上一个元素的位置，所以只能依次向后访问或者向前访问

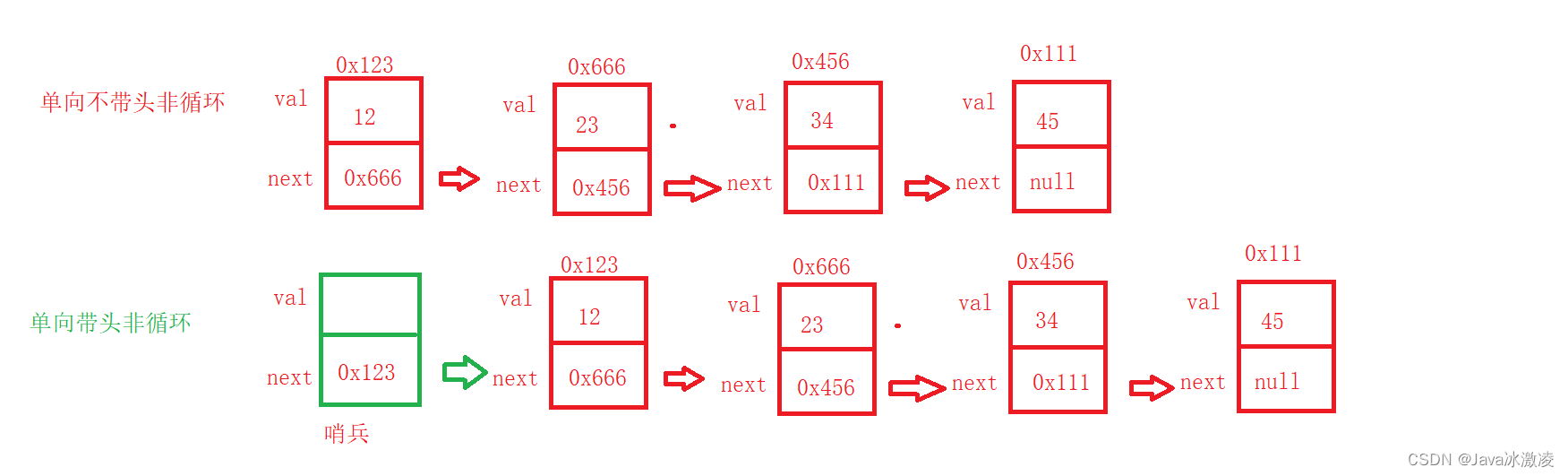
带头不带头是什么意思呢，如果带头我们可以理解为链表前面有一个哨兵，一张图供大家理解

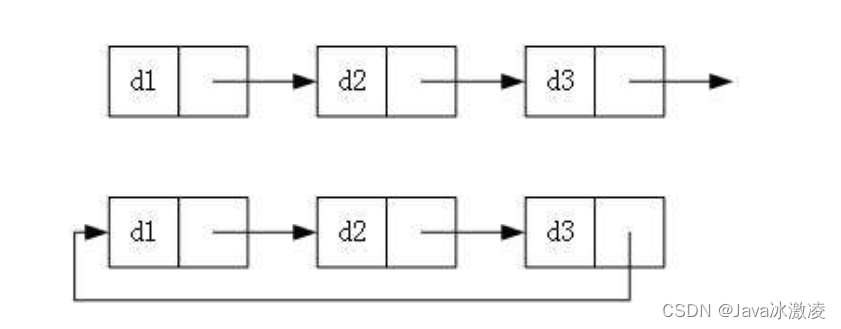
循环和非循环的意思是在链表中是否会有循环，如果有循环的话可以理解为这个链表是没有末尾的

虽然有这么多的链表的结构，但是我们重点掌握两种:
无头单向非循环链表：结构简单，一般不会单独用来存数据。实际中更多是作为其他数据结构的子结构，如哈希桶、图的邻接表等等。另外这种结构在笔试面试中出现很多。

无头双向链表：在Java的集合框架库中LinkedList底层实现就是无头双向循环链表

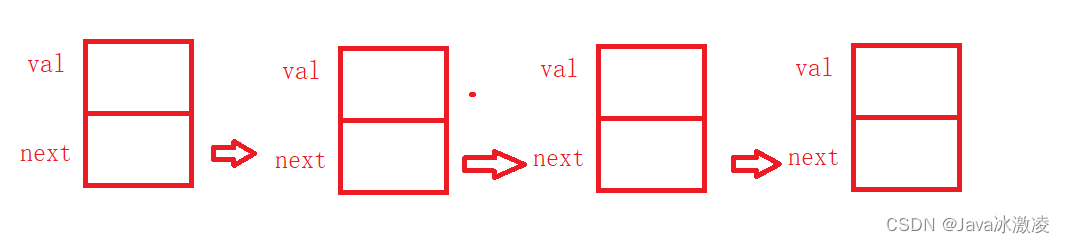
链表实现类


/**
 * /不带头单向链表
 */
class ListNode {
    public int val;
    public ListNode next;
 
    public ListNode(int val){
        this.val=val;
    }
}

代码分析：

定义了类名为ListNode的链表，val用来存放值，next存放的为下一个位置的地址或者上一个位置的地址

我们还是先来实现一下基本链表的功能
public void addFirst(int data);//头插法
public void addLast(int data);//尾插法
public boolean addIndex(int index,int data);//任意位置插入,第一个数据节点为0号下标
public boolean contains(int key);//查找是否包含关键字key是否在单链表当中
public void remove(int key);//删除第一次出现关键字为key的节点
public void removeAllKey(int key);//删除所有值为key的节点
public int size();//得到单链表的长度
public void display();//输出链表的值
public void clear();//清空链表

初始化链表


    public void Listeag() {
        //初始化链表中的值
        ListNode listNode1 = new ListNode(12);
        ListNode listNode2 = new ListNode(23);
        ListNode listNode3 = new ListNode(34);
        ListNode listNode4 = new ListNode(23);
        ListNode listNode5 = new ListNode(56);
 
        //串联链表 现在链表中的next都为null
        listNode1.next = listNode2;
        listNode2.next = listNode3;
        listNode3.next = listNode4;
        listNode4.next = listNode5;
        head=listNode1;
        //listNode5.next不需要
    }

代码分析：

我们先来简单的初始化一下链表，还要做到串联一下链表，其中最后一个的next存储为null，null表示为链表的结尾

头插法


//头插法
    public void addFirst(int data){
        ListNode red=new ListNode(data);
        if(this.head==null){
            this.head=red;
        }else{
            red.next=this.head;
            this.head=red;
        }
    }

代码分析：

首先我们需要new出一个对象节点来存储data的值并且将head首个节点的地址取出存放到red.next中，之后将red置为链表的头部就实现了头插法

尾插法


 //尾插法
    public void addLast(int data){
        if(head==null){
            addFirst(data);
        }else {
            ListNode red=head;
            while(red.next!=null){
                red=red.next;
            }
            ListNode flg=new ListNode(data);
            red.next=flg;
 
        }

代码分析：

首先我们秉着严谨性来判断链表是否为空，如果链表为空的话可以直接调用头插法来插入，不为空的话我们需要遍历找到链表最后一个节点，将next修改为新new出的节点的地址来达到串联的效果（由于新new出的节点next都为null，所以可以不处理）

任意位置插入,第一个数据节点为0号下标


 //任意位置插入,第一个数据节点为0号下标
    public void addIndex(int index,int data){
        if(index<0||index>size()){
            System.out.println("index下标不合法！插入失败！");
            return ;
        }
        if(index==0){
            addFirst(data);
        }
        if(size()==index){
            addLast(data);
        }
        ListNode red=this.head;
        while(index-1>0){
            red=red.next;
            index--;
        }
        ListNode flg=new ListNode(data);
        flg.next=red.next;
        red.next=flg;
 
    }

代码分析：

首先还是要先来判断下标的合法性，再判断要插入的下标是否为头或者尾，如果是头或者尾可以相应来调用头插法或者尾插法，否则的话我们需要来进行插入，即是获取到要插入位置之前的next修改为新节点的地址，新节点的next修改为下一个节点的地址；

简单的实现可以先使新节点的next得到前一个节点的next，再修改之前的next的地址即可少开辟一个空间

查找是否包含关键字key


 //查找是否包含关键字key是否在单链表当中
    public boolean contains(int key){
        ListNode red=this.head;
        while(red.next!=null){
            if(red.val==key){
                return true;
            }
            red=red.next;
        }
        return false;
    }

代码分析：

我们先将链表进行遍历取出每个节点的val来比较，如果链表走到null还未找到有相等的，则不包含关键字key，返回false

删除第一次出现关键字为key的节点


//删除第一次出现关键字为key的节点
    public void remove(int key){
        if(this.head==null){
            System.out.println("单链表为空，不能删除！");
            return ;
        }
        if(this.head.val==key){
            this.head=this.head.next;
            return ;
        }
        ListNode red=this.head;
        while(red.next!=null){
            if(red.next.val==key){
                red.next=red.next.next;
                return ;
            }
            red=red.next;
        }
    }

代码分析：

先来判断链表是否为空，再先考虑头节点是否为要被删除的节点，然后我们再依次遍历链表来寻找是否存在需要被删除的节点，如果找到需要被删除的节点，我们可以直接将上一个节点的next变为要被删除的节点的next，删除一次即可

删除所有值为key的节点


//删除所有值为key的节点
    public void removeAllKey(int key){
        if(this.head==null) return ;
        ListNode del=this.head;
        ListNode cur=del.next;
        while(cur!=null){
            if(cur.val==key){
                del.next=cur.next;
                cur=cur.next;
            }
            else {
                del=cur;
                cur=cur.next;
            }
        }
        //处理头节点
        if(this.head.val==key){
            head=head.next;
        }
    }

代码分析：

有的同学已经想到了，可以多次调用删除第一个出现key节点函数来实现删除，我们也可以进入链表遍历进行寻找，原理和删除第一个出现key节点函数实现一样，最后记得处理头节点

得到单链表的长度


//得到单链表的长度
    public int size(){
        int count =0;
        ListNode flg=this.head;
        while(flg!=null){
            count++;
            flg=flg.next;
        }
        return count;
    }

代码分析：

我们设置一个count来存放节点的个数，依次遍历链表，当节点==null代表走到了链表最后，随之跳出循环返回count

清空链表


//清空链表
public void clear(){
        //粗暴做法
        //this.head=null;
        //温柔做法
        ListNode tur=this.head.next;
        while(this.head!=null){
            this.head.next=null;
            this.head=tur;
            tur=tur.next;
        }
    }

代码分析：

我们有两种方法，第一种就是暴力解法了，我们可以直接使头节点变为null，但是我们使用粗暴做法有一个瑕疵，清空链表的初衷是为了释放被链表所占的内存，我们这么操作是不会使链表都释放的

第二种解法是依次遍历链表将每个节点都置位null，这样即可达到释放链表且清空链表

以上就是单向链表的功能的实现，双向链表的实现原理是近似的

四、链表面试题

1. 删除链表中等于给定值 val 的所有节点。OJ链接
2. 反转一个单链表。OJ链接
3. 给定一个带有头结点 head 的非空单链表，返回链表的中间结点。如果有两个中间结点，则返回第二个中间结点。OJ链接
4. 输入一个链表，输出该链表中倒数第k个结点。OJ链接
5. 将两个有序链表合并为一个新的有序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。OJ链接
6.在一个排序的链表中，存在重复的结点，请删除该链表中重复的结点，重复的结点不保留，返回链表头指针。OJ链接
7.链表的回文结构。OJ链接

8.输入两个链表，找出它们的第一个公共结点。OJ链接

9.给定一个链表，判断链表中是否有环。OJ链接

10.给定一个链表，返回链表开始入环的第一个节点。OJ链接

删除链表中等于给定值 val 的所有节点


public ListNode removeElements(ListNode head, int val) {
        if(head==null)return null;
        ListNode red=head;
        ListNode del=head.next;
        while(del!=null){
            if(del.val==val){
                del=del.next;
            }else {
                red.next=del;
                del=del.next;
                red=red.next;
            }
 
        }
        red.next=null;
        //处理头节点
        if(head.val==val){
            head=head.next;
        }
        return head;
    }

代码分析：

这个思路我们之前在实现链表基本功能已经实现过，首先我们需要两个引用来访问head与head.next，每次循环判断head.next.val，如果不为要删除的值那么后移一位，如果为要被删除的节点，则将del.next赋给red.next,随后再都后移，最后判断一下头节点即可，有一个需要注意到的点是最后要将red.next=null，因为最后一位咱们不能确定是不是要被删除的节点

反转一个单链表


class Solution {
    public ListNode reverseList(ListNode head) {
        if(head==null)return head;
       ListNode cur=head;
       ListNode tmp=cur.next;
       while(tmp!=null){
           ListNode tmpNext=tmp.next;
           tmp.next=cur;
           cur=tmp;
           tmp=tmpNext;
       }
       //处理头节点
       head.next=null;
       return cur;
    }
}

代码分析：

以上PDF是它的交换过程 ,最后我们需要格外注意不要造成空引用访问，最后处理一下头节点就ok啦，将head.next置为null

返回链表的中间结点


class Solution {
    public ListNode middleNode(ListNode head) {
        if(head==null){
            return null;
        }
          ListNode del=head;
          ListNode shor=head;
        while(shor!=null&&shor.next!=null){
            
            shor=shor.next.next;
            del=del.next;
        }
           return del;
    }
}

代码分析：

我们定义了两个引用，一个快引用每次移动两个节点，另一个慢引用一次移动一个节点，那么当快引用==null时，我们的慢引用就会刚好走到中间

输入一个链表，输出该链表中倒数第k个结点


public class Solution {
    public ListNode FindKthToTail(ListNode head, int k) {
        if (k <= 0 || head == null) {
            return null;
        }
        ListNode red = head;
        ListNode del = head;
        while (k - 1 > 0 ) {
 
            red = red.next;
            if (red == null) {
                return null;
            }
            k--;
        }
        while (red.next != null) {
            red = red.next;
            del = del.next;
        }
        return del;
    }
    public int size(ListNode head) {
        int count = 0;
        ListNode red = head;
        while (red != null) {
            red = red.next;
            count++;
        }
        return count;
    }
}

代码分析：

定义两个引用，都从头开始，先将其中一个移动倒数几位就移动几位，之后再两个引用一起开始每次移动一位，当先移动的引用到达链表末尾则后移动的引用为要找的位置

将两个有序链表合并为一个新的有序链表并返回


class Solution {
    public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
        ListNode newHead=new ListNode();
        ListNode red=newHead;
        while(list1!=null&&list2!=null){
            if(list1.val<list2.val){
                red.next=list1;
                list1=list1.next;
                red=red.next;
            }
            else {
                red.next=list2;
                list2=list2.next;
                red=red.next;
            }
        }
        if(list1!=null){
            red.next=list1;
        }
        else if(list2!=null){
            red.next=list2;
        }
        return newHead.next;
    }
}

代码分析：

已知第一个链表和第二个链表都为有序，则可以新开辟一个链表用来存放新链表，将之后合并的拼接在newHead.next后，首先将第一个链表中第一位与第二个链表第一位进行判断，将小的放入新链表中，并且向后移动一位，当一个链表结束时，判断没有到最后的链表直接跟随到新链表后面即可

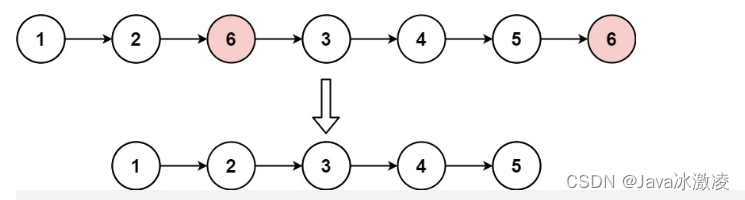
在一个排序的链表中，存在重复的结点，请删除该链表中重复的结点


public class Solution {
    public ListNode deleteDuplication(ListNode head) {
       //
        ListNode cur = head;
        ListNode newHead = new ListNode(1);
        ListNode tmp = newHead;
        while (cur != null ) {
            if (cur.next != null && cur.val == cur.next.val) {
                while (cur != null && cur.next != null && cur.val == cur.next.val) {
                    cur = cur.next;
                }
                cur = cur.next;
            } else {
                tmp.next = cur;
                tmp = tmp.next;
                cur = cur.next;
            }
        }
        tmp.next = null;
        return newHead.next;
    }
}

代码分析：

一个引用指向链表开头，另一个引用指向开头节点下一位，判断如果有一样的话就继续往后移动，如果出现有不同，先向后移动一位，再继续判断，如果还是不一样，则将第一个引用.next置为第二个引用，然后第一个引用移动过来继续往后走

链表的回文结构


public class PalindromeList {
    public boolean chkPalindrome(ListNode A) {
        ListNode cur = A; //中间节点 反转后的开端
        ListNode tmp = A;
        //找到中间节点  
        while (tmp != null && tmp.next != null) {
            tmp = tmp.next.next;
            cur = cur.next;
        }
        //反转后段链表
        tmp=cur.next;
        ListNode del=cur;
        while(tmp!=null){
             ListNode tmpNext=tmp.next;
             tmp.next=cur;
             cur=tmp;
             tmp=tmpNext;
        }
        //处理头节点
        del.next=null; 
        //判断是否为回文
       while(cur!=null){
           if(A.val!=cur.val){
               return false;
           }
           cur=cur.next;
           A=A.next;
       }
       return true;
    }
}

代码分析：

使用快慢引用先找到其中间，再将后半段链表反转，再从头部开始跟反转后的链表从头开始比较，如果有不一样的直接返回false

方法2：也可以直接将链表进行反转存入一个新的ListNode对象中，直接开始遍历比较

第二种方法比较简单~

输入两个链表，找出它们的第一个公共结点


public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        ListNode heada=headA;
        ListNode headb=headB;
        int headan=0;
        int headbn=0;
        while(heada.next!=null){
            heada=heada.next;
            headan++;
        }
        while(headb.next!=null){
            headb=headb.next;
            headbn++;
        }
        if(heada!=headb){
            return null;
        }
        heada=headA;
        headb=headB;
        if(headan>=headbn){
            while(headan-headbn>0){
                headan--;
                heada=heada.next;
            }
        } else {
                while(headbn-headan>0){
                    headbn--;
                    headb=headb.next;
                }
          }
        while(heada!=headb){
            heada=heada.next;
            headb=headb.next;
        }
        return heada;
    }
}

代码分析：

先要计算出两个链表的长度，然后进行相减找出长度长的链表，然后引用先走两个链表长度相减的差值，然后两个链表一起行动，直接相遇的第一个点即为链表的首个相交点

这个题也可以拆分成两个问题，首先是从图形中能不能看出来这是个相交的呢，我们观察可以发现如果相交的话，链表的结尾是相同的，所以我们可以让引用先走到末尾，然后看末尾是否相同，末尾相同的话就代表他们是相交的，最后是来找交点，交点还是可以使用长度的方法来做

给定一个链表，判断链表中是否有环


public class Solution {
    public boolean hasCycle(ListNode head) {
        ListNode khead=head;
        ListNode mhead=head;
        while(khead!=null&&khead.next!=null){
            khead=khead.next.next;
            mhead=mhead.next;
                if(khead==mhead){
                return true;
            }
        }
        return false;
    }
}

代码分析：

可以利用龟兔赛跑的原理，还是一个快引用一个慢引用，快引用一次走两步，慢引用一次走一步，因为链表是一个循环的，所以在任何时候，它们就算走的再远也会相遇，同样的道理，如果快引用走到了空，那么代表这个链表是没有环的

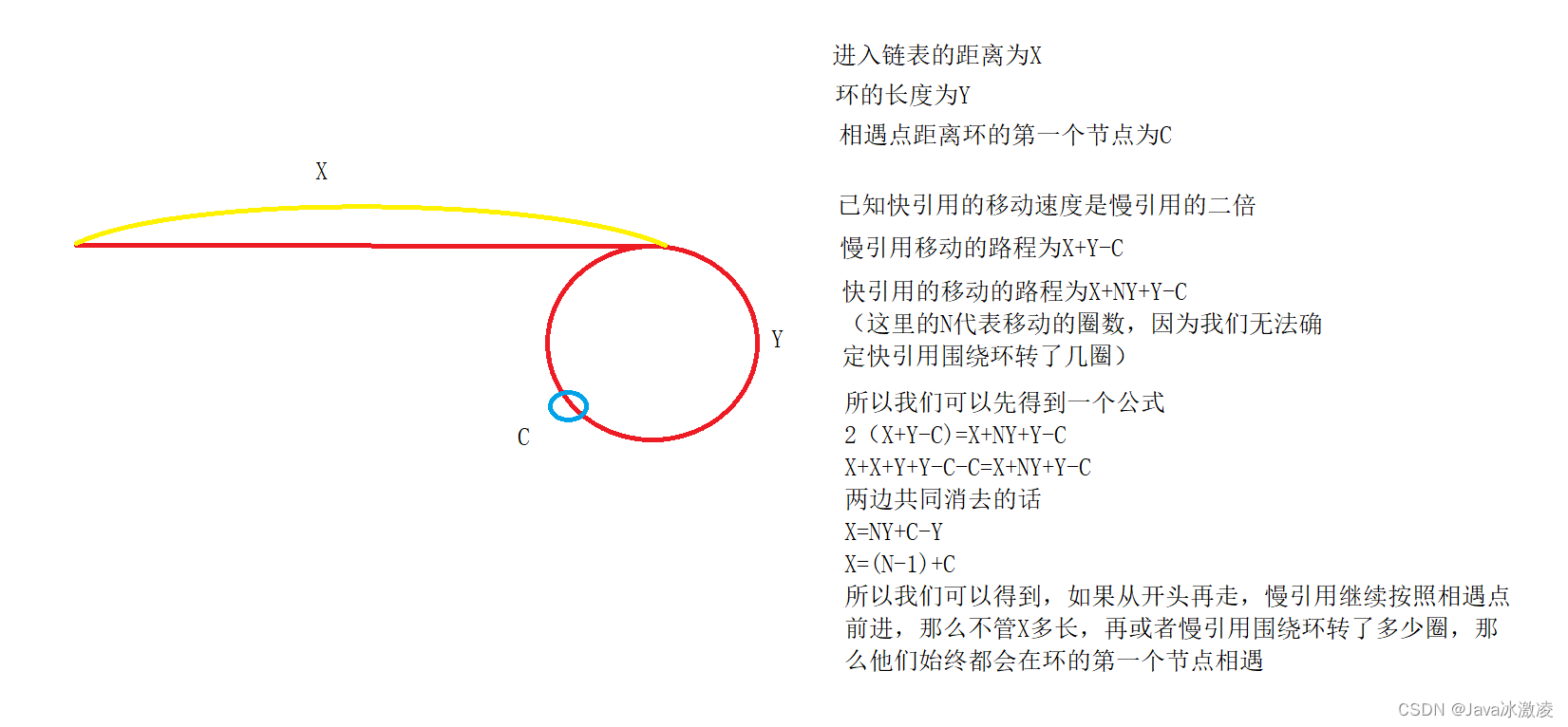
给定一个链表，返回链表开始入环的第一个节点


public class Solution {
    public ListNode detectCycle(ListNode head) {
        ListNode p=head;//慢引用
        ListNode p1=head;//快引用
        boolean pos=false;
        while(p1!=null&&p1.next!=null){
            p=p.next;
            p1=p1.next.next;
            if(p==p1){
                break;
            }
        }
        if(p1!=null&&p1.next!=null){
            pos=true;
        }
        else return null;
        //找环入口
        ListNode tmp=head;
        while(tmp!=p){
            tmp=tmp.next;
            p=p.next;
        }    
        return p;
        }
    }

代码分析：

还是需要先来判断这个链表是否有环，我们就先使用龟兔赛跑来先看是否相交，如果不相交的话那么肯定没有点可以找，则返回null

本题的证明是数学公式，慢慢领悟，想明白了很简单的

耗时5小时精心打造了此博客，希望能对您有所帮助，蟹蟹支持，如果发现博客中有错误欢迎来指出

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/Monodyee/article/detail/674213