深入浅出：探究过完备字典矩阵

在数学和信号处理的世界里，我们总是在寻找表达数据的最佳方式。在这篇博文中，我们将探讨一种特殊的矩阵——过完备字典矩阵，这是线性代数和信号处理中一个非常有趣且实用的概念。

什么是过完备字典矩阵？

首先，我们先来理解一下字典矩阵的概念。在数学上，字典矩阵基本上就是一组向量（列），它们用于表示或者重建信号或数据。如果这些列向量线性无关，我们可以将它们视为一组基，正如坐标系中的x轴和y轴一样。不过，一般的基只能刚好填满空间，每个向量只能使用一次。

但有时候，我们需要更多的向量来更加灵活地表示数据，就像适时拥有多种工具以应对不同的情况一样。这时候，过完备字典矩阵就登场了。所谓“过完备”指的是我们有更多的向量来表示空间，超出了构成空间的必需数量。

简单来说，如果我们有一个n维的空间，任何n个线性无关的向量就可以构成这个空间的一个基。然而，在过完备字典矩阵中，我们可能会有超过n个向量。这样的字典就有了冗余，但这种冗余并非没有意义。事实上，它可以允许我们有更强的表达能力，在处理信号或数据时更加灵活。

为什么需要过完备字典矩阵？

使用过完备字典矩阵有很多好处，在信号处理中尤为明显。例如，它可以增强信号去噪的能力，提供更稳健的信号表示，以及更有效的数据压缩等。

想象一下我们要将一幅图片表示为一系列的小波（一种数学函数）。一个过完备的字典允许我们用多种不同尺度和方向的小波来更好地捕捉图片中的细节，而不是仅限于一个固定基础的小波。

数值示例

假设我们在一个3维空间中，并且我们有以下3个线性无关的基向量：

import numpy as np

# 正交基
v1 = np.array([1, 0, 0])
v2 = np.array([0, 1, 0])
v3 = np.array([0, 0, 1])

# 构成正交的基矩阵
B = np.column_stack((v1, v2, v3))
print(B)
1
2
3
4
5
6
7
8
9
10

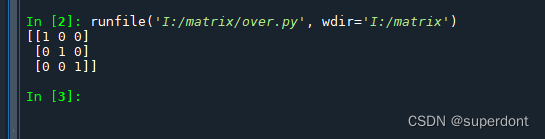
在上述情况中，我们的基矩阵B是一个3×3的单位矩阵。但在过完备的情况下，我们可能有更多的向量。让我们加上另外两个向量：

# 新增的两个向量
v4 = np.array([1, 1, 0])
v5 = np.array([1, 0, 1])

# 构成过完备字典矩阵
D = np.column_stack((v1, v2, v3, v4, v5))
print(D)
1
2
3
4
5
6
7

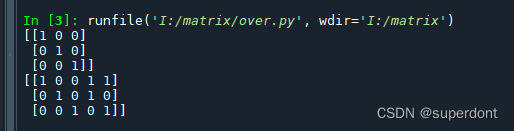
在这个例子中，矩阵D就是一个过完备字典矩阵。它有5个向量，而实际的空间维度只有3。这就意味着你可以用多种不同的线性组合来表示同一个向量或者数据点。

使用Python进行演示

为了更具体地说明过完备字典矩阵的实用性，我们可以使用Python来模拟一种实际应用场景，比如稀疏编码。

假设我们有一个信号x，我们希望用过完备字典D来表示它。实际上这涉及到一个称为稀疏表示的优化问题，我们想找到稀疏系数向量alpha，以至于D * alpha尽可能地接近信号x，同时alpha中非零元素尽可能少。

Python代码

# -*- coding: utf-8 -*-
"""
Created on Sat Feb 24 08:07:13 2024

@author: 李立宗

公众号：计算机视觉之光

知识星球：计算机视觉之光

"""

import numpy as np

# 创建一个过完备字典矩阵
# 这里，我们有一个2x3的矩阵（2维空间中的3个向量）
dictionary = np.array([[1, 0, 0.5],
                       [0, 1, 0.5]])

# 定义一个2维信号，这里我们将其转换为2x1的列向量
signal = np.array([[0.5], [0.5]])

# 我们希望找到一种表示方法，将信号表示为字典中向量的线性组合
# signal = a * dictionary[:,0] + b * dictionary[:,1] + c * dictionary[:,2]

# 使用最小二乘法来找到最佳系数（a, b, c）
coefficients, residuals, rank, s = np.linalg.lstsq(dictionary, signal, rcond=None)

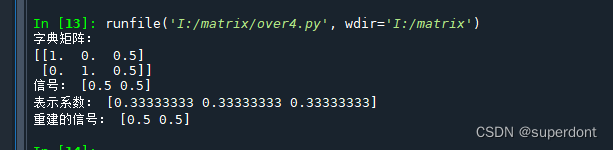
print("字典矩阵：")
print(dictionary)
print("信号：", signal.ravel())  # 使用 ravel() 将信号展平为一维数组打印
print("表示系数：", coefficients.ravel())  # 同样展平为一维数组打印

# 使用得到的系数重建信号
reconstructed_signal = dictionary @ coefficients

print("重建的信号：", reconstructed_signal.ravel())  # 展平为一维数组打印
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

输出结果

在上面的代码中我们使用了Lasso回归，它是一种用于获取稀疏解的线性模型，通过施加L1惩罚项来实现。

过完备字典矩阵的概念和应用相当广泛，它涉及线性代数、信号处理、机器学习等多个层面的知识。实际应用当中，过完备字典往往是根据特定问题设计或学习得到的，能够更好地适应该问题的需求。希望这篇简短的介绍能帮助你对过完备字典矩阵有一个直观的认识。当然，这仅仅是入门，真实的应用会更加复杂和强大。

补充资料

在Python中，对于NumPy数组，dictionary @ coefficients和dictionary.dot(coefficients)执行的操作是完全相同的。它们都是用来计算两个数组的矩阵乘法。

具体来说：

• @运算符是Python 3.5及以后版本中引入的专门用于矩阵乘法的运算符。
• .dot()方法是NumPy库提供的一个函数，用于计算两个数组的点积，对于一维数组表示向量点积，对于二维数组表示矩阵乘法。

两者的使用取决于个人偏好，但@运算符通常使代码更加简洁和易读。在实现上没有性能差异，它们背后调用的都是同样的矩阵乘法运算实现。

示例代码：

import numpy as np

A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])

# 使用 @ 运算符
result1 = A @ B

# 使用 .dot() 方法
result2 = A.dot(B)

# 结果是相同的
print("使用 @ 运算符的结果：\n", result1)
print("使用 .dot() 方法的结果：\n", result2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14

以上两种方式得到的结果都是相同的。选择哪种方式主要取决于你想要的代码风格。如果你在使用较新的Python版本，并且喜欢简洁的操作符，那么@可能是更好的选择。如果你需要在较早的Python版本（3.5之前）中保持兼容性，或者你喜欢明确表明操作的方法形式，那么.dot()可能是更适合的选择。

另一个例子

在信号处理中，过完备字典是一种允许信号以多种方式精确表示的向量集。不同于正交基的有限维度，过完备字典包含的向量个数超过了空间的维度。这样的字典能够以稀疏的方式表示原始信号，即用更少的非零系数来描述信号。

下面，我们将使用Python来展示一个简单的过完备字典的使用示例。我们会创建一个人造信号，然后构建一个过完备字典，并使用这个字典来稀疏表示该信号。

为了进行这个演示，我们将需要使用一些额外的函数库，如numpy来处理数学运算，以及matplotlib来可视化结果。同时，我们将使用scikit-learn中的OrthogonalMatchingPursuit方法来寻找信号的最佳稀疏表示。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import OrthogonalMatchingPursuit
from sklearn.decomposition import DictionaryLearning

# 设置随机数种子以获得重现性
np.random.seed(0)

# 创建一个人造的稀疏信号
n_components = 30  # 字典中原子的数目
n_features = 64  # 信号的特性数或维度
n_nonzero_coefs = 5  # 非零系数数目（稀疏性）

# 生成一个过完备字典（这个例子中我们使用随机矩阵作为字典）
dictionary = np.random.randn(n_features, n_components)

# 随机创建一个稀疏代码向量（含有非零系数的向量）
code = np.zeros(n_components)
indices = np.random.choice(range(n_components), n_nonzero_coefs, replace=False)
code[indices] = np.random.randn(n_nonzero_coefs)

# 生成信号
signal = np.dot(dictionary, code)

# 添加一些噪声
noise_level = 0.1
signal += noise_level * np.random.randn(n_features)

# 使用字典和Orthogonal Matching Pursuit算法恢复信号
omp = OrthogonalMatchingPursuit(n_nonzero_coefs=n_nonzero_coefs)
omp.fit(dictionary, signal)
coef = omp.coef_

# 恢复信号
restored_signal = np.dot(dictionary, coef)

# 可视化结果
plt.figure(figsize=(16, 6))

plt.subplot(1, 3, 1)
plt.plot(signal)
plt.title("Original signal with noise")

plt.subplot(1, 3, 2)
plt.plot(coef)
plt.title("Sparse coefficients")

plt.subplot(1, 3, 3)
plt.plot(restored_signal)
plt.title("Restored signal from dictionary")

plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

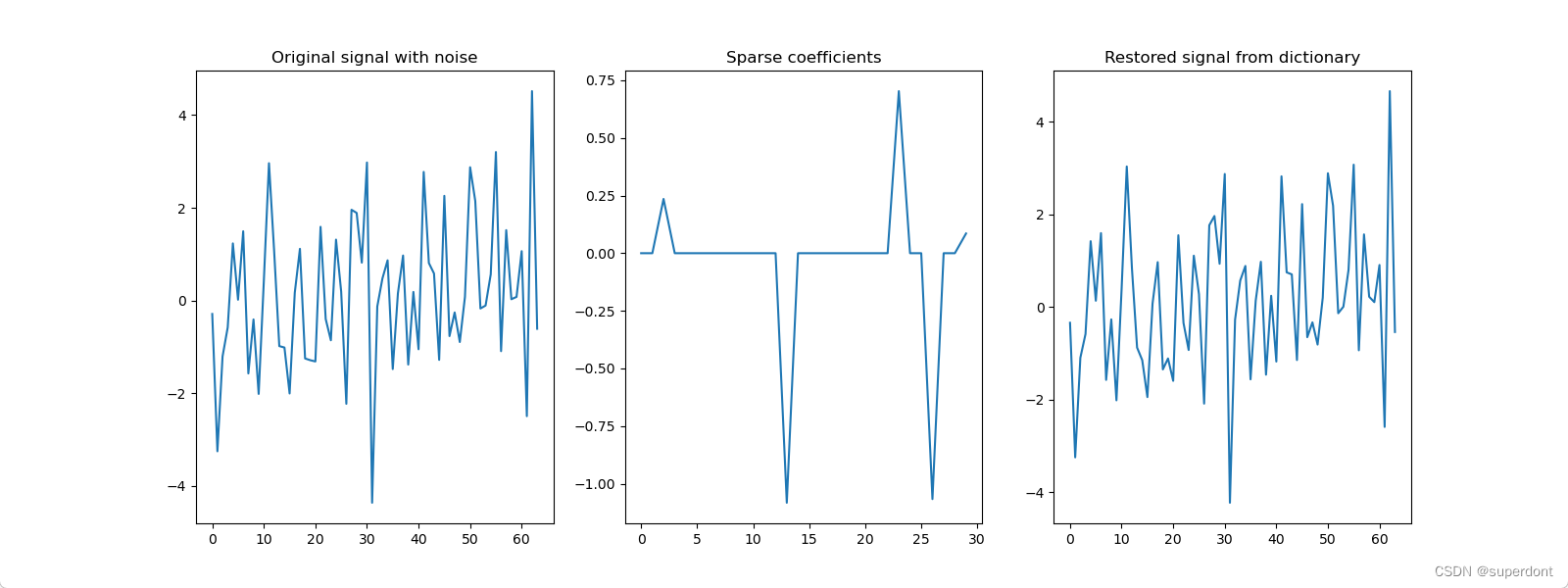
在上述代码中，我们首先创建了一个具有随机值的过完备字典。然后我们生成了一个由很少的非零系数组成的稀疏信号。接着，我们添加了一些噪声，用于模拟真实世界中的信号。使用OMP算法，我们从噪声信号中恢复了稀疏表示的系数，并且用这些系数重建了原始信号。

这个简化的演示没有包含过完备字典的创建过程，但是在实际应用中，专业的算法（如K-SVD）会被用于学习并创建用来表示特定信号集的最佳过完备字典。

总体而言，过完备字典在表示和压缩信号上具有很大的潜力，尤其是当我们想要以稀疏的方式来恢复或分析信号时。这种方法在图像和音频处理中尤其有用，例如在JPEG2000和MP3编码标准中。

相关博文

理解并实现OpenCV中的图像平滑技术

OpenCV中的边缘检测技术及实现

OpenCV识别人脸案例实战

入门OpenCV：图像阈值处理

我的图书

下面两本书欢迎大家参考学习。

OpenCV轻松入门

李立宗，OpenCV轻松入门，电子工业出版社，2023
本书基于面向 Python 的 OpenCV(OpenCV for Python)，介绍了图像处理的方方面面。本书以 OpenCV 官方文档的知识脉络为主线，并对细节进行补充和说明。书中不仅介绍了 OpenCV 函数的使用方法，还介绍了函数实现的算法原理。

在介绍 OpenCV 函数的使用方法时，提供了大量的程序示例，并以循序渐进的方式展开。首先，直观地展示函数在易于观察的小数组上的使用方法、处理过程、运行结果，方便读者更深入地理解函数的原理、使用方法、运行机制、处理结果。在此基础上，进一步介绍如何更好地使用函数处理图像。在介绍具体的算法原理时，本书尽量使用通俗易懂的语言和贴近生活的实例来说明问题，避免使用过多复杂抽象的公式。

本书适合计算机视觉领域的初学者阅读，包括在校学生、教师、专业技术人员、图像处理爱好者。
本书第1版出版后，深受广大读者朋友的喜爱，被很多高校选为教材，目前已经累计重印9次。为了更好地方便大家学习，对本书进行了修订。

计算机视觉40例

李立宗，计算机视觉40例，电子工业出版社，2022
近年来，我深耕计算机视觉领域的课程研发工作，在该领域尤其是OpenCV-Python方面积累了一点儿经验。因此，我经常会收到该领域相关知识点的咨询，内容涵盖图像处理的基础知识、OpenCV工具的使用、深度学习的具体应用等多个方面。为了更好地把所积累的知识以图文的形式分享给大家，我将该领域内的知识点进行了系统的整理，编写了本书。希望本书的内容能够对大家在计算机视觉方向的学习有所帮助。
本书以OpenCV-Python（the Python API for OpenCV）为工具，以案例为载体，系统介绍了计算机视觉从入门到深度学习的相关知识点。
本书从计算机视觉基础、经典案例、机器学习、深度学习、人脸识别应用等五个方面对计算机视觉的相关知识点做了全面、系统、深入的介绍。书中共介绍了40余个经典的计算机视觉案例，其中既有字符识别、信息加密、指纹识别、车牌识别、次品检测等计算机视觉的经典案例，也包含图像分类、目标检测、语义分割、实例分割、风格迁移、姿势识别等基于深度学习的计算机视觉案例，还包括表情识别、驾驶员疲劳监测、易容术、识别年龄和性别等针对人脸的应用案例。
在介绍具体的算法原理时，本书尽量使用通俗易懂的语言和贴近生活的示例来说明问题，避免使用复杂抽象的公式来介绍。
本书适合计算机视觉领域的初学者阅读，适于在校学生、教师、专业技术人员、图像处理爱好者使用。