代码随想录Day36 动态规划05 LeetCode T1049最后一块石头的重量II T494 目标和 T474 一和零

前言 : 动规五部曲

理论基础  : 代码随想录Day34 LeetCode T343整数拆分 T96 不同的二叉搜索树-CSDN博客

1.明白dp数组的含义

2.明白递推公式的含义

3.初始化dp数组

4.注意dp数组的遍历顺序

5.打印dp数组排错

LeetCode T1049 最后一块石头的重量II

题目链接:1049. 最后一块石头的重量 II - 力扣（LeetCode）

题目思路:

这题我们仍然采用动规五部曲来写,这题和昨天的那一道分割等和子集类似,我们先对数组求和得到sum,然后取其的一半+1作为dp数组的大小,最后我们只需要求得sum/2作为容量的背包能装的最大容量,用sum减去两倍的dp[sum/2]即可,有人问为什么这样做,我举个例子

为什么要减去两倍的dp[sum/2]呢,其实就是求两边到中间的距离的,因为是左边和右边所以减了两次

想明白了这个,我们开始使用动规五部曲来操作了

1.明白dp数组的含义

dp[j]的含义仍然是j容量的背包能装的最大价值,这里的最大价值也就是最大重量了

2.明白递推公式的含义

这里的stones的价值和重量是相等的

dp[j] = Math.max(dp[j],dp[j-stones[i]]+stones[j])

有人始终不明白这里的dp[j]后面为什么求dp[j]和dp[j-stones[i]]+stones[j]的最大值,为啥跟自己求最大值,其实这里后面的dp[j]还保存了上一层的dp[j]的大小,因为没有被更新过,所以其实不是跟自己比

3.初始化dp数组

这里因为石头的重量都是大于0的,我们全部初始化为0即可

4.注意dp数组的遍历顺序

先遍历物品,后遍历背包即可,不明白的看我的上一篇博客

代码随想录Day34 LeetCode T343整数拆分 T96 不同的二叉搜索树-CSDN博客

5.打印dp数组排错

如果遇到所求不符合了,可以去idea打印出数组来查看,这里建议使用二维数组的方式查看,更加直观

题目代码:(一维数组版本)

class Solution {
    public int lastStoneWeightII(int[] stones) {
        int sum = 0;
        for(int i: stones){
            sum+=i;
        }
        int  target = sum/2;
        int[] dp = new int[target+1];
        for(int i = 0;i<stones.length;i++){
            for(int j = target;j>=stones[i];j--){
                dp[j] = Math.max(dp[j],dp[j-stones[i]]+stones[i]);
            }
        }
        return sum-dp[target]-dp[target];
 
    }
}

题目代码:(二维数组版本)

class Solution {
    public int lastStoneWeightII(int[] stones) {
        int sum = 0;
        for(int i: stones){
            sum+=i;
        }
        int  target = sum/2;
        int[][] dp = new int[stones.length][target+1];
        for(int i = stones[0];i<=target;i++){
            dp[0][i] = stones[0];
        }
        for(int i = 1;i<stones.length;i++){
            for(int j = 1;j<=target;j++){
                //不放
                if(j<stones[i]){
                    dp[i][j] = dp[i-1][j];
                }
                //放
                else{
                    dp[i][j] = Math.max(dp[i-1][j],dp[i-1][j-stones[i]]+stones[i]);
                }
            }
        }
        return sum-dp[stones.length-1][target]*2;
 
    }
}

LeetCode T494 目标和

题目链接:494. 目标和 - 力扣（LeetCode）

题目思路:

我们也将数组按正负号划分为两个阵营,此时我们是不是只需要求一边的结果,另一边自然而然就确定了,所以这道题我们就有这样两个表达式

left//表示正的阵营
right//表示负的阵营
left + right = sum
left - right = target
left = (target+sum)/2

这里我们就知道了背包的容量为left的大小对应的表达式

这里如果我们的所求target>sum或者小于-sum都是不可能达成的

还有如果遇见target和sum的和为奇数也是不可能的,直接返回0,这是因为奇数/2是向下取整的,举个例子:

假如我的nums是[1,1,1,1,1],要求得到2

这里left明显等于3

而三个1加上两个-1得到是1,并不符合题意,实际上这个选择是无解的

接下来我们继续按照动规五部曲来走一遍

1.明白dp数组的含义

这里的dp[j]表示,容量为j的背包装满有多少种方法

2.明白递推公式的含义

dp[j] +=dp[j-nums[i]]

因为这里要求方法有多少种,举个例子

dp[5] = dp[4] + 1 其实和斐波那契数列和爬楼梯有点类似,可以相成到达5的方法数就是4的方法数+后面nums[j-nums[i]]的方法数

• 已经有一个1（nums[i]） 的话，有 dp[4]种方法 凑成 容量为5的背包。
• 已经有一个2（nums[i]） 的话，有 dp[3]种方法 凑成 容量为5的背包。
• 已经有一个3（nums[i]） 的话，有 dp[2]中方法 凑成 容量为5的背包
• 已经有一个4（nums[i]） 的话，有 dp[1]中方法 凑成 容量为5的背包
• 已经有一个5 （nums[i]）的话，有 dp[0]中方法 凑成 容量为5的背包
• 实际上求dp[5],就是把他们都累加起来

3.初始化dp数组

这里初始化dp[0] = 1,我们不要根据字面关系去理解,直接带入上面的公式理解

left = (target+sum)/2,此时left = 0,这就是一种方法

所以dp[0]要初始化为1而不是0,因为后面都得靠dp[0]推导出来,如果它为0后面的结果都是0

4.注意dp数组的遍历顺序

先遍历物品,后遍历背包

5.打印dp数组排错

题目代码:

class Solution {
    public int findTargetSumWays(int[] nums, int target) {
        int sum = 0;
        for(int i:nums){
            sum += i;
        }
        if(target>sum || target<-sum){
            return 0;
        }
        if((target + sum) % 2 == 1){
            return 0;
        }
        int bagSize = (target+sum)/2;
        int[] dp = new int[bagSize+1];
        dp[0] = 1;
        for(int i = 0;i<nums.length;i++){
            for(int j=bagSize;j>=nums[i];j--){
                dp[j] += dp[j-nums[i]];
            }
        }
        return dp[bagSize];
 
    }
}

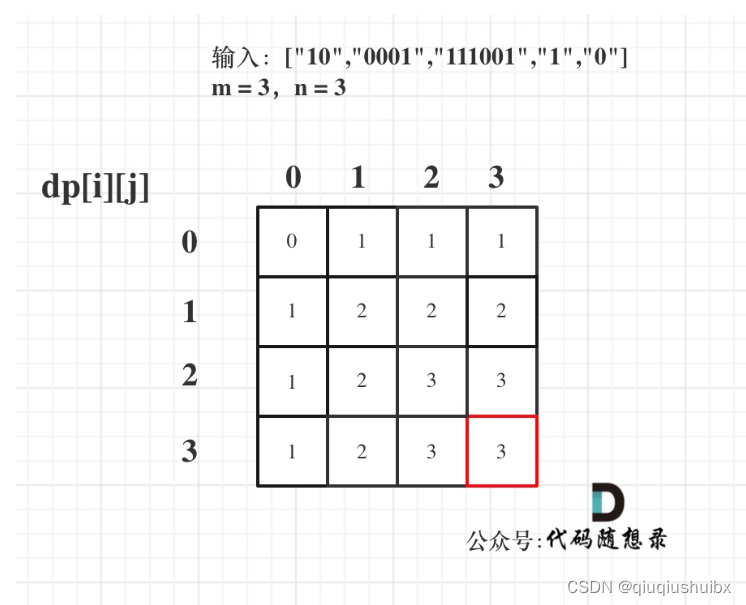
LeetCode T474 一和零

题目链接:474. 一和零 - 力扣（LeetCode）

题目思路:

这道题也是一个背包问题,虽然有点抽象,下面我们开始用动规五部曲来分析

1.明白dp数组的含义

这里的dp数组的含义就是m个0和n个1能包含的最大子集,也就是能装下m个0和n个1的背包能存放的最大物品数

2.明白递推公式的含义

我们从最初的0-1背包开始递推

dp[j] = Math.max(dp[j],dp[j - weight[i]]+value[i])

这里我们的重量其实就是i和j的个数,我们使用x代表这个物品中的'0'的个数,y代表1的个数

那么此时就转换成了

dp[i][j] = Math.max(dp[i][j],dp[i-x][j-y]+1)

因为此时如果能放进去,也就是加了1个物品

3.初始化dp数组

此时dp[0][0] 很轻易就能知道是0,为了我们的递推公式能顺利的覆盖结果,其他的也初始化为0

4.注意dp数组的遍历顺序

和之前一样,先遍历物品,再遍历背包即可

5.打印dp数组排错

题目代码:

class Solution {
    public int findMaxForm(String[] strs, int m, int n) {
        //dp数组含义
        int[][] dp = new int[m+1][n+1];
        //初始化,全为0
        for(String s:strs){
            int x = 0,y = 0;
            for(char c:s.toCharArray()){
                if(c == '0'){
                    x++;
                }else{
                    y++;
                }
            }
            for(int i = m;i>=x;i--){
                for(int j = n;j>=y;j--){
                    dp[i][j] = Math.max(dp[i][j],dp[i-x][j-y]+1);
                }
                
            }
        }
        return dp[m][n];
 
    }
}