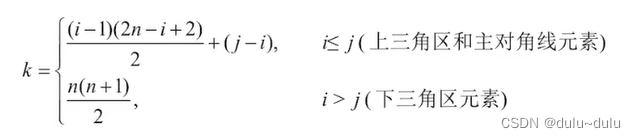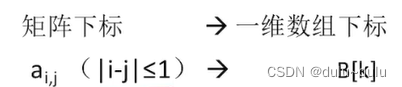weixin_40725706

这个屌丝很懒，什么也没留下！

热门标签

数据结构（五）----特殊矩阵的压缩存储

作者：weixin_40725706 | 2024-04-10 07:17:17

踩

1.一维数组的存储结构

一维数组的定义如下：

ElemType a[10];

各数组元素大小相同，且物理上连续存放。

数组元素a[i]的存放地址=LOC+i*sizeof(ElemType)。

注:除非题目特别说明，否则数组下标默认从0开始，若题目提醒下标从1开始，则存放地址为

LOC+（i-1）*sizeof(ElemType)。

2.二维数组的存储结构

二维数组定义如下：

ElemType b[2][4];

由于内存的存储空间是连续的，线性的，所以把二维数组放到内存中，有两种存放方式，行优先存放（一行一行地存）和列优先存放（一列一列地存）。

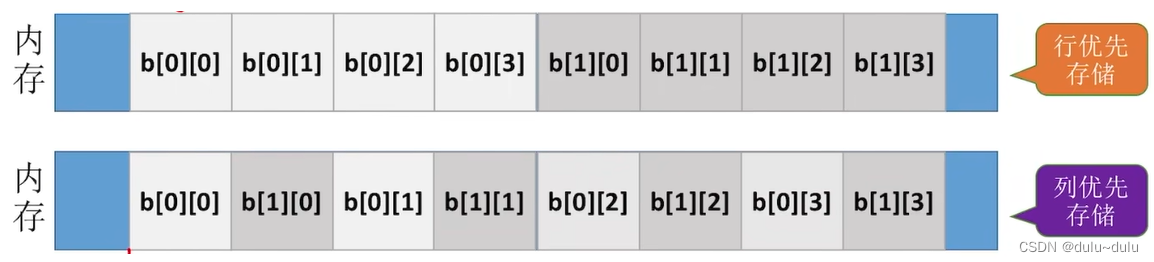
M行N列的二维数组 b[M][N]中，若按行优先存储，则

b[i][j]的存储地址 = LOC+(i*N+j)*sizeof(ElemType)

若按列优先存储，则

存储地址 = LOC+(j*M+i)*sizeof(ElemType)

3.普通矩阵的存储

普通矩阵可用二维数组存储，描述矩阵元素时，行、列号通常从1开始；而描述数组时通常下标从0开始。

4.特殊矩阵的压缩存储

（1）对称矩阵

若n阶方阵中任意一个元素 $a_{i,j}$ 都有 $a_{i,j}=a_{j,i}$ ，则该矩阵为对称矩阵。

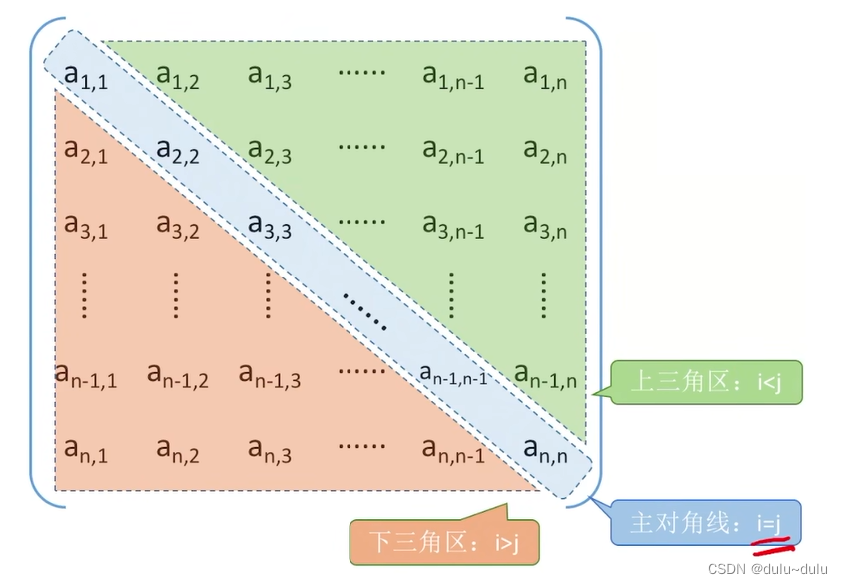
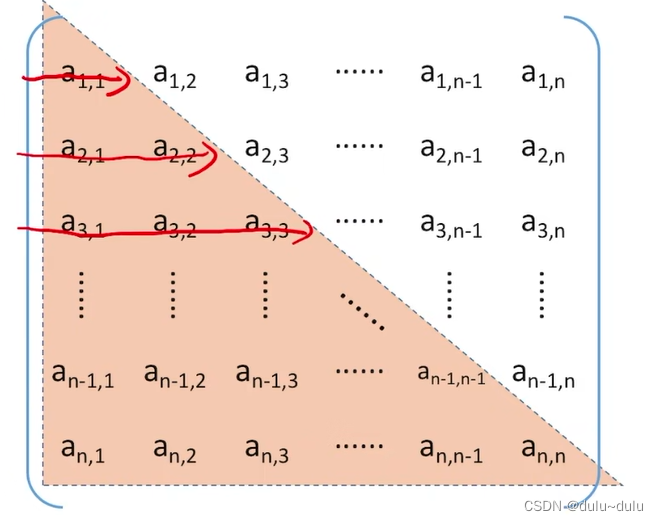
对称矩阵进行普通存储：n*n二维数组，压缩存储：只存储主对角线+下三角区。

按行优先原则将各元素存入一维数组中。

存储结构如下:

可以看到，第一行有1个元素，第二行有2个元素，第三行有3个元素，以此类推，第n行有n个元素，所以总共有1+2+3.....+n个元素，数组大小为 $\frac{(n+1)*n}{2}$

那么怎么通过矩阵下标映射到一维数组的下标呢？

例如，按行优先的原则， $a_{i,j}$ 是第几个元素？

第一行有1个元素，第二行有2个元素，以此类推，第i-1行就有i-1个元素，所以 $a_{i,j}$ 是第

$[1+2+3...+(i-1)]+j$ 个元素，即 $\frac{i(i-1)}{2}+j$ 个元素，由于数组下标是从0开始，所以

$a_{i,j}$ 的数组下标为k= $\frac{i(i-1)}{2}+j-1$ 。

若要得到上三角某个元素，那么可以根据 $a_{i,j}=a_{j,i}$ ，转换为 $a_{j,i}$ ,进而得到与下三角相同的存放规律。

进而其一维数组下标为：

$\frac{j(j-1)}{2}+i-1$

总结：

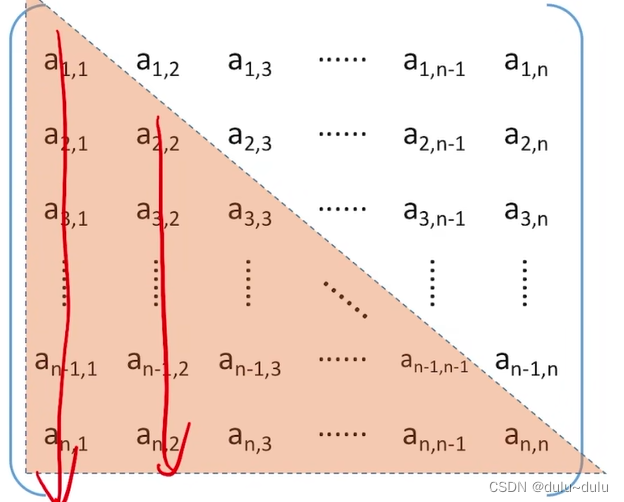
按照列优先原则进行存储， $a_{i,j}$ 是第几个元素？

如上图所示，第1列有n个元素，第2列有n-1个元素，第j-1列有n-j+2个元素。

技巧：1+n=n+1，2+(n-1)=n+1,(n-1)+(n-j+2)=n+1

第j列有多少元素，用（行号 - 列号+1）即可，可以自己验算一下。

所以 $a_{i,j}$ 是第

$[n+(n-1)+(n-2)....+(n-j+2)]+(i-j)+1$ 个元素

默认从0开始的话，数组下标在上面的基础上减1即可： $[n+(n-1)+(n-2)....+(n-j+2)]+(i-j)$

由等差数列易得：

$S_{n}=\frac{n(a1+an)}{2}=\frac{(j-1)(2n-j+2)}{2}$

所以 $a_{i,j}$ 的下标为：

$\frac{(j-1)(2n-j+2)}{2}+(i-j)$

（2）三角矩阵

下三角矩阵：除了主对角线和下三角区，其余的元素都相同。

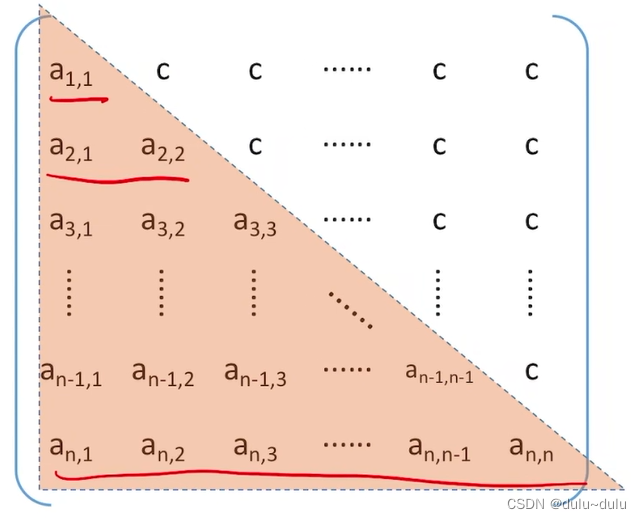
压缩存储：按行优先原则将橙色区元素存入一维数组中。并在最后一个位置存储常量c。

所以一维数组的长度：(1+2+3.....n)+1

若按照行优先的原则， $a_{i,j}$ 是第几个元素：

下三角和对称矩阵的运算一样，对于上三角，由于上三角每个元素都是一样的，所以映射到一维数组的最后一个元素，即B[ $\frac{n*(n+1)}{2}$ ]

上三角矩阵：除了主对角线和上三角区，其余的元素都相同。

按照行优先原则， $a_{i,j}$ 是第几个元素？

第1行到第i-1行有 $[n+(n-1)+.....+(n-i+2)]$

第i行有j-i+1个元素：列号(j)-行号(i)得到该元素在第i行的前面有多少元素。

所以 $a_{i,j}$ 是第

$[n+(n-1)+.....+(n-i+2)]+(j-i)+1$ 个元素。

其数组下标为：

$[n+(n-1)+.....+(n-i+2)]+(j-i)$

由等差数列的求和公式易得：

$S_{n}=[n+(n-1)+.....+(n-i+2)]=\frac{n(a1+an)}{2}=\frac{(i-1)(2n-i+2)}{2}$

要访问下三角区的话同理，直接映射到一维数组的最后一个位置。

总结:

（3）三对角矩阵

三对角矩阵，又称带状矩阵：当|i-j|>1时，有 $a_{i,j}$ =0(1≤i，j≤n)，通俗点来讲就是，主对角线元素及其上下左右的元素不为0，其余元素的值全为0。

压缩存储：按行优先(或列优先)原则，只存储带状部分。

可以观察到，带状矩阵除了第一行和最后一行是两个元素，其余行都是三个元素。所以要存储的元素个数为：3*n-2

若默认数组下标从0开始，那么最后一个元素的数组下标就为：B[3n-3]

那么按行优先的原则， $a_{i,j}$ 是第几个元素?

前 i-1 行共 3(i-1)-1 个元素。

$a_{i,j}$ 是第i行的 j-i+2 个元素。

那么将两个数加起来： $a_{i,j}$ 是第 2i+j-2个元素

为什么有j-i+2呢？

由上三角矩阵我们可以分析得， $a_{i,j}$ 的元素在第i行的前面有j-i个元素，例如 $a_{1,2}$ ,前面就有：

2-1=1个元素。

对比这里，把三角形往前挪一个位置，可以得到相同的在第i行的前面的元素的个数，所以 $a_{i,j}$ 在第i行，前面有j-i+1个元素，那么加上它本身 $a_{i,j}$ 是第i行第j-i+2个元素。

我是这么理解的，不管怎么理解，只要自己理解就可以啦~

有些人也会有疑问， $a_{i,j}$ 是第i行的 j-i+2 个元素针对第一行就不对呀？其实结合前 i-1 行共 3(i-1)-1 个元素，针对第一行计算得到-1，再加上j-i+2 也是对的结果。

例如： $a_{1,2}$

根据式子3(i-1)-1，前i-1(0)行有-1个元素，再根据式子： $a_{i,j}$ 是第i行的 j-i+2 个元素，得到

2-1+2=3个元素，那么最后两者相加3+(-1)=2，得到的也是正确的结果，也就是 $a_{1,2}$ 是第2个元素。

那么第k+1个元素，在第几行?第几列?

前 i-1 行共 3(i-1)-1个元素

前 i 行共 3 i-1 个元素

显然，3(i-1)-1< k+1 ≤ 3i-1

不等式解出来为： $i\geq (k+2)/3$ ，且 $i<(k+5)/3$

因为i是行号，一定是正整数，将这个式子向上取整，即 i= $\left \lceil i\geq (k+2)/3\right \rceil$ ，就可以满足i"刚好"大于等于某一行。

王道书中的逻辑：第k+1个元素前有k个元素，并且k满足3(i-1)-1 ≤ k ＜ 3i-1

不等式解出来为： $i \leq (k+2)/3+1$ ，且 $i>(k+1)/3$

将这个式子向下取整，即 i= $\left \lfloor i \leq (k+2)/3+1 \right \rfloor$ ，即可满足i“刚好”小于等于某一行。

由于我们之前讲到过 $a_{i,j}$ 是第 2i+j-2个元素，其下标默认从0开始，就是2i+j-3，所以：k=2i+j-3，所以我们就可以从 k 和 i 推出j的值了。

（4）稀疏矩阵的压缩存储

稀疏矩阵就是非零元素远远少于矩阵元素的个数。

压缩存储：

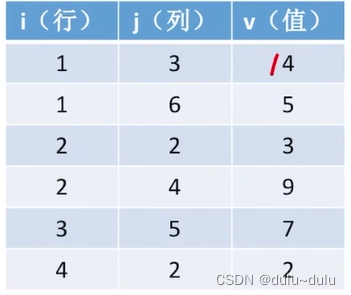
1.顺序存储---三元组<行，列，值>，这里存储的值都是稀疏矩阵中的非0元素。

注：此处行、列标从1开始

若用这种方式存储稀疏矩阵，想要访问其中的某个元素，只能顺序依次扫描三元组，会失去随机存取的特性。

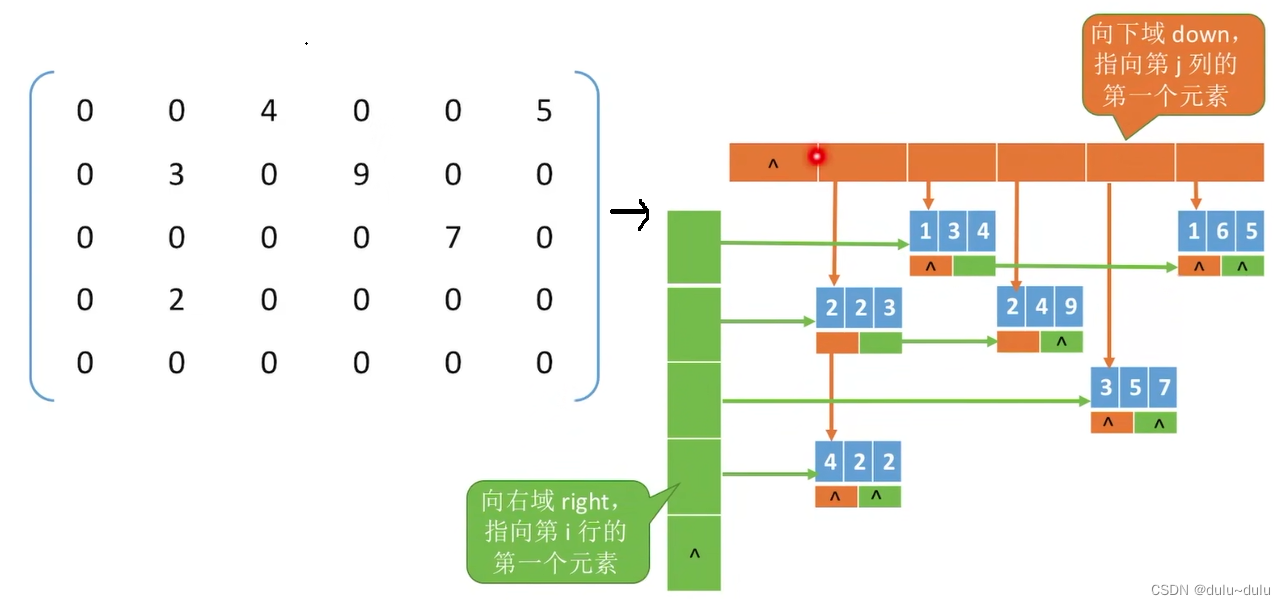
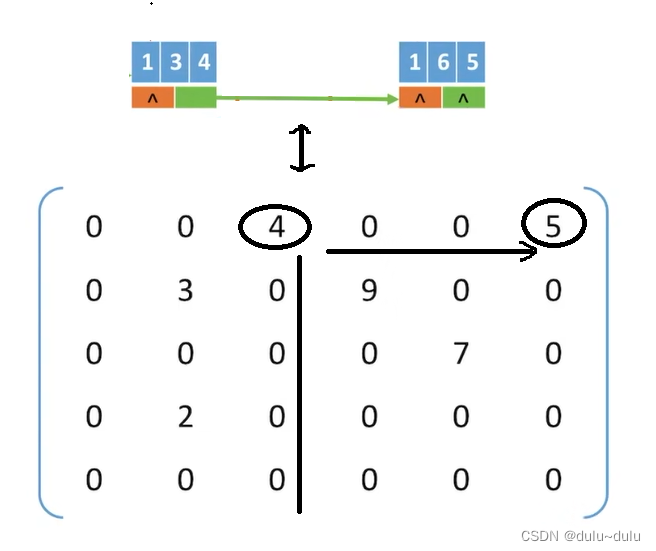
2.链式存储---十字链表法。如图所示，向下域down指向第j列的第一个元素，向右域 right,指向第i行的第一个元素。

每个非0元素会对应一个结点，这个结点包括该非0元素所在的行，列以及对应的值；还会包含两个指针，第一个指针指向同列的下一个元素，第二个指针指向同行的下一个元素。可以看图自己分析一下。

例如：该结点第一个指针为空，表示该列没有非0元素了；第二个结点指向了同行的下一个元素，即5。

以上公式不建议死记硬背，充分理解之后，考场上也可以推出来的。

公式是没有错的，附上了自己的理解，如果哪个公式不懂可以评论区或私信我，如果哪里理解错误，可以评论区纠正，若有更好的方法，可以在评论区分享出来！谢谢佬们

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/weixin_40725706/article/detail/397300