- 1微众银行李辉忠:数据安全问题变迁,呼唤隐私计算入场
- 2完美解决:“已损坏,无法打开。 您应该将它移到废纸篓。”_已损坏,无法打开。 你应该将它移到废纸篓。
- 3Ipone桌面计算机没了,苹果笔记本桌面图标不见了怎么办
- 4【机器学习算法】奇异值分解(SVD)_svd奇异值分解
- 5vue+axios请求时设置请求头(带上token)_vue设置公共请求头
- 6python实验四_20191318实验四 《Python程序设计》实验报告
- 710个Python爬虫入门实例,建议收藏!!_python爬虫简单例子
- 8Flask基础2-Jinja2模板
- 9【2024最新华为OD-C/D卷试题汇总】[支持在线评测] 虚拟理财游戏(100分) - 三语言AC题解(Python/Java/Cpp)
- 10单目深度估计方法综述及编程实现_单目相机怎么得到深度信息
排序算法进阶——归并排序【详细图解,递归和非递归】_归并排序的递归执行示意图
赞
踩
归并算法
在了解归并排序之前让我们先了解一下归并这一算法吧!
归并算法一般应用于合并两个已经有序的序列,使合并后的序列也有序,是一个时间复杂度为O(N)的算法,不过一般要借助两个要排序的序列的元素个数个额外的空间。
一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一
基本思想:
既然要排序的两个序列已经有序,那么就可以先申请两个序列元素之和大小的空间,再比较两个序列的第一个元素的大小,将小的那一个元素放在申请的空间的第一个【假设排升序】,再让放入的那个元素之后的一个元素与那个第一次比较时没放入的元素比较,再把小的那一个放入申请空间的第二个位置上…
直到有有一个序列已经全部放入了申请的空间,此时另一序列的剩下的元素都大于放完序列的最大值,所以可以直接将它剩下的元素全部放入申请空间。
如下图

一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一
具体代码实现:
定义两个指针指向两个序列的第一个元素,如果左侧序列的指针指向的元素更小就把它放入申请的空间,否则将右侧序列的元素放入申请空间
借此构成一个循环,循环结束条件是两个指针中有一个指向序列的最后一个元素之后就结束

一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一
归并排序
基本思想
有了归并算法后,我们知道只要要排序的两个序列是有序的我们就可以轻松地排出一个有序序列
同理如果将一个序列分成两半,如果它坐边有序右边也有序,就可以直接用归并算法整个序列有序。
那么怎么让左右两边的序列有序呢?
我们知道如果序列中只有一个序列时那它肯定是有许的,既然如此,
我们让要排序列的左侧序列和右侧的元素个数为1
此时,不就左右有序可以归并了吗。
如何完成这个操作呢?
有两个方法
一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一
方法一:递归
将序列分成两半在,分成的两半再分别分成两半…。直到左序列和右序列的元素个数都为1时再从小区间归并到大区间
如下图
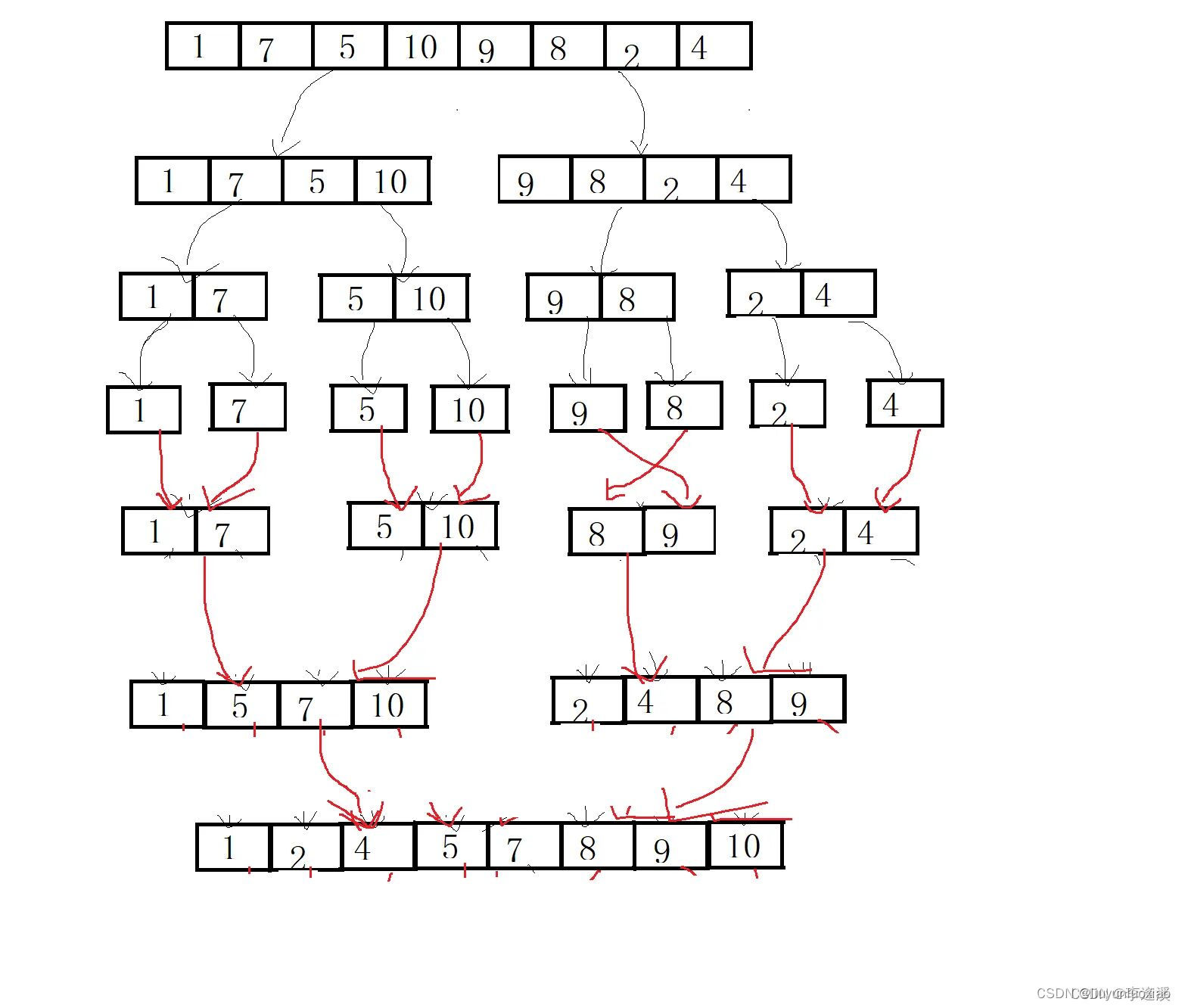
该过程可用递归实现。
一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一
实现方法:
先申请于序列等大的空间,再创建用于递归的函数

再实现递归函数
先将左右区间递归到都只有一个元素

浅浅画了一下递归展开图


left=2,right=3时也类似
做完以上的递归之后,左右区间的元素个数就都只有1了(如上图的左区间【0-0】,右区间【1~1】),此时从大区间向小区间的递归就结束了
然后开始向下执行代码,进行归并,
小区间时的代码执行完后,会自动返回到调用这一小区间的位置,即更大的区间的函数中,继续向下执行代码


具体过程可参考下图【注意:left和right是下标】


一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一
完整代码:
void D_MereSort(int a[], int left, int right, int* tmp) { //left和right分别为递归区间的左右端点的下标 //把要归并的两边的区间递归到各只有1个元素就停 if (left >= right) return; //mid为递归区间中间下标 int mid = (left + right) / 2; //递归 D_MereSort(a, left, mid, tmp); D_MereSort(a, mid+1, right, tmp); //定义begin和end接受left和right //防止left和right改变,导致出错 int begin1 = left, end1 = mid; int begin2 = mid+1, end2 = right; //i必须有且值只能是 左侧区间的左端点 即left int i = left; //归并算法 while (begin1 <= end1 && begin2 <=end2) { if (a[begin1] < a[begin2]) { tmp[i++] = a[begin1++]; } else { tmp[i++] = a[begin2++]; } } while (begin1 <= end1) { tmp[i++] = a[begin1++]; } while (begin2 <= end2) { tmp[i++] = a[begin2++]; } int j = left; //将归并好的放回要排序的数组 for (; j<=right; j++) a[j] = tmp[j]; } //归并排序(递归) void MergeSort1(int a[], int n) { //创建临时空间,方便归并 int* tmp = (int*)malloc(sizeof(int) * n); //用于递归的函数 D_MereSort(a, 0, n - 1, tmp); //释放申请空间 free(tmp); }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一
方法二:利用下标变化直接在数组中归并【非递归】
如下图

实现方法:
设gap为左右区间的元素个数
j为循环变化的下标,这样可以将
归并的区间划分为
【i,i+gap-1】【i+gap,i+2*gap-1】

将区间划分为【i,i+gap-1】【i+gap,i+2*gap-1】
可能会出现越界的情况
- 其中i+gap-1越界和i+gap越界的处理方法相同
- i+2*gap-1
如下图



一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一
完整代码:
void MergeSort2(int a[], int n) { //申请空间 int* tmp = (int*)malloc(sizeof(int) * n); //gap表示归并的左右区间的元素个数 int gap = 1; int j = 0; while (gap < n)//gap不能等于数组的总元素个数 { for (j = 0; j < n; j += 2 * gap) { int i = j; //防止循环变量改变,影响循环 int begin1 = i, end1 = i + gap - 1; int begin2 = i + gap, end2 = i + 2 * gap - 1; if (begin2 >= n)//右区间 左端点越界,就直接可以结束 break; if (end2 >= n)//右区间 右端点越界,就将它改为n-1 end2 = n - 1; //归并 while (begin1 <= end1 && begin2 <= end2) { if (a[begin1] < a[begin2]) { tmp[i++] = a[begin1++]; } else { tmp[i++] = a[begin2++]; } } while (begin1 <= end1) { tmp[i++] = a[begin1++]; } while (begin2 <= end2) { tmp[i++] = a[begin2++]; } } int z = 0; //归并结束后,将归并完成的拷贝回去 //为下次循环的归并做准备 for (z = 0; z < n; z++) a[z] = tmp[z]; gap *= 2; } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一
归并排序的时间复杂度
归并排序的递归版本是将区间从大向小分,一次一半
我们可以将该过程类似二叉树

我们把每一层归并操作消耗的时间记作n。
现在,我们只需要知道这棵树的高度h,用高度h乘以每一层的时间消耗n,就可以得到总的时间复杂度O(n∗h)。从归并排序的原理和递归树,可以看出来,归并排序递归树是一棵满二叉树。
而满二叉树的高度大约是log2n
所以,归并排序递归实现的时间复杂度就是O(nlogn)。
一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一
归并排序的空间复杂度
归并排序需要借助与数组等大的区间
所以
归并排序的空间复杂度为O(N)
一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一
归并排序的稳定性
归并排序采用分治策略,将序列递归地分成短序列,然后将各个有序的短序列合并成一个有序的长序列,不断合并直到原序列全部排好序。
在合并过程中,如果两个当前元素相等时,归并排序会把处在前面的序列的元素保存在结果序列的前面,从而保证了稳定性。
所以归并排序是稳定的
一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一
以上就是全部内容了,如果对你有帮助的话,可以点赞支持一下!!!



