PyTorch: nn网络层-卷积层_pytorch卷积层

文章和代码已经归档至【Github仓库：https://github.com/timerring/dive-into-AI 】或者公众号【AIShareLab】回复 pytorch教程 也可获取。

nn网络层-卷积层

1D/2D/3D 卷积

卷积有一维卷积、二维卷积、三维卷积。一般情况下，卷积核在几个维度上滑动，就是几维卷积。比如在图片上的卷积就是二维卷积。

一维卷积

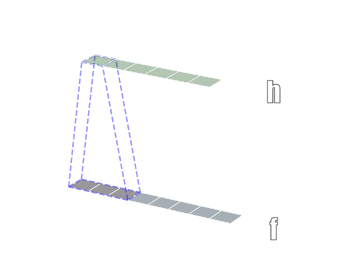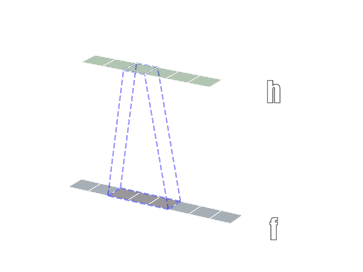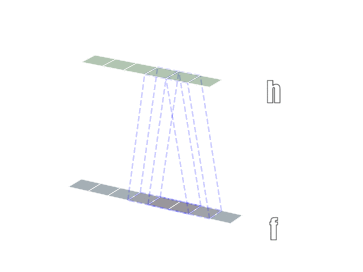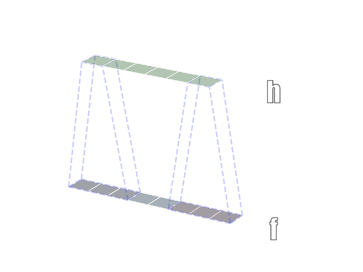
二维卷积

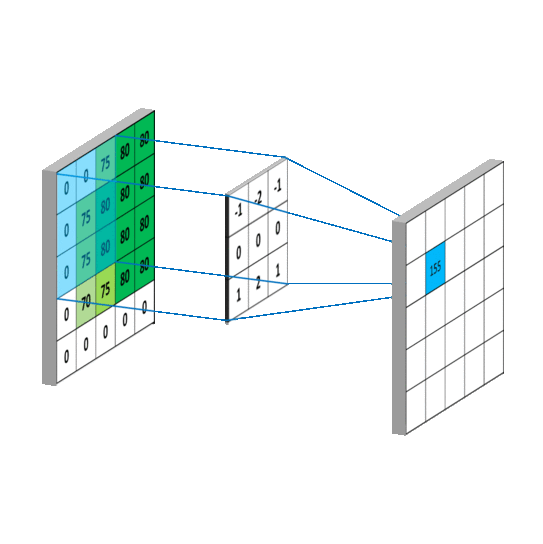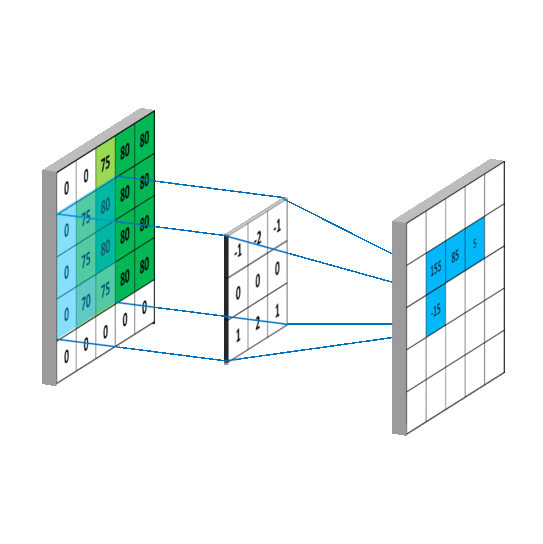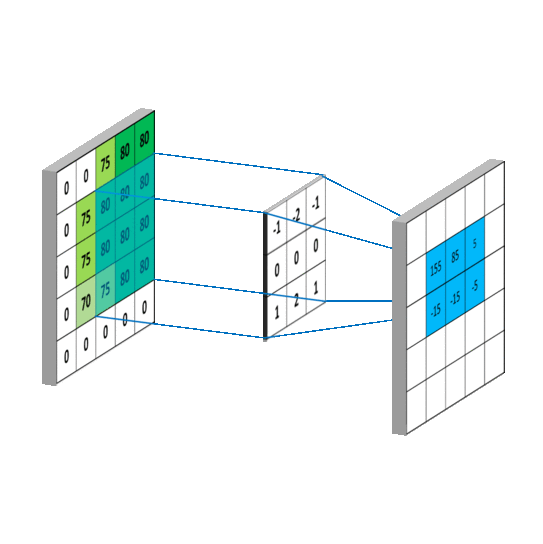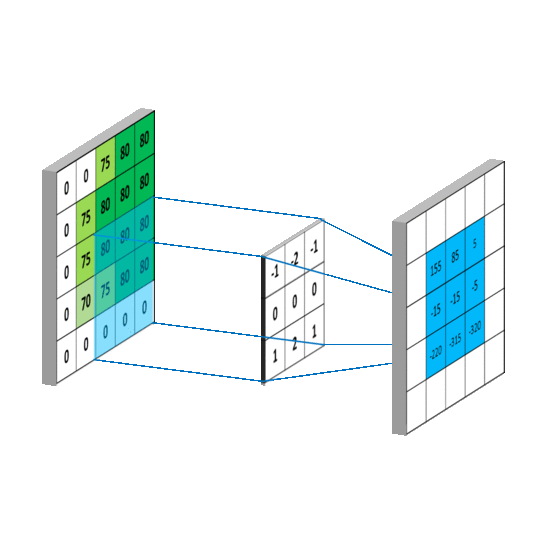
三维卷积

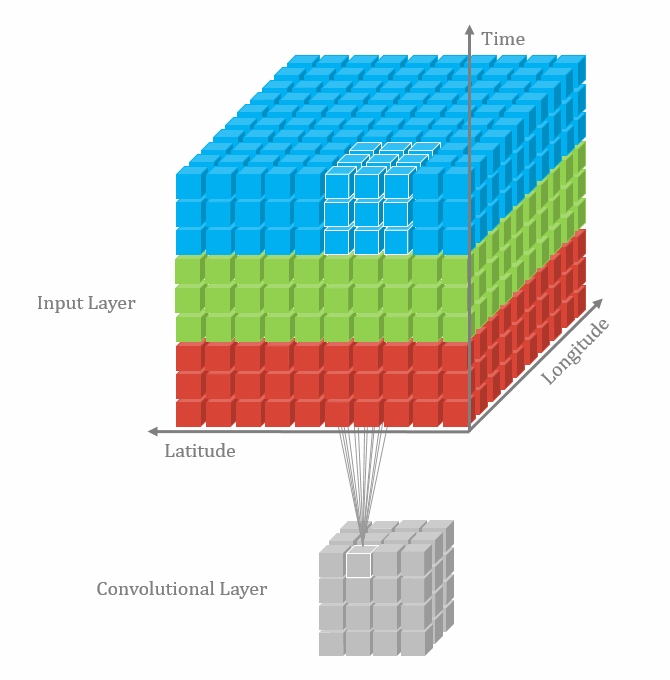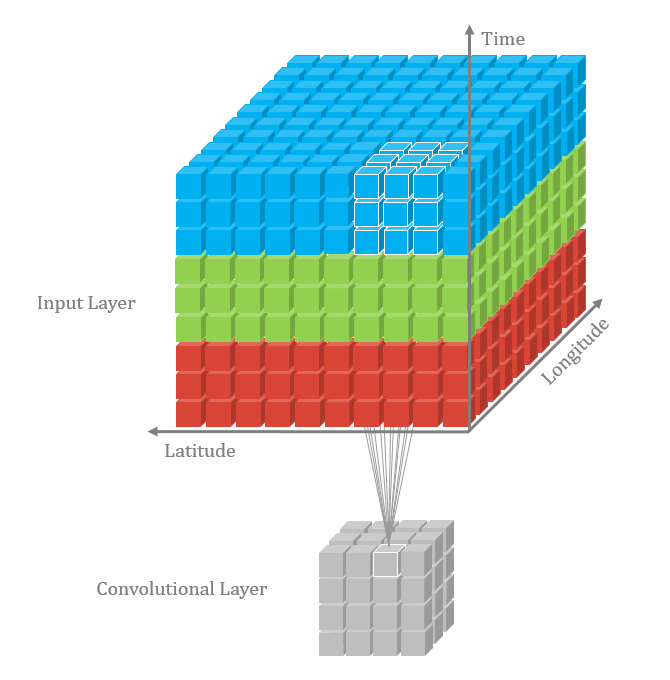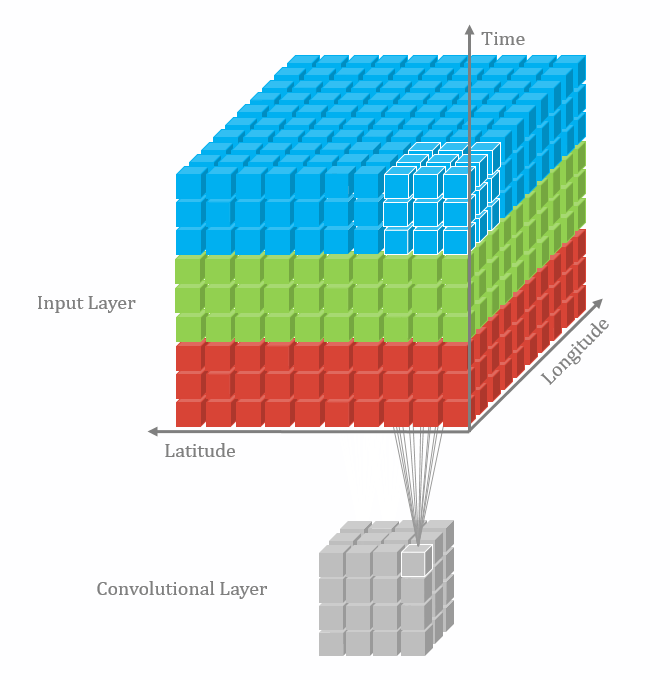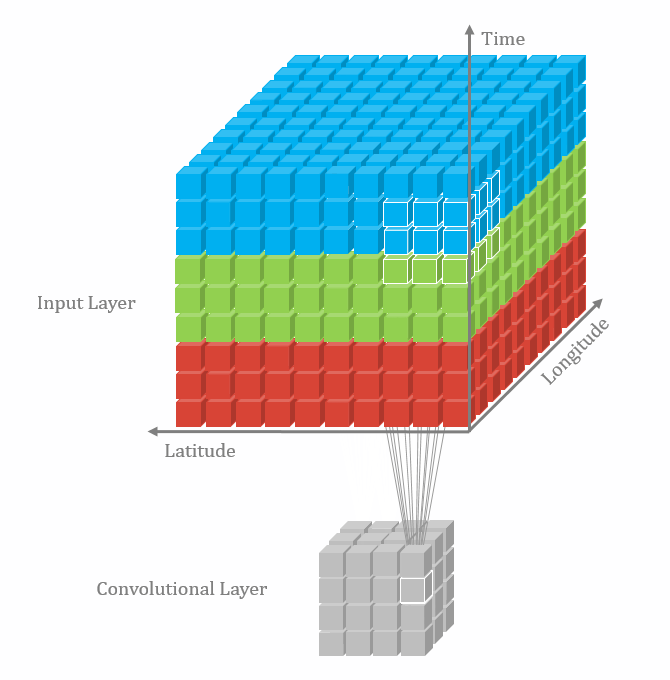
二维卷积：nn.Conv2d()

nn.Conv2d(self, in_channels, out_channels, kernel_size, stride=1,
                 padding=0, dilation=1, groups=1,
                 bias=True, padding_mode='zeros')
1
2
3

这个函数的功能是对多个二维信号进行二维卷积，主要参数如下：

• in_channels：输入通道数
• out_channels：输出通道数，等价于卷积核个数
• kernel_size：卷积核尺寸
• stride：步长
• padding：填充宽度，主要是为了调整输出的特征图大小，一般把 padding 设置合适的值后，保持输入和输出的图像尺寸不变。
• dilation：空洞卷积大小，默认为 1，这时是标准卷积，常用于图像分割任务中，主要是为了提升感受野
• groups：分组卷积设置，主要是为了模型的轻量化，如在 ShuffleNet、MobileNet、SqueezeNet 中用到
• bias：偏置

卷积尺寸计算

简化版卷积尺寸计算

这里不考虑空洞卷积，假设输入图片大小为 $ I \times I$，卷积核大小为 $k\times k$，stride 为 $s$，padding 的像素数为 $p$，图片经过卷积之后的尺寸 $ O $ 如下：

$O=\frac{I-k+2\times p}{s}+1$

下面例子的输入图片大小为 $5\times 5$，卷积大小为 $3\times 3$，stride 为 1，padding 为 0，所以输出图片大小为 $\frac{5-3+2\times 0}{1}+1=3$。

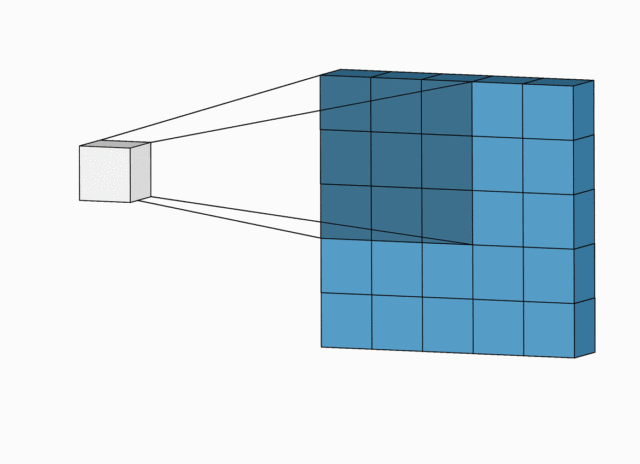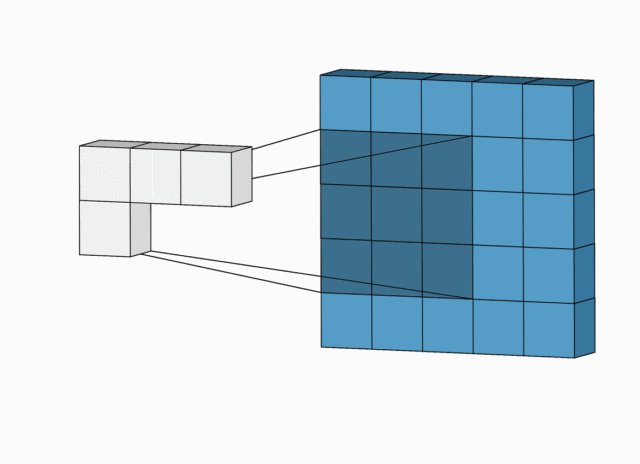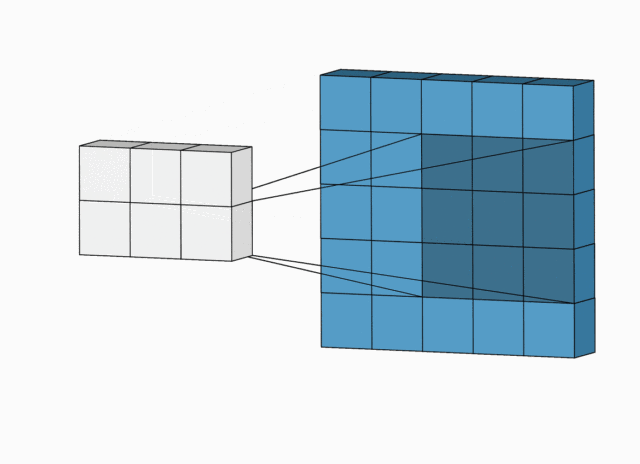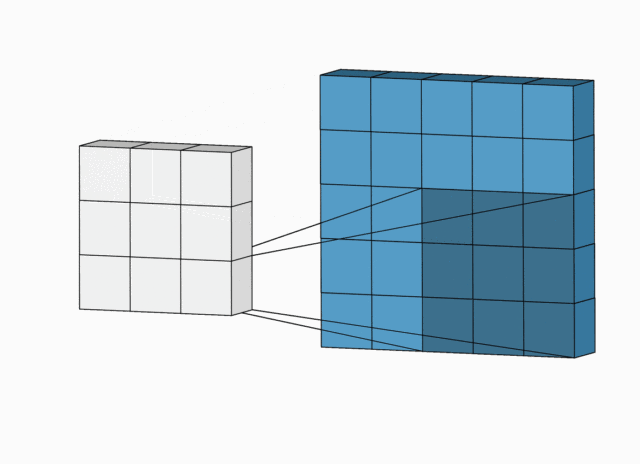
完整版卷积尺寸计算

完整版卷积尺寸计算考虑了空洞卷积，假设输入图片大小为 $ I \times I$，卷积核大小为 $k\times k$，stride 为 $s$，padding 的像素数为 $p$，dilation 为 $d$，图片经过卷积之后的尺寸 $ O $ 如下：。

$O=\frac{I-d\times (k-1)+2\times p-1}{s}+1$

卷积网络示例

这里使用 input * channel 为 3，output_channel 为 1 ，卷积核大小为 $3\times 3$ 的卷积核nn.Conv2d(3, 1, 3)，使用nn.init.xavier_normal*()方法初始化网络的权值。代码如下：

import os
import torch.nn as nn
from PIL import Image
from torchvision import transforms
from matplotlib import pyplot as plt
from common_tools import transform_invert, set_seed

set_seed(3)  # 设置随机种子

# ================================= load img ==================================
path_img = os.path.join(os.path.dirname(os.path.abspath(__file__)), "imgs", "lena.png")
print(path_img)
img = Image.open(path_img).convert('RGB')  # 0~255

# convert to tensor
img_transform = transforms.Compose([transforms.ToTensor()])
img_tensor = img_transform(img)
# 添加 batch 维度
img_tensor.unsqueeze_(dim=0)    # C*H*W to B*C*H*W

# ================================= create convolution layer ==================================

# ================ 2d
flag = 1
# flag = 0
if flag:
    conv_layer = nn.Conv2d(3, 1, 3)   # input:(i, o, size) weights:(o, i , h, w)
    # 初始化卷积层权值
    nn.init.xavier_normal_(conv_layer.weight.data)
	# nn.init.xavier_uniform_(conv_layer.weight.data)
    # calculation
    img_conv = conv_layer(img_tensor)

# ================ transposed
# flag = 1
flag = 0
if flag:
    conv_layer = nn.ConvTranspose2d(3, 1, 3, stride=2)   # input:(input_channel, output_channel, size)
    # 初始化网络层的权值
    nn.init.xavier_normal_(conv_layer.weight.data)

    # calculation
    img_conv = conv_layer(img_tensor)

# ================================= visualization ==================================
print("卷积前尺寸:{}\n卷积后尺寸:{}".format(img_tensor.shape, img_conv.shape))
img_conv = transform_invert(img_conv[0, 0:1, ...], img_transform)
img_raw = transform_invert(img_tensor.squeeze(), img_transform)
plt.subplot(122).imshow(img_conv, cmap='gray')
plt.subplot(121).imshow(img_raw)
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

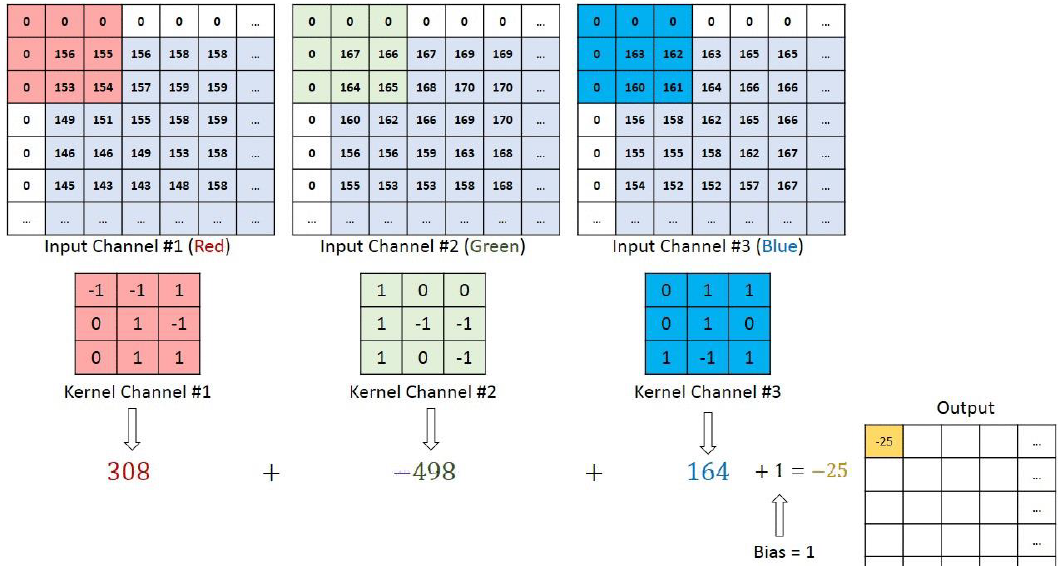
通过conv_layer.weight.shape查看卷积核的 shape 是(1, 3, 3, 3)，对应是(output_channel, input_channel, kernel_size, kernel_size)。所以第一个维度对应的是卷积核的个数，每个卷积核都是(3,3,3)。虽然每个卷积核都是 3 维的，执行的却是 2 维卷积。下面这个图展示了这个过程。

也就是每个卷积核在 input_channel 维度再划分，这里 input_channel 为 3，那么这时每个卷积核的 shape 是(3, 3)。3 个卷积核在输入图像的每个 channel 上卷积后得到 3 个数，把这 3 个数相加，再加上 bias，得到最后的一个输出。

转置卷积：nn.ConvTranspose()

转置卷积又称为反卷积 (Deconvolution) 和部分跨越卷积 (Fractionally strided Convolution)，用于对图像进行上采样。

正常卷积如下：

原始的图片尺寸为 $4\times 4$，卷积核大小为 $3\times 3$，$padding=0$，$stride=1$。由于卷积操作可以通过矩阵运算来解决，因此原始图片可以看作 $16\times 1$ 的矩阵 $I_{16\times 1}$，

为什么是16 * 1，因为16是它所有的像素点个数，1是它的图片张数。

卷积核可以看作 $4\times 16$ 的矩阵 $K_{4\times 16}$，其中，那么输出是 $K_{4\times 16}\times I_{16\times 1}=O_{4\times 1}$ 。（是卷积核 * 图像）

这里的4是输出特征图像素值的总个数，16是通过卷积核补零，符合原图片像素点个数得到的。

转置卷积如下：

原始的图片尺寸为 $2\times 2$，卷积核大小为 $3\times 3$，$padding=0$，$stride=1$。由于卷积操作可以通过矩阵运算来解决，因此原始图片可以看作 $4\times 1$ 的矩阵 $I_{4\times 1}$，

这里的4同样是原图的像素点个数。

卷积核可以看作 $4\times 16$ 的矩阵 $K_{16\times 4}$，

这里的4不再是通过补零得到的，而是通过剔除得到的。如上图，本来卷积核有9个像素点，但是在实际的情况中卷积核最大只能计算到4个像素点，因此这里就是4。

16是根据输入公式计算得到的输出图片的大小。

那么输出是 $K_{16\times 4}\times I_{4\times 1}=O_{16\times 1}$ 。

正常卷积核转置卷积矩阵的形状刚好是转置关系，因此称为转置卷积，但里面的权值不是一样的，卷积操作也是不可逆的，简单来讲，就是一张图片经过卷积，然后再经过转置卷积，无法得到原来的图片。

PyTorch 中的转置卷积函数如下：

nn.ConvTranspose2d(self, in_channels, out_channels, kernel_size, stride=1,
                 padding=0, output_padding=0, groups=1, bias=True,
                 dilation=1, padding_mode='zeros')
1
2
3

和普通卷积的参数基本相同。

转置卷积尺寸计算

简化版转置卷积尺寸计算

这里不考虑空洞卷积，假设输入图片大小为 $ I \times I$，卷积核大小为 $k\times k$，stride 为 $s$，padding 的像素数为 $p$，图片经过卷积之后的尺寸 $ O $ 如下，刚好和普通卷积的计算是相反的：

$O=(I-1)\times s+k$

${\text{ out }}_{\text{size }}=\left({\text{ in }}_{\text{size }}-1\right)\ast stride+{\text{ kernel }}_{\text{size }}$

完整版简化版转置卷积尺寸计算

$O=(I-1)\times s-2\times p+d\times (k-1)+ou{t}_{p}adding+1$

转置卷积代码示例如下：

import os
import torch.nn as nn
from PIL import Image
from torchvision import transforms
from matplotlib import pyplot as plt
from common_tools import transform_invert, set_seed

set_seed(3)  # 设置随机种子

# ================================= load img ==================================
path_img = os.path.join(os.path.dirname(os.path.abspath(__file__)), "imgs", "lena.png")
print(path_img)
img = Image.open(path_img).convert('RGB')  # 0~255

# convert to tensor
img_transform = transforms.Compose([transforms.ToTensor()])
img_tensor = img_transform(img)
# 添加 batch 维度
img_tensor.unsqueeze_(dim=0)    # C*H*W to B*C*H*W

# ================================= create convolution layer ==================================

# ================ 2d
# flag = 1
flag = 0
if flag:
    conv_layer = nn.Conv2d(3, 1, 3)   # input:(i, o, size) weights:(o, i , h, w)
    # 初始化卷积层权值
    nn.init.xavier_normal_(conv_layer.weight.data)
    # nn.init.xavier_uniform_(conv_layer.weight.data)

    # calculation
    img_conv = conv_layer(img_tensor)

# ================ transposed
flag = 1
# flag = 0
if flag:
    conv_layer = nn.ConvTranspose2d(3, 1, 3, stride=2)   # input:(input_channel, output_channel, size)
    # 初始化网络层的权值
    nn.init.xavier_normal_(conv_layer.weight.data)

    # calculation
    img_conv = conv_layer(img_tensor)

# ================================= visualization ==================================
print("卷积前尺寸:{}\n卷积后尺寸:{}".format(img_tensor.shape, img_conv.shape))
img_conv = transform_invert(img_conv[0, 0:1, ...], img_transform)
img_raw = transform_invert(img_tensor.squeeze(), img_transform)
plt.subplot(122).imshow(img_conv, cmap='gray')
plt.subplot(121).imshow(img_raw)
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

转置卷积前后图片显示如下，左边原图片的尺寸是 (512, 512)，右边转置卷积后的图片尺寸是 (1025, 1025)。

转置卷积后的图片一般都会有棋盘效应，像一格一格的棋盘，这是转置卷积的通病。

关于棋盘效应的解释以及解决方法，推荐阅读Deconvolution And Checkerboard Artifacts。