不正经

这个屌丝很懒，什么也没留下！

热门标签

数据结构第四章（串、数组和广义表）

作者：不正经 | 2024-04-09 15:14:55

踩

数据结构第四章（串、数组和广义表）

写在前面：

本系列笔记主要以《数据结构（C语言版）》为参考（本章部分图片来源于王道），结合下方视频教程对数据结构的相关知识点进行梳理。所有代码块使用的都是C语言，如有错误欢迎指出。
视频链接：第01周a--前言_哔哩哔哩_bilibili

一、串

1、串的定义

（1）串或字符串是由零个或多个字符组成的有限序列，用双引号在序列的两端进行标识。

（2）串中的数目称为串的长度，零个字符的串称为空串。

（3）串中任意个连续的字符组成的子序列称为该串的子串，包含子串的串相应地称为主串。通常称字符在序列中的序号为该字符在串中的位置，子串在主串中的位置则以子串的第一个字符在主串中的位置来表示。

（4）当且仅当两个串的值相等，称这两个串是相等的，也就是说，只有当两个串的长度相等且各个对应位置的字符都相等时两个串才相等。

（5）在各种应用中，空格常常是串的字符集合中的一个元素，因而可以出现在其它字符中间。由一个或多个空格组成的串" "称为空格串（用“Ø”表示，此处不是空串），其长度为串中空格字符的个数。

（6）串的逻辑结构和线性表极为相似，区别仅在于串的数据对象约束为字符集。然而，串的基本操作和线性表有很大差别：在线性表的基本操作中，大多以“单个元素”作为操作对象；而在串的基本操作中，通常以“串整体”作为操作对象，例如在串中查找某个子串，求取一个子串，在串的某个位置上插入一个子串，以及删除一个子串等。

2、串的存储结构和基本操作

（1）串的顺序存储：

①类似于线性表的顺序存储结构，用一组地址连续的存储单元存储串值的字符序列。按照预定义的大小，为每个定义的串变量分配一个固定长度的存储区，则可用定长数组描述如下：


#define MAXLEN 255   //串的最大长度
 
typedef struct
{
	char ch[MAXLEN + 1];   //存储串的一维数组（数组的0号元素不用）
	int length;            //串的当前长度（实际上串的长度可借助strlen函数求得）
}SString;

②多数情况下，串的操作是以串的整体形式参与的，串变量之间的长度相差较大，在操作中串值长度的变化也较大，于是可以根据实际需要，在程序执行过程中动态地分配和释放字符数组空间，若分配成功，则返回一个指向起始地址的指针作为串的基址，同时为了以后处理方便，约定串长也作为存储结构的一部分。这种字符串的存储方式也称为串的堆式顺序存储结构，定义如下：


#define MAXLEN 255
 
typedef struct
{
	char *ch;              //若是非空串，则按串长分配存储区，否则指针为NULL
	int length;            //串的当前长度
}HString;

（2）串的链式存储：

①由于串结构的特殊性——结构中的每个数据元素是一个字符，则在用链表存储串值时，存在一个“结点大小”的问题，即每个结点可以存放一个字符，也可以存放多个字符。当结点大小大于1时，由于串长不一定是结点大小的整倍数，则链表中的最后一个结点不一定全被串值占满，此时通常补上“#”或其它的非串值字符（通常“#”不属于串的字符集，是一个特殊的符号）。

②为了便于进行串的操作，当以链表存储串值时，除头指针外，还可附设一个尾指针指示链表中的最后一个结点，并给出当前串的长度。称如此定义的串存储结构为块链结构，说明如下：


#define CHUNKSIZE 80
 
typedef struct CHUNK
{
	char ch[CHUNKSIZE];
	struct CHUNK *next;
}CHUNK;
typedef struct
{
	CHUNK *head, *tail;   //串的头指针和尾指针
	int length;           //串的当前长度
}LString;

③串值的链式存储结构对某些串操作，如连接操作等有一定方便之处，但总的来说不如顺序存储结构灵活，它占用存储量大且操作复杂。

（3）串的一些基本操作如下所示，由于比较简单，在C语言系列中也有介绍过部分，且和顺序表及单链表的一些操作非常相似，故这里不再赘述。

3、串的模式匹配法

（1）子串的定位运算通常称为串的模式匹配或串匹配，此运算的应用非常广泛，比如在搜索引擎、拼写检查、语言翻译、数据压缩等应用中，都需要进行串匹配。设有两个字符串S和T，设S为主串（也称正文串），设T为子串（也称为模式），在主串S中查找与模式T相匹配的子串，如果匹配成功，确定相匹配的子串中的第一个字符在主串S中出现的位置。

（2）BF算法：

①算法步骤：

[1]分别利用计数指针i和j指示主串S和模式T中当前正待比较的字符位置，i初值为pos，初值为1。

[2]如果两个串均未比较到串尾，即i和j均分别小于等于S和T的长度时，则循环执行以下操作：

#1 S.ch[i]和T.ch[j]比较，若相等，则i和j分别指示串中下个位置，继续比较后续字符。

#2 若不相等，指针后退重新开始匹配，从主串的下一个字符（i= i- j+ 2）起再重新和模式的第一个字符（j=1）比较。

[3]如果j > T.length，说明模式T中的每个字符依次和主串S中的一个连续的字符序列相等，则匹配成功，返回和模式T中第一个字符相等的字符在主串S中的序号（i-T.length），否则称匹配不成功，返回0。

②算法实现：


int Index_BF(SString S, SString T, int pos)
{
	int i = pos, j = 1;   //初始化计数指针
	while (i <= S.length && j <= T.length)  //两个串均未比较到串尾
	{
		if (S.ch[i] == T.ch[j])  //未遇到不相同的字符，继续比较，如果比较到其中一个字符串结束，结束比较
		{
			i++; j++;
		}
		else   //遇到不相同的字符，指针后退，重新开始匹配
		{
			i = i - j + 2; j = 1;
		}
		if (j > T.length)  //计数指针j的值大于子串长度，说明子串的所有字符都和主串中的字符比较过，匹配成功
			return i - T.length;  //返回和模式T中第一个字符相等的字符在主串S中的序号
		else               //匹配失败
			return 0;
	}
}

③举例：模式T="abcac"和主串S的匹配过程（pos=1）。

④设主串的长度为n，子串的长度为m。最好情况下，每趟不成功的匹配都发生在模式串的第一个字符与主串中相应字符的比较，平均时间复杂度是O(n+m)；最坏情况下，每趟不成功的匹配都发生在模式串的最后一个字符与主串中相应字符的比较，平均时间复杂度是O(n×m)。

（3）KMP算法：

①KMP算法可以在O(n+m)的时间数量级上完成串的模式匹配操作。KMP算法在比较字符串的过程中，每当一趟匹配过程中出现字符不等时，无须回溯主串的指针，而是利用已经得到的“部分匹配”的结果将模式向右“滑动”尽可能远的一段距离后，继续进行比较。

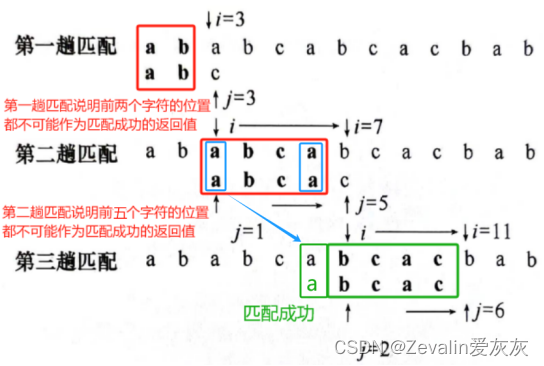
②假设主串为" $s_{1}s_{2}\cdots s_{n}$ "，子串为" $t_{1}t_{2}\cdots t_{n}$ "，若令next[j]= k，则next[j]表明当模式中第j个字符与主串中相应字符“失配”时，在模式中需重新和主串中该字符进行比较的字符的位置，由此可引出模式串的next函数的定义为：

[1]next数组的手算方法：当第j个字符匹配失败，由前1~j-1个字符组成的串记为S，则next[j]=S的最长相等前后缀长度+1，前后缀可以有重叠，但不能覆盖全串；特别地，next[1]=0。（串的前缀指包含第一个字符，且不包含最后一个字符的子串；串的后缀指包含最后一个字符，且不包含第一个字符的子串）

[2]举例（计算next数组不需要关心主串）：

j	1	2	3	4	5	6	7	8
模式串	a	b	a	a	b	c	a	c
next[j]	0	1	1	2	2	3	1	2
计算过程	#1	#2	#3	#4	#5	#6	#7	#8

#1 固定有next[1]=0。

#2 S串的前缀和后缀均为空串，next[2]=0+1=1。

#3 S="ab"，前缀和后缀没有相等的子串，next[3]=0+1=1。

#4 S="aba"，前缀子串"a"和后缀子串"a"相等，next[4]=1+1=2。

#5 S="abaa"，前缀子串"a"和后缀子串"a"相等，next[5]=1+1=2。

#6 S="abaab"，前缀子串"ab"和后缀子串"ab"相等，next[6]=1+2=3。

#7 S="abaabc"，前缀和后缀没有相等的子串，next[7]=0+1=1。

#8 S="abaabca"，前缀子串"a"和后缀子串"a"相等，next[8]=1+1=2。

③利用模式的next函数进行匹配的过程示例：

④KMP算法的代码实现：

[1]计算next数组：


void get_next(SString T, int next[])
{
	int i = 1, j = 0;
	next[1] = 0;
	while (i < T.length)
	{
		if (j == 0 || T.ch[i] == T.ch[j])
		{
			i++;
			j++;
			next[i] = j;
		}
		else
		{
			j = next[j];
		}
	}
}

[2]算法核心部分：


int Index_KMP(SString S, SString T, int pos)
{
	int i = pos, j = 1;   //初始化计数指针
	int *next = (int*)malloc(sizeof(int)*T.length);
	get_next(T, next);    //计算next数组
	while (i <= S.length && j <= T.length)  //两个串均未比较到串尾
	{
		if (j == 0 || S.ch[i] == T.ch[j])  //继续比较后面的字符，直到比较至一个串结束
		{
			i++;
			j++;
		}
		else
		{
			j = next[j];    //模式串向右移动
		}
	}
	if (j > T.length)  //计数指针j的值大于子串长度，说明子串的所有字符都和主串中的字符比较过，匹配成功
		return i - T.length;  //返回和模式T中第一个字符相等的字符在主串S中的序号
	else               //匹配失败
		return 0;
}

⑤KMP算法优化：当子串和模式串不匹配时，主串指针i不回溯，模式串指针j=nextval[j]，nextval数组的求法如下：

[1]先求出next数组。

[2]当j等于1时，nextval[j] 赋值为0，作为特殊标记。

[3]当j大于1时，分两种情况：


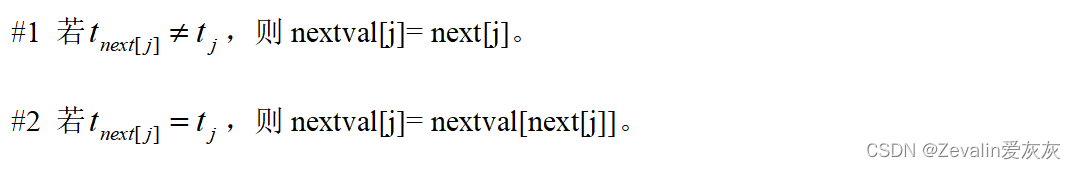
void get_nextval(SString T, int nextval[])
{
	int i = 1, j = 0;
	nextval[1] = 0;
	while (i < T.length)
	{
		if (j == 0 || T.ch[i] == T.ch[j])
		{
			i++;
			j++;
			if (T.ch[i] != T.ch[j])
				nextval[i] = j;
			else
				nextval[i] = nextval[j];
		}
		else
		{
			j = nextval[j];
		}
	}
}

二、数组

1、数组的类型定义

（1）数组是由类型相同的数据元素构成的有序集合，每个元素称为数组元素，每个元素受n（n≥1）个线性关系的约束，每个元素在n个线性关系中的序号称为该元素的下标，可以通过下标访问该数据元素。

（2）因为数组中每个元素处于n（n≥1）个关系中，故称该数组为n维数组。数组可以看成线性表的推广，其特点是结构中的元素本身可以是具有某种结构的数据，但属于同一数据类型。

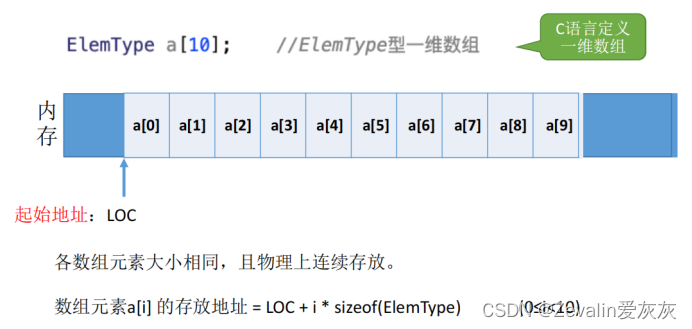
（3）关于数组在C语言的笔记中已经有详细的介绍和应用示例，且操作简单，这里不再过多赘述。

2、特殊矩阵的压缩存储

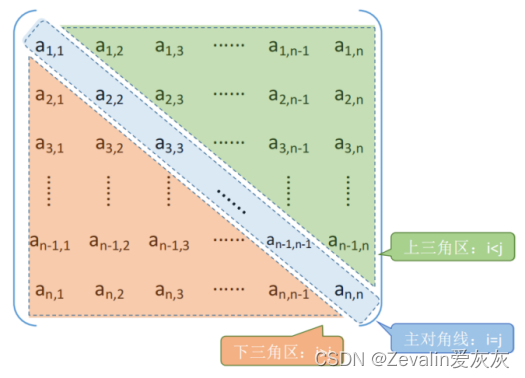
（1）在数值分析中经常出现一些阶数很高的矩阵，同时在矩阵中有很多值相同的元素或者是零元素，有时为了节省存储空间，可以对这类矩阵进行压缩存储。所谓压缩存储，是指为多个值相同的元只分配一个存储空间，对零元不分配空间。假若值相同的元素或者零元素在矩阵中的分布有一定规律，则称此类矩阵为特殊矩阵，特殊矩阵主要包括对称矩阵、三角矩阵和对角矩阵等。

（2）对称矩阵：

①若n阶矩阵A中的元满足 $a_{ij}=a_{ji} \; \: \left ( 1\leq i,j\leq n \right )$ ，则称A为n阶对称矩阵。

②对于对称矩阵，可以为每一对对称元分配一个存储空间，则可将 $n^{2}$ 个元压缩到 $n(n+1)/2$ 个元空间中。不失一般性，可以行序为主序存储其下三角（包括对角线）中的元。

③假设以一维数组B[n (n+1) /2]作为n阶对称矩阵A的存储结构，则B[k]和矩阵元 $a_{ij}$ 之间存在着一一对应的关系，任意给定的一组下标(i, j)均可在B中找到矩阵元 $a_{ij}$ ，反之亦然。

（3）三角矩阵：

①以对角线划分，三角矩阵有上三角矩阵和下三角矩阵两种。上三角矩阵是指矩阵下三角（不包括对角线）中的元均为常数c或0的n阶矩阵，下三角矩阵与之相反。对三角矩阵进行压缩存储时，除了和对称矩阵一样，只存储其上（下）三角中的元素之外，再加一个存储常数c的存储空间即可。

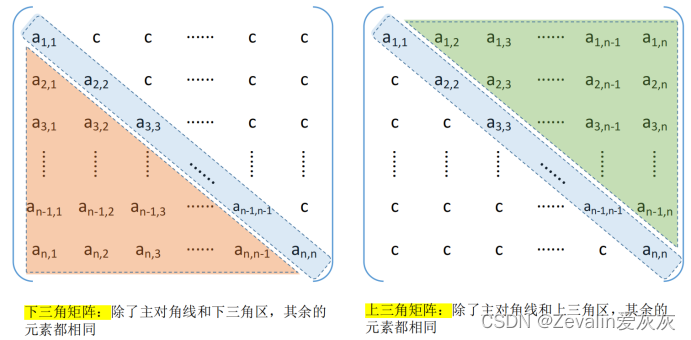
②下三角矩阵的B[k]和矩阵元之间的对应关系如下。

③上三角矩阵的B[k]和矩阵元之间的对应关系如下。

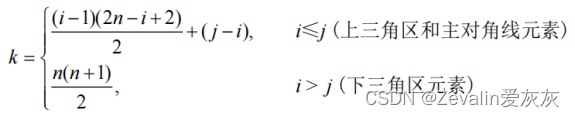
（4）对角矩阵（带状矩阵）：

对角矩阵所有的非零元都集中在以对角线为中心的带状区域中，即除了对角线上和直接在对角线上、下方若干条与对角线平行的线上的元之外，所有其它的元皆为零。对这种矩阵，也可按某个原则（或以行为主，或以线的顺序）将其压缩存储到一维数组上。

（5）稀疏矩阵：

①稀疏矩阵是非零元较零元少，且分布没有一定规律的矩阵。对稀疏矩阵，有三元组顺序表法和十字链表法两种压缩方法。

②三元组顺序表法（有序的双下标法）：用三元组确定每个非零元，三元组存各非零元的值、行列位置，通常还加一组存矩阵总行数、总列数及非零元素总个数。

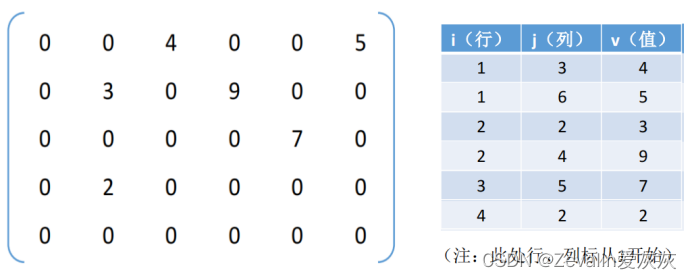
[1]优点：非零元在表中按行序有序存储，因此便于进行依行序顺序处理的矩阵运算。

[2]缺点：不能随机存取，若按行号存取某一行中的非零元，需要从头开始进行查找。

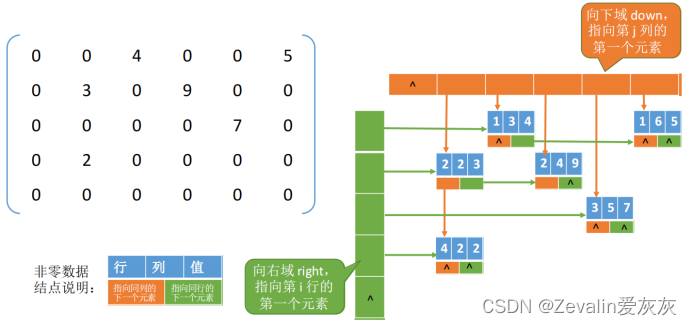
③十字链表法：矩阵的每一个非零元用一个结点表示，该结点除了存储非零元的值、行列位置以外，还要有两个域——right和down，right用于连接同一行中的下一个非零元（没有则为NULL），down用于连接同一列中的下一个非零元（没有则为NULL）。

三、广义表

1、广义表的定义

（1）广义表是线性表的推广，也称为列表，一般记作 $LS=(a_{1},a_{2},\cdots ,a_{n})$ ，其中LS是广义表 $(a_{1},a_{2},\cdots ,a_{n})$ 的名称。在广义表的定义中， $a_{i}$ 可以是单个元素，也可以是广义表，分别称为广义表LS的原子和子表。习惯上，用大写字母表示广义表的名称，用小写字母表示原子。

（2）广义表的数据元素具有相对次序，除了第一个元素和最后一个元素外，都有一个直接前驱和一个直接后继。

2、广义表的几个重要结论

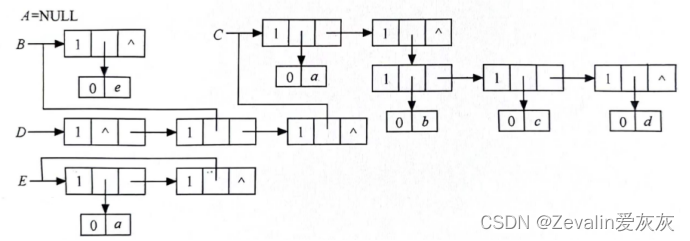
（1）一些广义表的例子：

①A=() ——A是一个空表，其长度为0（长度定义为最外层所包含的元素个数）。

②B=(e) ——B只有一个原子e，其长度为1。

③C=(a,(b,c,d)) ——C的长度为2，两个元素分别为原子a和子表(b,c,d)。

④D=(A,B,C) ——D的长度为3，3个元素都是广义表，显然，将子表的值代入后，则有D=((),(e),(a, (b, c,d)))。

⑤E=(a,E) ——这是一个递归的表，其长度为2，E相当于一个无限的广义表。

（2）广义表的元素可以是子表，而子表的元素还可以是子表……由此，广义表是一个多层次的结构，可以用图形象地表示。广义表的深度定义为该广义表展开后所含括号的重数，如上面例子中的C、E深度为2，D深度为3，A、B深度为1（空表的深度也为1）。

（3）广义表可为其它广义表所共享，例如在上述例子中，广义表A、B和C为D的子表，则在D中可以不必列出子表的值，而是通过子表的名称来引用。

（4）广义表可以是一个递归的表，即广义表也可以是其本身的一个子表，例如表E就是个递归的表。

3、广义表的两个重要操作

（1）取表头GetHead(LS)：取出的表头为非空广义表的第一个元素，它可以是一个单原子，也可以是一个子表（甚至可能是一个空表，如上述例子中的D）。

（2）取表尾GetTail(LS)：取出的表尾为除去表头之外由其余元素构成的表，即表尾一定是一个广义表（除去表头后没有剩余元素的话，表尾是一个空表）。

4、广义表的头尾链表存储结构

（1）由于广义表中的数据元素可能为原子或广义表，因此需要两种结构的结点：一种是表结点，用以表示广义表；一种是原子结点，用以表示原子。

（2）若广义表不为空，则可分解成表头和表尾，因此，一对确定的表头和表尾可唯一确定广义表。一个表结点可由3个域组成——标志域、指示表头的指针域和指示表尾的指针域，原子结点只需两个域——标志域和值域，其中标志域值为1时表明结点是子表，值为0时表明结点是原子。

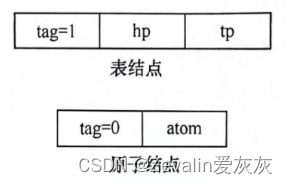
（3）广义表的头尾链表存储表示：


typedef int AtomType;   //以整型为例
typedef enum
{
	ATOM,  //ATOM == 0，表示原子
	LIST   //LIST == 1，表示子表
}ElemTag;
typedef struct GLNode
{
	ElemTag tag;    //公共部分，用于区分原子结点和表结点
	union           //原子结点和表结点的联合部分
	{
		AtomType atom;  //结点的值域
		struct          //表结点的指针域
		{
			struct GLNode *hp, *tp;  //指向表头和表尾的指针
		}ptr;
	};
}*GList;

（4）上述例子中的几个广义表存储结构如下所示，除空表的表头指针为空外，对任何非空广义表，其表头指针均指向一个表结点，且该结点中的hp域指向广义表表头（或为原子结点，或为表结点），tp域指向广义表表尾（除非表尾为空，则指针为空，否则必为表结点）。

四、算法设计举例（未使用自定义的数据结构）

1、例1

（1）问题描述：设计一个算法统计在输入字符串中各个不同字符出现的频度，并将结果存入文件（字符串中的合法字符为A~Z这二十六个字母和0~9这十个数字）。

（2）代码：


void T1(void)
{
	char str[300];
	scanf("%s", str);
	int i = 0;
	int record[36] = { 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0 };
	while (str[i])
	{
		if ((str[i] >= 'A'&&str[i] <= 'Z'))
		{
			record[(int)(str[i] - 'A')]++;
		}
		if ((str[i] >= '0'&&str[i] <= '9'))
		{
			record[(int)(str[i] - '0'+ 26)]++;
		}
		i++;
	}
	FILE* pFile;
	pFile = fopen("str.txt", "w");
	if (pFile == NULL)
	{
		return;
	}
	fprintf(pFile, "字符串：%s\n", str);
	for (int j = 0; j < 36; j++)
	{
		if (j < 26)
		{
			printf("字符“%c”的个数为：%d\n", 'A' + j, record[j]);
			fprintf(pFile, "字符“%c”的个数为：%d\n", 'A' + j, record[j]);
		}
		else
		{
			printf("字符“%c”的个数为：%d\n", '0' + j - 26, record[j]);
			fprintf(pFile, "字符“%c”的个数为：%d\n", '0' + j - 26, record[j]);
		}	
	}
	//关闭文件
	fclose(pFile);
}

2、例2

（1）问题描述：设计一个递归算法来实现字符串逆序存储，要求不令设串存储空间。

（2）代码：


void T2(char* str ,int len)
{
	int left = 0;
	int right = len - 1;
	if (left <= right)
	{
		char c = str[left];
		str[left] = str[right];
		str[right] = c;
		str++;
		T2(str, right - 1);
	}
	return;
}

3、例3

（1）问题描述：设计算法，将字符串t插入到字符串s中，插入位置为pos（假设分配给字符串s的空间足够让字符串t插入，不使用库函数）。

（2）代码：


void T3(char* t ,char* s ,int pos)
{
	if (pos < 0)
	{
		printf("参数位置非法！\n");
		return;
	}
	int i = 0;
	int j = 0;
	char* sp = s;
	char* tp = t;
	while (*sp)
	{
		sp++;
		i++;
	}
	while (*tp)
	{
		tp++;
		j++;
	}
	if (i < pos)
	{
		printf("参数位置不合理！\n");
		return;
	}
	int a = pos;
	while (s[a - 1])
	{
		s[a + j] = s[a];
		a++;
	}
	while (*t)
	{
		s[pos] = *t;
		t++;
		pos++;
	}
}

4、例4

（1）问题描述：已知字符串s1中存放一段英文，设计算法将其按给定的长度n格式化成两端对齐的字符串s1（长度为n且首尾不得为空格字符），多余的字符送s3。

（2）代码：


void T4(char* s1 ,char* s2 ,char* s3 ,int n)
{
	char* p1 = s1;
	char* p2 = s2;
	char* p3 = s3;
	while (*p1)
	{
		if (*p1 != ' ')
		{
			*p2 = *p1;
			p2++;
			n--;
		}
		p1++;
		if (!n)
			break;
	}
	while (*p1)
	{
		if (*p1 != ' ')
		{
			*p3 = *p1;
			p3++;
		}
		p1++;
	}
	*p2 = '\0';
	*p3 = '\0';
}

5、例5

（1）问题描述：设计一个算法判断二维数组a中所有元素是否互不相同，输出结果，分析时间复杂度。

（2）代码：


void T5(int a[2][2] ,int n)
{
	int* p = (int*)a;
	while (n - 1)
	{
		if (*p == *(p + 1))
		{
			printf("数组a中元素不是互不相同！\n");
			return;   //时间复杂度取决于数组a的情况，最坏情况下时间复杂度为O(n)，其中n为数组元素个数
		}
		p++;
		n--;
	}
	printf("数组a中元素互不相同！\n");
	return;
}

6、例6

（1）问题描述：设任意n个整数存放于数组A中，设计算法将所有正数排在所有负数前面，要求时间复杂度为O(n)。

（2）代码：


void T6(int a[10], int n)
{
	int left = 0;
	int right = n - 1;
	while (left <= right)
	{
		if (a[left] <= 0 && a[right] > 0)
		{
			int tmp = a[left];
			a[left] = a[right];
			a[right] = tmp;
			left++;
			right--;
		}
		else if (a[left] <= 0 && a[right] <= 0)
			right--;
		else if (a[left] > 0 && a[right] > 0)
			left++;
		else if (a[left] >= 0 && a[right] < 0)
		{
			left++;
			right--;
		}
	}
}

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/不正经/article/detail/393584

数据结构 第四章（串、数组和广义表）

一、串

1、串的定义

2、串的存储结构和基本操作

3、串的模式匹配法

二、数组

1、数组的类型定义

2、特殊矩阵的压缩存储

三、广义表

1、广义表的定义

2、广义表的几个重要结论

3、广义表的两个重要操作

4、广义表的头尾链表存储结构

四、算法设计举例（未使用自定义的数据结构）

1、例1

2、例2

3、例3

4、例4

5、例5

6、例6

数据结构第四章（串、数组和广义表）