- 1【智能家居】智能家居项目
- 2AR眼镜——Vuzix Blade填坑笔记_vuzix blade链接手机
- 3大模型训练资源评估_大模型算力评估
- 4nginx和keepalived 集群实现在centos8简单部署命令_centos8 keepalived nginx
- 5unity标准Shader之四大渲染模式_unity shadering mode
- 6Git学习笔记(第8章):IEAD实现GitHub操作(VSCode)_vscode 登录github账号
- 7数据结构 —— Dijkstra算法
- 8chatgpt赋能python:Python波动方程介绍:掌握物理模型与实际应用_python在建立物理模型中的应用
- 9Vue的学习之数据与方法
- 10云知声小小智慧工牌,构建销售智慧管理“大格局”_智能分析管理后台管理首页
Graph Embedding_有向图 节点相似度计算
赞
踩
目录
LINE(large-scale Information Network Embedding)(有向图无向图都可)
对于图节点的向量表示,有one-hot向量的方式,即n个n维向量。但是使用这种方式,首先,如果节点的个数有很多,那么节点的向量表示就会占用很大空间,其次,one-hot向量表示不能表现出节点之间图上的关系,所以引入了Graph Embedding,优点在于首先简化了节点表市长度,其次是能够表示出节点之间图上的关系信息。
Deepwalk(适用于无向图)
采用随机游走(Random Work)的方式得到图上的信息,随机游走的思想:首先给定一个节点,可以按照与节点相连的边进行的随机游走,到达下一个顶点以后就随机选择一条边,进行下一次的随机游走,通过这样的方式就能得到每个随机游走的节点的序列,在对每个节点进行多次的随机游走,就得到了图上面节点的序列,再定义一个窗口,通过P(窗口大小的所有节点|某个节点的embedding)就能得到节点的Embedding。
算法如下:
w:定义给定节点向前或者向后是多少步,计算这个范围的节点的值:(在给定V4的embedding的情况下,计算V2,V3,V5,V6同时出现的概率)通过这种方式最终能够得到所有节点的embedding的表示。
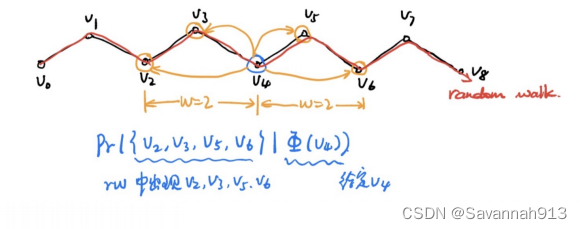
d:定义embedding的大小是多少
γ:定义每个节点的循环次数
t:定义步长——walk length
循环γ次,对节点进行打乱,对于G中每个节点i进行随机游走t步,就得到了一个随机游走的序列,对这个序列以及事先定义好的graph embedding和随机游走序列,以及窗口大小通过SkipGram的方法学习graph embedding。

graph embedding是无监督的训练方式,如何判断训练好坏?
首先给定一张图,并且事先知道它每个节点的label值,此时通过无监督的方式训练每个节点的embedding,训练完成之后,把节点的embedding当做特征,把它输入到分类器中,根据它产生的label我们就知道了分类器的好坏,而这个分类器的好坏就能表示出计算出的embedding的好坏。
LINE(large-scale Information Network Embedding)(有向图无向图都可)
在比较大的图上做embedding,能够使得效果比较好。
一阶相似性:如果两个节点相连接,而且这两个节点的边的权重比较大,那么这两个节点是很相似的。
二阶相似性:如果两个节点的邻居是很相似的,那么这两个节点即使不连接也是很相似的。
如果图中节点的度比较低,也就是节点连接的邻居比较少,那么用LINE求解邻居相似性,就不会达到特别好的效果。
一阶相似性
先初始化所有节点的embedding,即,那么节点i和节点j的联合概率分布就可以求得,以节点6和节点7为例:(sigmoid函数)
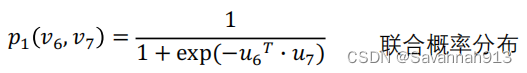
节点6和节点7的经验概率分布可以表示为,节点6和节点7相连接的边的权重除以图上面所有边的权重。

得到两个节点的联合概率分布和经验概率分布之后,下一步需要求解两种概率分布的距离,用到的是KL散度。
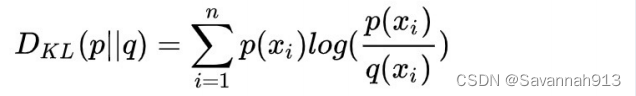
举个求解KL散度的例子:
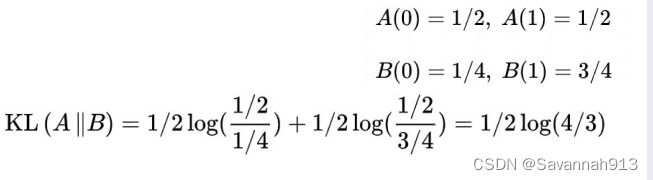
而在我们所研究的联合概率分布和经验概率分布中的KL散度:二者的KL散度
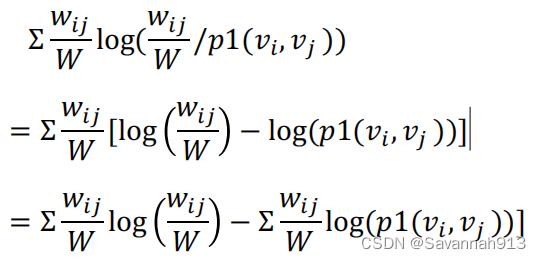
由于上述KL散度化简后,第一项是边之间的权重,是固定的,所以计算loss的时候不需要,第二项的W也是,所以原式能够化简为
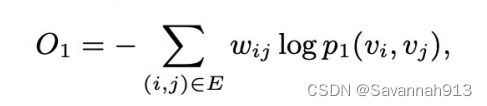
而训练的目的就是使得这个距离最小,把这个距离当做loss函数,这样就能学到最终embedding的表示。
二阶相似性
定义每个节点有两个向量表示,第一个向量表示是节点本身的向量表示,第二个向量表示是该节点作为其他向量邻居的向量表示
。
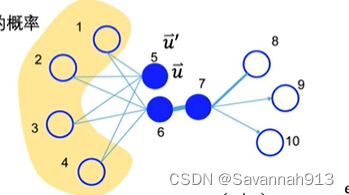
求条件概率:给定时,
的概率公式,在做一个归一化操作:
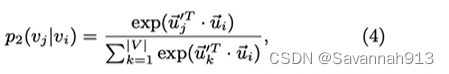
求经验概率:节点i和节点j相连的边的权重除以节点i的出度的边的权重之和:
举个例子:
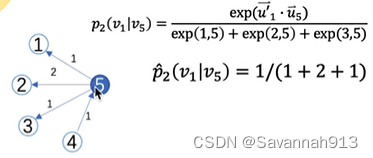
求上述两个概率的KL散度
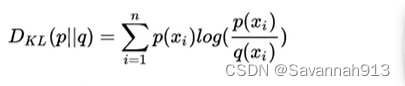
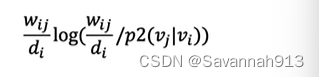
对于上面这个式子,为其增加一个控制节点重要性的因子,而且使得
=
,那么此时,在去电对loss函数不影响的值,将原来的KL散度作为loss函数就可以写为:
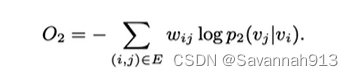
仍然将节点原来的表示作为节点的二阶embedding表示。将一阶和二阶embedding训练结束之后,需要将二者组合成一个embedding。通常采用直接拼接的方式将二者组合。
Node2vec
同质性(homophily):距离相近节点的embedding应该尽量近似,节点u与其相连的节点s1、s2、s3、s4的embedding表达应该是接近的,这就是“同质性“的体现。
结构等价性(structural equivalence):结构上相似的节点的embedding应该尽量接近,节点u和节点s6都是各自局域网络的中心节点,(连接两个簇的中间节点)结构上相似,其embedding的表达也应该近似,这是“结构性”的体现。
关于Node2vec算法中Graph Embedding同质性和结构性的进一步探讨 - 知乎 (zhihu.com)
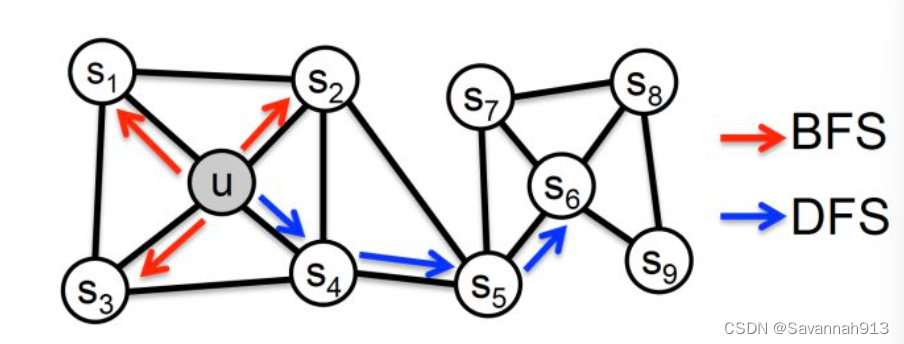
Node2vec和deepwalk一样也是一种游走的方法,但是Node2vec是一种有策略的游走方法。如下图所示,从节点t走到节点v之后,下一个节点有t,,其中,变标签表示搜索偏差α,此时用(v,x)表示要走的下一步,用
表示游走到那个边上的可能性,
,其中,
表示边的权重,重点是
,公式如下:
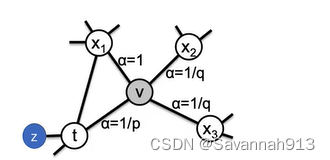
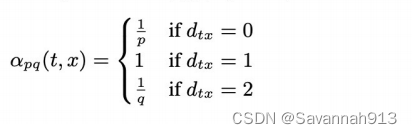
在公式中,
=0指的是,距离t节点为0的节点,即从t节点到达v节点之后,又重新到达t节点这个α是
,
=1指的是,距离t节点为1的节点(节点z和节点
),即走向t节点或者是走向z节点的α是1,
=2指的是,到达距离t节点为2的节点(节点x2和节点x3)的α是
。
计算游走到下一个节点的可能性:
t节点在又走到了v节点之后,下一步游走到z的可能性为0,因为,节点v和节点z不相连,所以=0。t节点在又走到了v节点之后,下一步走到t的可能性:
,其他路径如下:

算法表示:

这个梯度下降算法就是,在给定u的情况下,计算周围邻居节点出现的概率。取使得该概率最大值的embedding
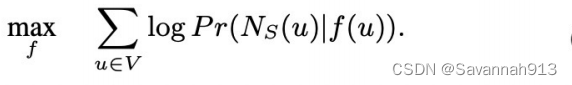
pq值对结果的影响

Struc2vec
之前的embedding都是基于近邻关系,但是有些节点没有近邻,也有相似的机构性。
定义距离信息
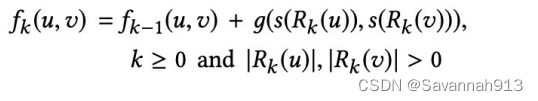

:表示节点u和节点v在k阶邻居下的距离
khop邻居表示k跳邻居。
S(s):集合S中每个元素的度的有序序列。
例子
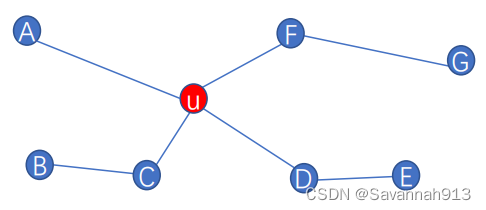
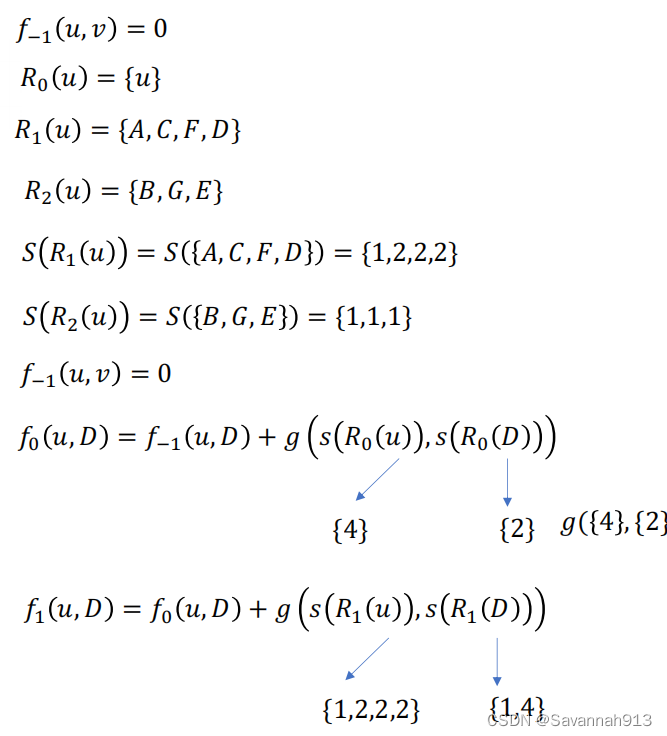
上述计算最终停留在计算g(s,s)中,先学习一个DTM动态时间规整算法:
动态时间规整算法DTM(求两个序列的距离)
如果直接求左图中两个两个线上的点的欧氏距离,结果就会很大,但是,如果按照虚线将对应的节点给对应好,那么两部分节点的距离就会等于0,这种距离计算方式就叫做动态时间规整,即通过不断压缩和拓展x轴,使得两个节点的距离最小,即动态时间规整算法DTM。表现在右侧矩阵上就是,按照值最小的点走,走到最后,所有经过点的加和最小就表示两个节点的动态时间规整计算出的距离。
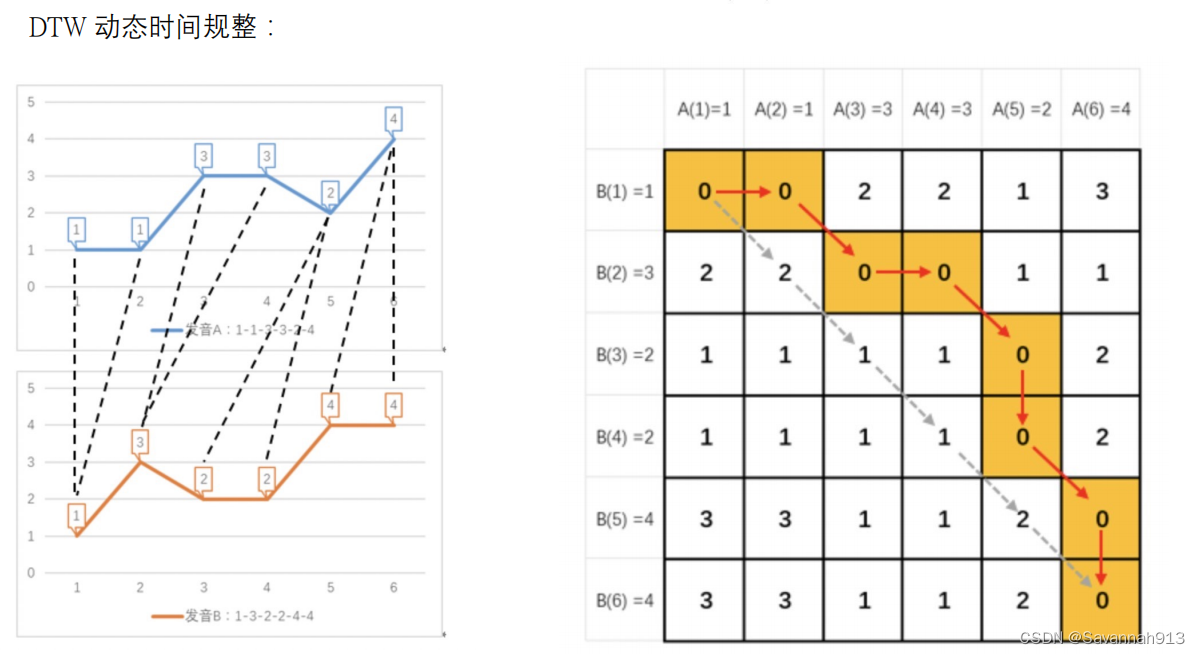
该算法在节点与节点之间的距离定义:
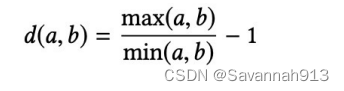
对于原来节点距离计算的
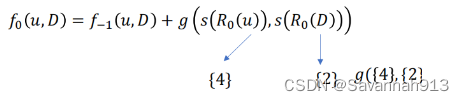
g(s(R(u)),s(R(d)))计算这两个节点的距离用上述公式表示为:(因为只有两个节点,最大值最小值很容易确定)
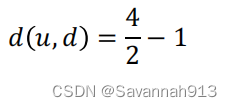
计算两个序列的距离:(采用动态时间规整的方式去计算)
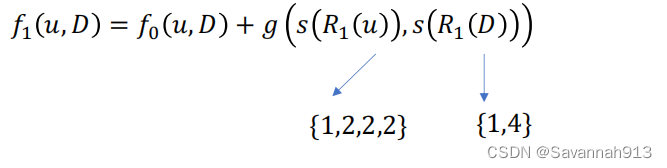
两个节点,他们的一阶邻居的度,二阶邻居的度比较相似,那么这两个节点的结构特点就是比较相似的。
对于结构相似性的计算,是通过计算两个节点在一阶邻居下的距离和二阶邻居下的距离,两个距离比较相近,那么这两个节点就有较强的结构相似性。
构建多层带权重图
节点两两连接,两两之间相似度。eg:0跳邻居下5个节点,计算这5个节点的相互之间的相似性就构成了一个全连接图,对每个边的权重的定义:
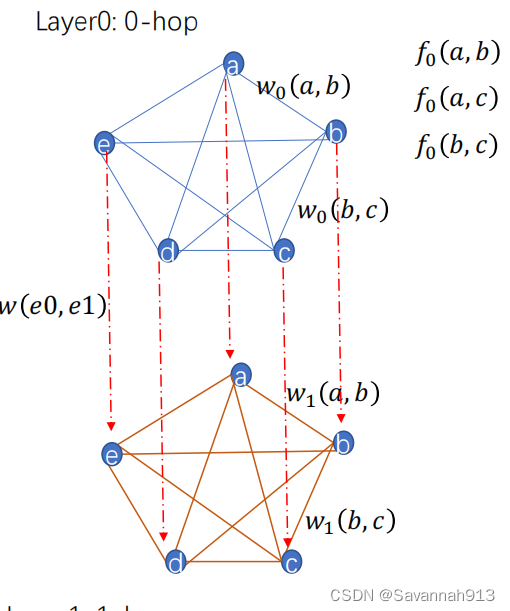
![]()
层与层之间连接的边的权重:
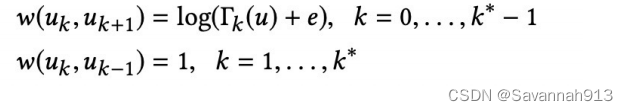
对于其中的定义如下:
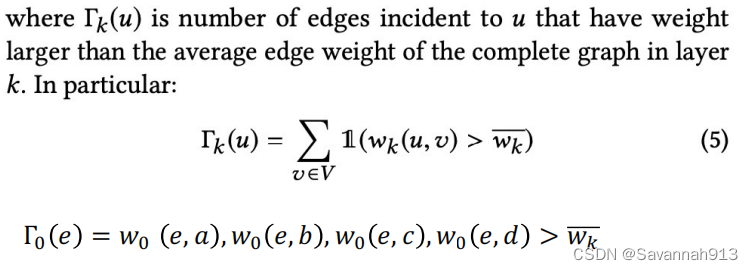
对于上面图片上的例子,简单来说就是,与节点e相连的边的权重,有几个大于他们平均权重的那么就是多少。
顶点采样序列
进行下一次采样时,有p的概率在本层游走,有1-p的概率字上下游切换。本层游走就是指,某一个节点a到达本层其他节点的概率是多少,计算方法如下:
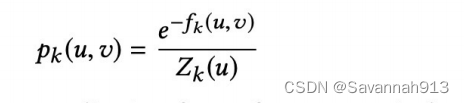
就是每条边上的权重,如上面一个直观图所示,
,分母
就是对所有边的权重进行求和。
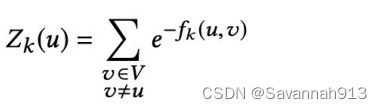
那么,上下游切换的节点概率的计算:
我们之前计算出来了对上层游走和下层游走的权重:(第一个式子是下一层,第二个式子是上一层,显然,到下一层游走的权重是大于等于1的,所以一般是向下一层游走)
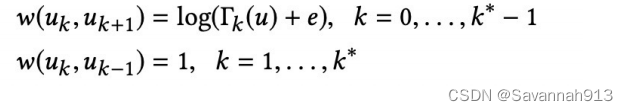
那么到上层游走和下层游走的概率为:
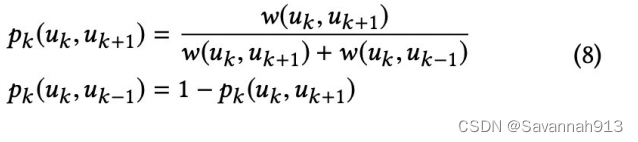
最后,使用skip-gram的方式就能生成embedding了。

Struc2ves适用于节点分类问题中(其结构标识比邻居标识更重要的时候,此时采用Struc2vec)
SDNE
之前的所有embedding方式都是浅层的结构,而浅层模型往往不能捕获高度非线性的网络结构,那么就产生了SDNE算法,使用多个非线性层来捕获node的embedding。
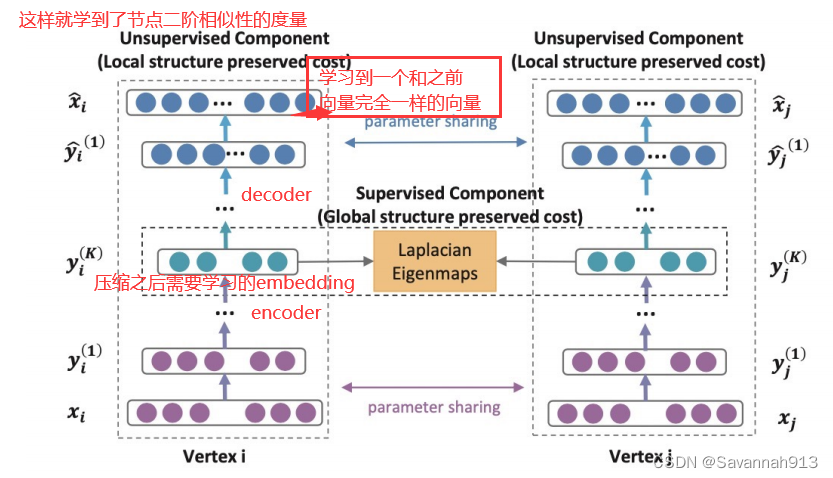
邻接矩阵的第i行表示i节点跟和它相连接的节点的关系,通过encoder压缩之后的embedding就包含了节点i邻域的表示,在通过decoder就能解出邻居的表示。这就考虑了节点间的二阶形似度。
loss函数表示:

如果是不连接的,那么
=1,否则(两个节点是连接的)就定义
的值为β(>0)
对于一阶相似性的捕获,如果节点i和节点j相连接的,那么计算两个节点embedding的误差需要最小。这就捕获了节点的一阶相似度,loss函数:
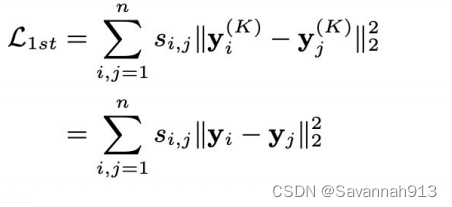
将上述一阶相似度误差和二阶相似度误差相结合,就得到了整体的loss函数:
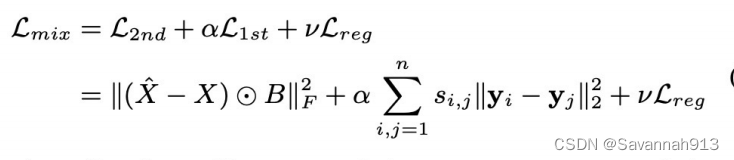
通过反向传播的方式学习模型的参数,进而求得embedding。(加上了L2正则)

总结:



