《程序设计解题策略》——1.2　利用最小生成树及其扩展形式解题

本节书摘来自华章计算机《程序设计解题策略》一书中的第1章，第1.2节,作者：吴永辉　王建德 更多章节内容可以访问云栖社区“华章计算机”公众号查看。

1.2　利用最小生成树及其扩展形式解题

设G=(V，E，ω)是连通的有权无向图(节点集为V，边集为E，边权集为ω)，连通图G中包含所有节点，且只有V-1条边的连通子图即为G的生成树。边权值和最小的生成树称为最小生成树。在现实生活中，最小生成树的原理和算法有着广泛的应用。程序设计竞赛中与最小生成树有关的试题一般有两类：
1) 构建最小生成树。
2) 应用最小生成树原理优化算法。
本节除了深入研讨最小生成树的性质和求解方法外，还给出了三种特殊类型生成树：
1) 最优比率生成树。
2) 最小k度限制生成树。
3) 次小生成树的解法。
1.2.1　最小生成树的思想和应用
我们先来探讨最小生成树的解法。设：
A是一棵最小生成树的子集，如果边(u，v)不属于A且A∪{(u，v)}仍然是某一棵最小生成树的子集，就称(u，v)为集合A的安全边。由此引出计算最小生成树的一般思想：　

（1） Prim算法
从任一节点出发，通过不断加入边权最小的安全边扩展最小生成树，直至连接了所有节点为止。图1.2-2列举了运用Prim算法计算最小生成树的过程。

显然，Prim算法采取了在一棵树上扩展的计算方式。如果用相邻矩阵w［］［］存储图、用一维数组key［］存储每个树外节点到树中节点的边所具有的最小权值(简称最短距离值)，用π［］记录生成树中每个节点的父亲，用队列Q存储树外节点，则可得到如下算法流程：

Void PRIM(G,w,r)　　　　　　　　// 图G的相邻矩阵为w，构造以r为根的最小生成树
{
Q=V［G］;// 所有节点送入队列Q
for（每个u∈Q）key［u］=∞// 所有节点的最短距离值初始化为∞
key［r］=0;// 根r的最短距离值为0
π［r］=NIL;// r的父节点为空,即r进入生成树
while(Q<>Ф）// 若队列不空
{ u=EXTRACT-MIN(Q);// 队列Q中距离值最小的节点u出队进入生成树
for（每个v∈Adj［u］）// 对Q中u相邻的每个节点v进行松弛操作：若v在队列Q且（u,v）的
// 边权小于原距离值，则v的父亲调整为u，距离值调整为（u,v）的边权
if(v∈Q)&&(w(u,v)<key［v］){π［v］=u;key［v］=w(u,v) };
}
}

如果队列Q采用一维数组存储，每次从Q中取出key值最小的节点，需要运行时间为O(V)；存在V次这样的操作，所以从Q中取key值最小节点的全部运行时间为O(V2)。对每个key值最小的节点来说，与之相邻的每个节点都要考察一次，因此考察次数为O(V)。而每确定一个节点进入生成树后，需要花费O(1)的时间更新与之相连的树外节点的key值，累计整个算法的运行时间为O(V2)；如果队列Q采用小根堆组存储，则算法的运行时间可降为O(V*log2V)。由此看出，Prim算法的时间复杂度取决于节点数V，而与边数E无关，因此一般适用于稠密图。
（2） Kruskal算法
按照权值从小到大的顺序排列边。初始时，每个节点单独组成了一棵生成树。然后按照权值递增顺序扩展安全边。每拓展一条安全边，将其中两棵生成树合并成一棵，直至构造出连接所有节点的一棵最小生成树为止。图1.2-3列举了运用Kruskal算法计算最小生成树的过程。

下面给出Kruskal算法的基本流程。

Void KRUSKAL(G,w)
{A=Ф　　　　　　　　　　　　　　　// 最小生成树的子集初始化为空
For(每个节点v∈V［G］)v自成一个集合；
根据边权递增的顺序排序边表E；
for（顺序搜索E中的每条边(u,v)）
{ if （u和v属于两个不同的集合）
{ A=A∪{(u,v);// (u,v)进入生成树A
合并u和v所在的两个集合；
}
}
return A;// 返回生成树A
}

显然，Kruskal算法采取了合并生成树的计算方式:初始化需占用时间O(V)，边按照边权递增顺序排序需要的运行时间为O(Elog2E)；对分离集的森林要进行O(E)次操作，每次操作需要时间O(log2E)，所以Kruskal算法的全部运行时间为O(Elog2E)。由于Kruskal算法的时间复杂度取决于边数E，而与节点数V无关，因此一般适用于稀疏图。
在竞赛中有不少构建最小生成树的试题，我们需要从无向图的具体结构和最小生成树的性质出发，运用各种算法在图中寻找属于最小生成树的边。这些题有些属于显性的最小生成树问题，有些虽不直接以最小生成树面貌出现，但可以借助最小生成树的原理化繁为简，化未知为已知。
【1.2.1　Arctic Network】
【问题描述】
国防部(The Department of National Defence，DND)要通过无线网络同几个北方的哨所进行通信。两种不同的通信技术将被用于建立网络：每个哨所拥有一台无线电收发报机以及其中一些哨所还拥有一个卫星频道。
任何两个拥有卫星频道的哨所，无论它们的位置在哪里，都可以通过卫星进行通信。否则，这两个哨所由于收发报机的功率，只有在它们之间的距离不超过D的情况下，通过无线电进行联络。D的值越高，就要用功率更高的收发报机，但这样成本非常高。出于采购和维修方面的考虑，哨所使用的收发报机必须是相同的；也就是说，对每一对哨所，D的值必须是相同的。
请你确定收发报机的最小D值。在每对哨所之间，必须至少有一条(直接或间接的)通信路径。
输入：
输入的第一行给出N，表示测试用例的个数。每个测试用例的第一行给出S和P，其中S表示卫星频道的数量，1≤S≤100；P表示哨所的数量，S＜P≤500。接下来给出P行，每行给出一个哨所的(x，y)坐标，以公里为单位(坐标是在0和10000之间的整数)。
输出：
对每个测试用例，输出一行，给出要连接网络的最小的D值，精确到小数点后2位。

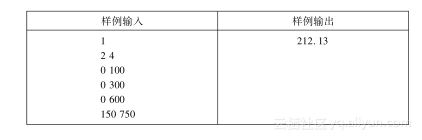
试题来源：Waterloo local 2002.09.28
在线测试地址：POJ 2349，ZOJ 1914，UVA 10369
试题解析
简述题意：有两种不同的通信技术:卫星通信和无线电通信，卫星通信可在任两个哨所间任意联络；但采用无线电通信的哨所只能和距离不超过D的哨所联系。无线电的能力越高(即传输距离D越大)，花费就越大。已知无线电数目m，计算最小的D使得每对哨所之间至少有一条(直接或间接的)通信路径。
我们将哨所作为节点，把所有可以互相通信的哨所连接起来，边权设为相连的两个哨所的距离，则可构造出一个完全无向图。要在这个完全无向图中划分出S个连通分支，每个连通分支内节点间的边权不大于D，即位于同一连通分支内的哨所间采用无线电收发机通信，每个连通分支分配一台卫星设备，用于不同连通分支间的通信。显然卫星设备的台数就是图的连通分支数，目标是求连通分支内边长的上限D(即最小收发距离)。解题有两种策略：
1) 正向思考：在已知连通分支数S的基础上求连通分支内边长的上限D。
2) 逆向思维：在已知连通分支内边长上限D的基础上求连通分支数S。
显然，正向思考的策略似乎难以施展，因为P个哨所可构成由P*(P-1)2」条边组成的完全图。要在这张图中找到连通分支内边长上限D，使得删去大于D的边后连通分支数正好为S是相当困难的。而逆向思维的策略相对简单，在正向思考受阻的情况下，应该“正难则反”，逆向考虑问题。于是问题转化为：找到一个最小的D，使得把所有权值大于D的边去掉之后，连通分支数小于等于S。由此引出一个定理：
【定理1.2-1】　如果去掉所有权值大于D的边后，最小生成树被分割成为S个连通分支，图也被分割成为S个连通分支。
证明：用反证法。假设最小生成树被分割成为S个连通支，原图被分割成S′(S′≠S)个连通支，由于最小生成树是原图的一个子图，因此S′有了这个定理，很容易得到一个构造性算法：最小生成树的第S长的边就是问题的解。
证明：首先，D取最小生成树中第S长的边是可行的。如果D取第S长的边，我们将去掉最小生成树中前S-1长的边，最小生成树将被分割成为S部分。由定理1.2-1，原图也将分割成为S部分(可行性)。其次，如果D比最小生成树中第S长的边小的话，最小生成树至少被分割成为S+1部分，原图也至少被分割成为S+1部分。与题意不符(最优性)。
综上所述，最小生成树中第S长的边是使得连通分支个数≤S的最小的D，即问题的解。(证毕)
由于通信图的节点数不多(P≤500)，对应完全图的边数不是太多，因此我们在计算最小生成树上采用了Kruskal算法。
程序清单

#include <iostream>
#include <cstring> 
#include <cstdio> 
#include <cmath> 
#include <algorithm> 
using namespace std ; 
 
const int MAXN = 505 ; 
 
struct　Edge　　　　　　　　　　　　　　　// 边的结构定义
{
int　start , end ;// 边的两个端点
double length ;// 边长
bool visit ;// 最小生成树的边标志
} edge［MAXN * MAXN］ ;// 边集
 
struct　Point// 点的结构定义
{ 
int　x , y ;// 坐标
} point［MAXN］ ;// 点集
 
int　father［MAXN］,Count ;// 节点i所在连通分支的代表节点为father［i］，完全图的
// 边数为Count
 
double　getlength( Point a , Point b )// 计算a点和b点的欧氏距离
{ 
double len ; 
len=sqrt(double((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y ))) ; 
return len ; 
} 
 
bool　cmp( Edge a , Edge b )// 比较a和b的边长大小
{ 
return a.length < b.length ; 
} 
 
int　find( int x )// 计算x点所在连通支的代表节点
{ 
if( father［x］ == x ) return x ; 
father［x］ = find( father［x］ ) ; 
return father［x］　　　　　　　; 
} 
 
bool Union( int x , int y )// 合并：若x和y不在同一连通分支，则代表节点序号小的
// 连通分支并入代表节点序号大的连通分支，并返回合并标志
{
int　f1 = find( x ) ;// 计算x所在连通分支的代表节点f1
int　f2 = find( y ) ;// 计算y所在连通分支的代表节点f2
if( f1 == f2 ) return false ;// 若x和y在同一连通分支，则返回false
else if( f1<f2 )father［f1］=f2;// 合并x和y所在的连通分支，返回合并标志
else father［f2］ = f1 ; 
return true ; 
}
 
double kruskal( int n )// 使用Kruskal算法计算最小生成树
{ 
int　i , j = 0 ; 
double sum = 0 ; 
for(i=0;i< n;i ++) father［i］=i;// 初始时每个节点自成一个连通分支
sort( edge,edge+Count,cmp ) ;// Count条边按边长递增顺序排列
for(i=0;i<Count && j<n;i++)// 枚举每条边，构造n-1条边的最小生成树
{ 
if (Union(edge［i］.start,edge［i］.end))// 若第i条边的两个端点不在同一连通分支，则加入最小生成树 
{ 
sum += edge［i］.length;// 边长计入最小生成树的边权和
edge［i］.visit　= 1 ;// 第i条边为最小生成树的树边
j ++ ; 
} 
} 
return sum ;// 返回最小生成树的边权和
} 
 
int　main() 
{ 
int　T , S , P ;// 测试用例数T，卫星频道数S，哨所数P
int　i , j ; 
scanf( "%d" , & T ) ;// 输入测试用例数 
while( T -- )// 依次处理每个测试用例
{ 
Count=0 ;// 完全图的边数初始化
scanf( "%d%d",&S ,&P );// 输入卫星频道数和哨所数 
for( i=0;i<P;i++ )// 输入每个哨所的坐标
scanf( "%d%d" , & point［i］.x , & point［i］.y ) ; 
for( i=0;i<P-1;i++ )// 以哨所为节点构造完全图
for( j=i+1;j<P;j++) 
{// 记下第Count条边的端点和边长
edge［Count］.start=i;edge［Count］.end=j; 
edge［Count］.length=getlength( point［i］ , point［j］ ) ; 
edge［Count］.visit=0 ;// 设置非生成树边标志
Count ++ ;// 完全图的边数+1
} 
kruskal( P ) ;// 构造完全图的最小生成树
for( i=Count-1;i>= 0;i-- ){// 按照边长递减顺序枚举最小生成树的S条树边，第S大的树边
// 即为连接网络的最小D值
if( edge［i］.visit ) 
{ 
S -- ; 
if( S == 0 ) break ; 
} 
} 
printf( "%.2f＼n",edge［i］.length );// 输出连接网络的最小D值
 } 
return 0 ; 
}

一道看似毫无头绪的试题被最小生成树的算法破解了，显示出最小生成树的魅力。在解题过程中，一个对最小生成树本质特征的揭示在最小生成树和图的连通分支之间搭起了一座桥梁，正是这座桥梁引领我们顺利到达了胜利的彼岸。
在程序设计竞赛中，有些看似与最小生成树风马牛不相干的几何计算题，也可以经过分析转化为图论模型，并采用最小生成树去解决。我们不妨来看下面两个范例。
【1.2.2　Robot】
【问题描述】
在不久的将来，机器人要给参加巴尔干半岛奥林匹克信息学竞赛(Balkan Olympiad in Informatics)的选手运送食品。机器人将所有的食品放置在一个单一的方形托盘中。不幸的是，在厨房和选手厅之间的路径上充满了各种障碍，因此，机器人不能带任意大小的托盘。请你编写一个程序zad1.exe，确定可用于餐饮的最大可能的托盘的尺寸。
机器人要行走的路径是平行墙壁包夹的走廊，走廊只能有90°转角。走廊在X轴正方向开始。障碍是一些立柱，被表示为点，它们都是在包夹走廊的墙壁之间。为了使机器人能够走过这段路径，托盘不能撞到立柱或墙壁——它可能只是边与边“触摸”。机器人和它的托盘只能在X或Y轴方向上转换移动。　假定机器人的尺寸小于托盘的尺寸，机器人完全在托盘之下(见图1.2-4)。

输入：
在文件ZAD1.DAT的第一行是一个整数m(1≤m≤30)，表示直线墙的线段的数量。接下来的m+1行是所有转弯点(包括端点)的“上部分”墙体的x和y坐标，相似地，接下来的m+1行是所有转弯点(包括端点)的“下部分”墙体的x和y坐标。然后的一行给出整数n(0≤n≤100)，表示障碍物的数量，接下来n行是障碍物的x和y坐标。所有坐标是绝对值小于32001的整数。
输出：

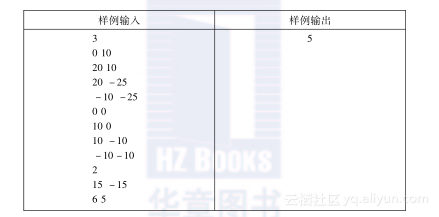
试题来源：Balkan Olympiad in Informatics 2002
在线测试地址：HDOJ 4840
试题解析
简述题意：m条含上下部分的直线墙互相连接、以90°转角组成一条走廊，走廊墙壁之间有部分障碍物。机器人举托盘沿走廊行走，托盘不能撞到障碍物或墙壁。问托盘的边长最大为多少时机器人才能走过走廊。
设li为穿行第i条走廊时盘子的最大边长。显然，机器人要顺利穿行n条走廊，则盘子的最大边长为min1≤i≤n{li}。显然问题的关键是，在已知第i条走廊的“上部”墙线段和“下部”墙线段的情况下如何计算li？下面，我们就来讨论这个问题。
解法1：通过二分+模拟的算法查找能够通过走廊的盘子的最大尺寸。
这是一种比较容易想到的方法。为了提高查找效率，我们做了如下优化。
首先，对机器人和障碍物作一个“换位”思考：
根据题意，机器人是正方形，障碍物是点(见图1.2-5a)；如果把机器人的尺寸移植到障碍物上，那么机器人就成了一个点，而障碍物就是正方形了(见图1.2-5b)。显然这两个问题是等价的。

要让一个点通不过，唯一办法就是用障碍物把走廊堵住。这里的“堵住”，就是说障碍物将在走廊的两堵墙之间形成一条通路。于是，这道题就被转化成一个图论问题：
把障碍物和墙壁看作图中的点，点p1(x1，y1)和点p2(x2，y2)之间的距离max{x1-x2，y1-y2}为边的权值，按照这一公式定义障碍点间的距离；障碍物与墙壁的距离就是障碍点与墙壁上所有点的距离的最小值；两堵墙之间的距离就是走廊的最小宽度(见图1.2-6)。

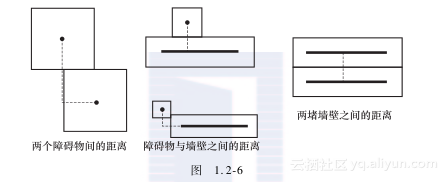
把墙壁看作起点和终点。例如图1.2-7a中的两堵墙之间有两个障碍物，在图1.2-7b中两个障碍物被分别设为顶点X和Y，两堵墙被分别设为起点U和终点V。墙与墙之间、障碍物与障碍物之间、障碍物与墙之间连边，边长为对应的距离。问题就转化为：从起点U到终点V的所有路径中最长边的最小值是多少？因为当边长达到一条路径上的最长边时，这条路径就“通”了，走廊也就被堵住了。
显然，这个问题可以在对边权进行二分计算的基础上求解，即采用“二分+宽度优先搜索”的方法解决，时间复杂度是O(n2*log2(边权上限))。这个算法效率并不理想，还有没有其他更好的算法呢？有的。
解法2：通过计算图的最小生成树得出问题的解。
先求出这个图的最小生成树，那么从起点到终点的路径就是我们所要找的路径，这条路径上的最长边就是问题的答案。这样，时间复杂度就降为O(n2)了。
可是怎么证明其正确性呢？用反证法。
证明：设起点为u，终点为v，最小生成树上从u到v的路径为旧路径，旧路径上的最长边为m。假设从u到v存在一条新路径且上面的最长边短于m。
如果新路径包含m，则新路径上的最长边不可能短于m。与假设不符。
如果新路径不包含m，则新路径一定“跨”过m。如图1.2-8，x→…→a1→a2→…ak→y是旧路径上的一段，x→b1→b2→…→bp→y是“跨”过去的一段。
如果把m去掉，最小生成树将被分割成两棵子树，显然x和y分属于不同的子树(否则最小生成树包含一个环)。因此在x→b1→b2→…→bp→y上，一定存在一条边m′，它的端点分属于不同的子树。因为最小生成树中只有m的端点分属于不同的子树，所以m′不属于最小生成树。因此m′和m一样是连接两棵子树的边。因为新路径的最长边短于m且m′属于新路径，所以w(m′)

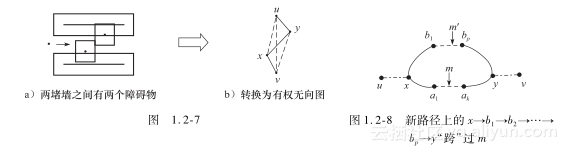
综上所述，不可能存在另一条从u到v的路径，使得它的最长边短于m。最小生成树上从u到v的路径就是最长边最短的路径，该路径上的最长边就是问题的解。(证毕)
由于图的节点数较少(≤100)，因此，采用Prim算法计算最小生成树为宜。
程序清单

#include <cstdio>
#include <cstring>
#include <cmath>
#include <iostream>
using namespace std ;
typedef struct {　　　　　　　　　　// 坐标定义
int x,y;
} pt;
 
int m,n;// 直线墙数m，障碍物数n
pt up［32］,dn［32］;// 第i个转弯点的“上部分”墙体坐标up［i］、
// “下部分”墙体坐标dn［i］
pt pr［128］;// 障碍物坐标
 
int min(int a,int b){// 计算和返回整数a、b的较小者
if (a<b) { return a; } else { return b; }
}
 
int max(int a,int b){// 计算和返回整数a、b的较大者
if (a>b) { return a; } else { return b; }
}
 
int ISIN(int a,int b,int c){// 返回区间［b,c］含a的标志
if ((a>=b) && (a<=c)) { return 1; } else { return 0; }
}
 
int gr［128］［128］;// 连通图的相邻矩阵
int wel［128］;// 节点的距离值
int inv［128］;// 节点在生成树的标志
int clc［128］;// 经过当前转弯处的障碍物标志
 
int dst(int x1,int y1,int x2,int y2,int x3,int y3){
// 当前线段(x1,y1)-(x2,y2), 障碍物(x3,y3)，计算障碍物与线段
// 在X或Y轴向上的最大距离
int d;
if (y1==y2){// 若线段是水平的,则返回max{ 线段与障碍物的垂直距离, X轴向上
// 障碍物与线段的最近距离∣障碍物的x坐标在线段的x区间外}
d =abs(y3-y1);
if (ISIN(x3,min(x1,x2),max(x1,x2))==0)
{ d=max(d, min(abs(x3-x1),abs(x3-x2)) ); }
} else {// 若线段是垂直的（x1=x2），则返回max{ 线段与障碍物的水平距离,
//  Y轴向上障碍物与线段的最近距离∣障碍物的y坐标在线段的x区间外}
d = abs(x3-x1);
if (ISIN(y3,min(y1,y2),max(y1,y2))==0)
{ d=max(d, min(abs(y3-y1),abs(y3-y2)) ); }
}
return d;
}
 
int pass(int x1,int y1,int x2,int y2,int h0,int h){
// h转弯处线段h和线段h+1的上下两部分的X区间为［x1,x2］，
// Y区间为［y1,y2］，h的奇偶标志位h0。往连通图添边
 
int i,j,v,v1;
for (i=0;i<n;i++){// 标志经过h转弯处的障碍物
if ((ISIN(pr［i］.x,x1,x2)) && (ISIN(pr［i］.y,y1,y2))){
clc［i］=1;
}　else { clc［i］=0; }
}
for (j=0;j<n;j++){// 枚举经过h转弯处的一对障碍物j和i，计算(j，i)的边权
if (clc［j］==0) { continue; }
for (i=j+1;i<n;i++){
if (clc［i］==0) { continue; }
v =max(abs(pr［i］.x-pr［j］.x),abs(pr［i］.y-pr［j］.y));
gr［i］［j］=v;
gr［j］［i］=v;
}
}
for (i=0;i<n;i++){// 枚举经过h转弯处的障碍物i，调整(n,i)和(n+1,i)的边权
if (clc［i］==0) { continue; }
v = dst( up［h］.x , up［h］.y , up［h+1］.x , up［h+1］.y , pr［i］.x , pr［i］.y );
v1 = dst( dn［h］.x , dn［h］.y , dn［h+1］.x , dn［h+1］.y , pr［i］.x , pr［i］.y );
gr［n］［i］ = min(gr［n］［i］,v);
gr［i］［n］ = min(gr［i］［n］,v);
gr［n+1］［i］ = min(gr［n+1］［i］,v1);
gr［i］［n+1］ = min(gr［i］［n+1］,v1);
}
if (h0==0) {// 若h为偶数，则调整（n,n+1）的边权
v = y2-y1;
} else{ v=x2-x1; }
gr［n］［n+1］ = min(v,gr［n］［n+1］);
gr［n+1］［n］ = min(v,gr［n+1］［n］);
return 0;
}
 
int deik(void){// 使用Prim算法计算连通图gr［］［］的最小生成树
int c,i,v,v1;
c = n+2;// 计算最小生成树的节点数
for (i=0;i<c;i++){// 所有节点在生成树外，距离值为∞
wel［i］=0x7FFF;
inv［i］=0;
}
wel［c-2］ = 0;// 节点n为根，其距离值为0
for (;;){
v1 = 0x7fff; v=-1;// 在生成树外寻找距离值最小(v1)的节点v
for (i=0;i<c;i++)
if (inv［i］==0)
if (wel［i］<v1) { v1=wel［i］; v=i; }
if (v<0) { break; }// 若生成树外无节点，则成功退出；否则v进入生成树
inv［v］ = 1;
for (i=0;i<c;i++)// 对生成树外节点的距离值进行松弛操作
if ((inv［i］==0) && (gr［v］［i］<0x7fff))
wel［i］ = min( max(v1,gr［v］［i］) , wel［i］ );
}
return wel［c-1］;// 返回最小生成树的最长边
}
 
int main(void){
int test;
scanf("%d",&test);// 输入测试用例数
while(test--){// 依次处理每个测试用例
int i,a,b,c,d,r;
scanf("%d ",&m);// 输入直线墙的线段数
// 输入m+1个转弯点（包括端点）的“上部分”墙体坐标和下部分”
// 墙体坐标
for (i=0;i<=m;i++) scanf("%d %d ",&up［i］.x,&up［i］.y);
for (i=0;i<=m;i++) scanf("%d %d ",&dn［i］.x,&dn［i］.y);
scanf("%d ",&n);// 输入障碍物数和每个障碍物的坐标
for (i=0;i<n;i++) scanf("%d %d ",&pr［i］.x,&pr［i］.y);
memset(gr,0x11,128*128*sizeof(int));
for (i=0;i<m;i++){// 枚举每个转弯点。计算邻接于第i个转弯点的两条线段的X轴区间
// ［a,c］、Y轴区间［b,d］，根据该信息往连通图添边
a = min( min( up［i］.x , up［i+1］.x ) , min( dn［i］.x , dn［i+1］.x ) );
b = min( min( up［i］.y , up［i+1］.y ) , min( dn［i］.y , dn［i+1］.y ) );
c = max( max( up［i］.x , up［i+1］.x ) , max( dn［i］.x , dn［i+1］.x ) );
d = max( max( up［i］.y , up［i+1］.y ) , max( dn［i］.y , dn［i+1］.y ) );
pass(a,b,c,d,i%2,i);
}
r = deik();// 使用Prim算法计算和输出连通图的最小生成树的最长边
printf("%d＼n",r);
}
return 0;
}

【1.2.3　Qin Shi Huangs National Road System】
【问题描述】
在中国古代的战国时期(公元前476年至公元前221年)，中国分成7个国家——齐、楚、燕、韩、赵、魏、秦。嬴政是秦国的国王。经历了9年的战争，嬴政终于在公元前221年征服了其他六个国家，成为统一中国的第一个皇帝。这就是秦朝——中国的第一个王朝(清朝是中国的最后一个王朝)。所以嬴政自称“秦始皇”，因为“始皇”在中文中的意思是“第一个皇帝”。
秦始皇主持了许多巨大的工程项目，其中就包括中国长城的第一个版本、著名的秦始皇兵马俑以及一个巨大的国家道路系统。下面是一个关于道路系统的故事：
在中国有n座城市，秦始皇希望用n-1条道路把这些城市全部连接起来，以便他能从首都咸阳到每一个城市。虽然秦始皇是一个暴君，但他希望所有道路的总长度最小，使道路系统不必花太多的人力。道士徐福告诉秦始皇，他可以用魔法修建一条道路，而且用魔法修建的道路不用花钱，也不用使用劳动力。但徐福只能为秦始皇修建一条魔法道路，所以秦始皇要决定在哪里修建魔法道路。秦始皇希望所有不用魔法修建的道路的总长度尽可能小，但徐福则希望魔法道路要有利于尽可能多的人——所以秦始皇决定，A/B的值(A与B的比率)必须最大，其中A是两座用魔法道路连接的城市的总人口，而B是没有用魔法修建的道路的总长度。
您能帮助秦始皇吗？
每座城市被视为一个点，一条道路被视为连接两个点的一条直线。
输入：
第一行给出一个整数t，表示t个测试用例(t≤10)。
对每个测试用例：
第一行给出一个整数n，表示有n座城市(2接下来给出n行，每行给出3个整数X、Y和P(0≤X，Y≤1000，0

本题设定，每座城市的位置是不同的。
输出：
对每个测试用例，按上述要求输出一行，给出最大比率A/B。结果精确到小数点后两位。

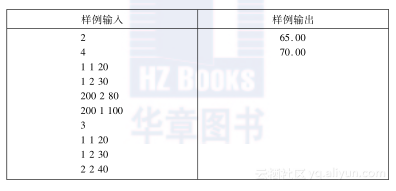
试题解析
简述题意：给出n个城市的二维坐标以及每个城市的价值(人口)，现在有人免费帮助秦始皇修理任意一条公路。如果把城市看作节点，任一对节点间连边，边权为城市间的欧氏距离，则组成了一个带权的完全无向图。按照秦始皇的旨意(连接用n-1条道路所有城市，以便他能从首都咸阳到每一个城市)，需要构建这张图的一棵生成树，使得比率A/B最大，其中A表示这条公路两端城市的价值和，B表示生成树的边权和，但不包括这条公路的长度。
显然，想要比率A/B最大，所以A要尽可能大、B要尽可能小。要使B尽可能小的话，可以先求得最小生成树T，其边权和为total。然后枚举最小生成树上的每条边(i，j)∈T，在删除该边后得到的两个点集中分别找到最大价值的节点I′和J′，两个节点的价值分别为AI′和AJ′，添加边(I′，J′)，得到的依然是一棵生成树，更新A/B比率。显然，最大比率A/B=max(i,j)∈TAI′+AJ′total-(i,j)的边长。
由于公路图为一个节点数不超过1000的完全图，因此不妨使用Prim算法计算最小生成树，并通过dfs找两个集合中的点。计算时间复杂度为O(n2)。
程序清单

#include <cstdio>
#include <cstring>
#include <iostream>
#include <cmath>
 
using namespace std;
 
const int X = 1002;　　　　　　　　　　　　// 城市数的上限
#define INF 1e12// 无穷大的定义
 
struct node// 城市的结构定义
{
int x,y,w;// 坐标(x,y)、人口w
}p［X］;// 城市序列
 
int n;// 城市数
double map［X］［X］;// 完全图的相邻矩阵
double dis［X］,total,ans;// 节点距离值dis［］，最小生成树的边权和total，最大比率
// A/B为ans
bool use［X］;// 生成树的节点标志或当前集合标志
int pre［X］;// 生成树则节点i的父指针为pre［i］
 
double dist(int x1,int y1,int x2,int y2)// (x1,y1)和(x2,y2)间的欧氏距离
{
return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
}
 
void prim()// 使用Prim算法求完全图map［］［］的最小生成树
{
memset(pre,0,sizeof(pre));// 前驱初始化
total = 0;// 最小生成树的边权和初始化
memset(use,false,sizeof(use));// 所有节点未在生成树
for(int i=1;i<=n;i++)dis［i］=INF;// 所有节点的距离值初始化
dis［1］ = 0;// 节点1为根，距离值为0
int k;
double MIN;
for(int i=0;i<n;i++)// 寻找生成树外距离值最小的节点k（距离值为MIN）
{
MIN = INF;
for(int j=1;j<=n;j++)
if(!use［j］&&dis［j］<MIN)MIN = dis［k = j］;
use［k］=true;total+=MIN;// k进入最小生成树，距离值计入边权和
for(int j=1;j<=n;j++)// 对生成树外节点的距离值进行松弛操作
if(!use［j］&&dis［j］>map［k］［j］)dis［j］=map［k］［j］,pre［j］=k; 
}
}
 
void dfs(int i)// 通过深搜i的后趋点找到所在集合use［］
{
use［i］=true;// i进入集合
for(int j=1;j<=n;j++)// 递归i后驱点中未被访问的节点
if(!use［j］&&pre［j］==i)dfs(j);
}
 
void solve()// 计算和输出最大比率A/B
{
double temp;
ans = 0;
int a,b;
for(int i=1;i<=n;i++)// 枚举每条边
{
if(pre［i］==0)continue;// 若i为根，则继续枚举
temp=total-map［i］［pre［i］］;// 删除边（i,pre［i］）
memset(use,false,sizeof(use));// 计算i所在的集合use［］
dfs(i);
a = b = 0;
for(int j=1;j<=n;j++)// 在删除边（i,pre［i］）后得到的两个点集中分别找最大价值的点
{
if(use［j］&&j!=pre［i］)// j为pre［i］所在集合的点，调整该集合最大价值
a=max(a,p［j］.w);
else if(!use［j］&&j!=i)// j为i所在集合的点，调整该集合最大价值
b=max(b,p［j］.w);
}
ans=max(ans,(a+b)/temp);// 调整ans
}
printf("%.2lf＼n",ans);// 输出最大比率A/B
}
 
int main()
{
freopen("sum.in","r",stdin);// 输入文件读准备
freopen("sum.out","w",stdout);// 输出文件写准备
int t;cin>>t;// 输入测试用例数
while(t--)
{
scanf("%d",&n);// 输入城市数
for(int i=1;i<=n;i++)// 输入每个城市的坐标和人口
{
scanf("%d%d%d",&p［i］.x,&p［i］.y,&p［i］.w);
for(int j=i;j>=1;j--)// 构造完全图的相邻矩阵map［］［］
map［i］［j］ = map［j］［i］ = dist(p［i］.x,p［i］.y,p［j］.x,p［j］.y);
}
prim();// 计算完全图的最小生成树
solve();// 计算和输出最大比率A/B
}
return 0;
}

当然，［1.2.2 Robot］和［1.2.3 Qin Shi Huangs National Road System］还有其他解法，譬如DFS搜索等。既然如此，为什么偏要选择计算最小生成树的方法呢？不仅因为它效率高、编程复杂度低，最重要的是因为它构思巧妙，颇有启发性。把两道貌似计算几何的问题转化为最小生成树模型就已经颇有新意了，再用最小生成树去解决转化后的图论问题，就更显其奥妙无穷。实际上这个思维过程是深入思考的结果。例如［1.2.2 Robot］中，我们面临的问题是如何从u到v的众多路径中选择最佳路径。如果你在u和v之间画了两条路径，并标上最长边，准备考虑如何比较它们优劣的话，会出现一个环，而且环上还有一条最长边。这时便初显出最小生成树的端倪。再如［1.2.3 Qin Shi Huangs National Road System］中，我们面临的问题是，如果删除任意一条边(i，j)，则会形成两个连通分量，在每个连通分量中各选一个价值最大的节点连边，则生成树性质保持不变，但相对(i，j)来说，A是最大的。我们按照上述思路尝试最小生成树的n-1条边，自然可得出A/B的最大比率。显然，在问题初显出最小生成树端倪的基础上，经过反复修正、严谨证明，算法会逐渐成熟起来。所以，最小生成树的应用并不是想象的那么简单，它需要敏锐的洞察力、扎实的图论基础和积极创新的思维。
1.2.2　最优比率生成树的思想和应用
前面所讲的最小生成树，指的是连通图中边权和最小的生成树，即图中每条边只有边权一个参数。
现在给出一个完全图，图中每条边设两个参数(bi和ci)，要求计算一棵生成树，使得∑(xici)∑(xibi)最小，其中xi当第i条边包含在生成树中时为1，否则为0。这样的生成树称为最优比率生成树。
最优比率生成树的计算有3种方法。
方法1：01整数规划
设xi等于1或0，表示边ei是否属于生成树。则所求比率r=∑(xici)∑(xidi)，0≤i≤n2(n-1)-1。为了使r最大，设计一个子问题：
让z=∑(dixi)-l∑(cixi)=∑(tixi)最大(其中ti=di-l*ci)，并记为z(l)，即把z(l)看做以ti为边权的最小生成树的总权值。
显然，01整数规划属于一种蛮力搜索，计算效率低。但是，我们可以从上述分析中找到z的两种性质：
【性质1.2-1】　z单调递减。
证明：因为c为正数，所以z随l的减小而增大。
【性质1.2-2】　z(max(l))=0。
证明：若z(max(l))<0，∑(dixi)-max(l)∑(ci*xi)<0，可化为1r由上面的分析，我们就将问题转化为求解比率rate使z(rate)==0，由此引出方法2和方法3。
方法2：二分法
步骤1：找出比率rate的最小值l和最大值r并设定精度范围。
步骤2：求mid=(l+r)/2。
步骤3：用di-mid*ci重新构图。
步骤4：求出新图的最小生成树权值和。
步骤5：如果权值和等于0，mid就是我们要求的比率，成功返回。如果权值和>0，l=mid；如果权值<0，rear=mid，跳回步骤2继续循环。
二分法一定能够在经过log2(r-l)次搜索之后找到所求比率。
方法3：迭代法
生成树的比率为∑生成树边ci参数∑生成树边bi参数。设：prerate为上次计算出的生成树的比率；rate为当前生成树的比率；sumc=∑生成树边ci参数；sumb=∑生成树边bi参数。
迭代过程如下：
计算连通图中每条边的参数ci和bi；

Prerat和rate初始化；
while(true)
{
用ci-rate*bi作为连通图边长重新构图G；
计算G图的最小生成树，得出生成树边的两个参数和(sumc、sumb)；
rate=sumc/sums；
if (rate-prerate≤精度要求) break;// 不可能再优化，成功退出
prerate=rate;// 记下当前生成树的比率
}
输出最优比率rate；

【1.2.4　Desert King】
【问题描述】
伟大的David刚刚成为一个沙漠国家的国王。为了赢得人民的尊敬，他决定在他的国家内建立遍布的通水渠道，实现村村通水，即和首都连通的村庄都将通水。作为国家的统治者和国家智慧的象征，他需要一个最优方式建立通水渠道。
经过几天的研究，他终于完成了他的计划。他希望通水渠道每英里的平均成本最小化。也就是说，通水渠道总成本与总长度的比例必须最小化。他只需要修建将水通到所有村庄的必要通道就可以了，这意味着，连接每个村庄到首都只有一种方式。
他的工程师调查了国家，并记录了每个村的位置。所有在两座村庄之间的通水渠道都是走直线。由于任何两个村庄的海拔高度都不同，所以工程师得出的结论是，每两个村之间的通水渠道都需要安装一个垂直传输水的升降机，可以将水向上打，或让水流下来。通水渠道的长度是两村之间的水平距离，通水渠道的成本是升降高度。您要注意每个村所在的不同的海拔高度，而且不同的通水渠道不能共享一个升降机。通水渠道能安全地相交，不会有三座村庄在同一条直线上。
作为David国王的首席科学家和程序员，请你找出建立通水渠道的最佳解决方案。
输入：
存在若干测试用例。每个测试用例开始的第一行给出整数N(2≤N≤1000)，表示村庄的数目。接下来的N行每行给出3个整数x、y和z(0≤x，y<10000，0≤z<10000000)。(x，y)是村庄的位置，z是海拔高度。第一个村庄是首都。以N=0结束输入，程序不用处理。
输出：
对于每个测试用例，输出一行，给出一个十进制数，表示通水渠道总成本与总长度的最小比值。这个数字精确到小数点后的三位。

试题解析
简述题意：已知n个村庄的坐标和海拔高度。任两个村庄之间存在高度差和欧氏距离两个数据。要求把任两个村庄直接或者间接连通，且所有连通边的高度差之和除以距离和值最小。
将村庄作为节点，任两个村庄间互通，则构成了一个完全图。通水渠道的成本取决于相邻两个村庄高度差的绝对值，长度是两村之间的水平距离。因此每条边有两个参数：两个端点高度差的绝对值bi；两个端点间的欧氏距离ci。由于需要实现村村通水且通水渠道的总成本与总长度的比例必须最小化，因此可看出此题就是一个典型的最优比率生成树问题。
下面，分别给出二分法和迭代法的程序范例。由于图的节点数较少(≤1000)，因此采用Prim算法计算最小生成树。
程序清单

方法1：二分法#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
#define MAX 1001　　　　　　　　　　　　　　　// 节点数的上限
#define INF 1000000000// 定义无穷大
struct node// 节点的结构定义
{
double x,y,h;// 坐标和高度
}dot［MAX］;// 节点序列
 
inline double dis(double x1,double y1,double x2,double y2)
// （x1,y1）至(x2,y2)的欧氏距离
{
return sqrt( (x2-x1)*(x2-x1)+(y2-y1)*(y2-y1) );
}
double graph［MAX］［MAX］;// 相邻矩阵
inline void creat(int n,double l)// 构造新图的相邻矩阵graph［］［］
{
int i,j;
for(i=1;i<=n;i++)
{
for(j=1;j<=n;j++)
{
graph［i］［j］=fabs(dot［i］.h-dot［j］.h)-l*dis(dot［i］.x,dot［i］.y,dot［j］.x,dot［j］.y);
}
}
}
inline double prim(double graph［MAX］［MAX］,int n)
// 使用Prim算法构造连通图graph［］［］的最小生成树
{
bool visit［MAX］={0};// 所有节点在生成树外
int mark;// 进入生成树的节点序号
double dis［MAX］;// 节点的距离值
double ans=0;// 最小生成树的边权和初始化
int i,j;
visit［1］=true;// 以节点1为根，计算各节点的距离值
for(i=1;i<=n;i++)
dis［i］=graph［1］［i］;
for(i=1;i<n;i++)// 逐条边加入生成树
{
int minnum=INF;// 在生成树外的节点中寻找距离值最小的节点mark，
// 其距离值为minnum
for(j=1;j<=n;j++)
{
if(!visit［j］&&dis［j］<=minnum)
{
minnum=dis［j］;
mark=j;
}
}
visit［mark］=true;　ans+=dis［mark］;
// mark进入生成树，距离值计入边权和
for(j=1;j<=n;j++)// 对生成树外节点的距离值进行松弛操作
{
if(!visit［j］&&graph［mark］［j］<dis［j］)
dis［j］=graph［mark］［j］;
}
 
}
return ans;// 返回最小生成树的边权和
}
 
int main()
{
int i,j;
int n;// 节点数
double res;// 当前生成树的边权和
while(scanf("%d",&n))// 反复输入节点数，直至输入0为止
{
if(n==0)
break;
for(i=1;i<=n;i++)// 输入每个节点的坐标和高度
{
scanf("%lf%lf%lf",&dot［i］.x,&dot［i］.y,&dot［i］.h);
}
double front,rear;　front=0;　rear=100;
// 通水渠道总成本/总长度的比值区间初始化
double mid;// 区间中间指针
double pre=0.0;
while(front<=rear)// 若未找到最小比值，则循环
{
mid=(front+rear)/2;// 计算中间指针
creat(n,mid);// 构造新图的相邻矩阵graph［］［］
res=prim(graph,n);// 计算新图的最小生成树的边权和
if(fabs(res-pre)<=0.0005)// 若边权和为0，则退出
break;
else if(res>0.0005)// 若边权和>0，则在右区间寻找；否则在左区间寻找
front=mid;
else
rear=mid;
}
printf("%.3lf＼n",mid);// 输出通水渠道总成本/总长度的最小比
}
return 0;
}方法2：迭代法#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
#define MAX 1001// 节点数的上限
#define INF 1000000000// 无穷大
struct node// 节点的结构定义
{
double x,y,h;// 位置（x,y），高度h
}dot［MAX］;// 节点序列
 
inline double dis(double x1,double y1,double x2,double y2)
// 计算线段(x1,y1)-(x2,y2)的欧氏距离
{
return sqrt( (x2-x1)*(x2-x1)+(y2-y1)*(y2-y1) );
}
 
 
double graph［MAX］［MAX］;// 图的相邻矩阵
double c［MAX］［MAX］;// 存储节点间高度差的绝对值
double s［MAX］［MAX］;// 存储节点间的欧氏距离
 
inline void creatcs(int n)// 计算每对村庄间的距离和海拔高度差的绝对值
{
int i,j;
for(i=1;i<=n;i++)　　 
{
for(j=1;j<=n;j++)
{
c［i］［j］=fabs(dot［i］.h-dot［j］.h);
s［i］［j］=dis(dot［i］.x,dot［i］.y,dot［j］.x,dot［j］.y);
}
}
}
 
inline void creat(int n,double l)// 用c［i］［j］-l*s［i］［j］重新构图
{
int i,j;
for(i=1;i<=n;i++)
{
for(j=1;j<=n;j++){ graph［i］［j］=c［i］［j］-l*s［i］［j］;}
}
}
 
double sumc;// 最小生成树边长1（两端点高度差的绝对值）的和
double sums;// 最小生成树边长2（两端点的欧氏距离）的和
 
inline void prim(double graph［MAX］［MAX］,int n)// 使用Prim算法计算图的最小生成树
{
sumc=0;sums=0;// 最小生成树边长1的和与边长2的和初始化
bool visit［MAX］={0};// 初始时所有节点在生成树外
int mark;// 生成树外节点中距离值最小的节点
int pre［MAX］;// 节点父指针
double dis［MAX］;// 节点距离值（与生成树节点的最短边长）
int i,j;
visit［1］=true;// 节点1进入生成树，计算所有节点的距离值和父指针
for(i=1;i<=n;i++){ dis［i］=graph［1］［i］;pre［i］=1;}
for(i=1;i<n;i++)// 逐条边添入生成树
{
int minnum=INF;// 计算生成树外节点中距离值最小（minnum）的节点mark
for(j=1;j<=n;j++)
{
if(!visit［j］&&dis［j］<=minnum){ minnum=dis［j］;mark=j;}
}
visit［mark］=true;// 节点mark进入生成树，与生成树相连边的高度差的绝对值
// 计入sumc，欧氏距离计入sums
sumc+=c［pre［mark］］［mark］;sums+=s［pre［mark］］［mark］;
for(j=1;j<=n;j++)// 调整生成树外与mark相邻节点的距离值
{
if(!visit［j］&&graph［mark］［j］<dis［j］){dis［j］=graph［mark］［j］;pre［j］=mark;}
}
}
}
 
int main()
{
int i,j;
int n;// 村庄数
while(scanf("%d",&n))// 反复输入村庄数，直至输入0
{
if(n==0) break;
for(i=1;i<=n;i++)// 输入每个村庄的位置和海拔高度
{ scanf("%lf%lf%lf",&dot［i］.x,&dot［i］.y,&dot［i］.h); }
creatcs(n);// 计算每对村庄间的距离和海拔高度差的绝对值
double prerate=30.0;double rate=30.0;// 比率的最小值和最大值初始化
while(true)
{
creat(n,rate);// 用c［i］［j］-rate*s［i］［j］重新构图graph［］［］
prim(graph,n);// 计算图的最小生成树
rate=sumc/sums;// 计算当前生成树的比率
if(fabs(rate-prerate)<0.001)break;// 若比率相同于上次生成树的比率，则成功退出
prerate=rate;// 记下当前生成树的比率
}
printf("%.3lf＼n",rate);// 输出通水渠道总成本与总长度的最小比值
}
return 0;
}

1.2.3　最小k度限制生成树的思想和应用
对于一个加权的无向图，存在一些满足下面性质的生成树：某个特殊节点的度为一个指定数值。最小度限制生成树就是满足此性质且权值和最小的一棵生成树。把它抽象成数学模型就是：
设G=(V，E，ω)是连通的有权无向图，v0∈V是特别指定的一个节点，k为给定的一个正整数。如果T是G的一棵生成树且dT(v0)=k，则称T为G的k度限制生成树。G中权值和最小的k度限制生成树称为G的最小k度生成树。
显然，最小k度生成树问题是有实际应用价值的，因为现实生活中许多问题可以归结为该问题。下面，我们来探讨求解方法。
约定：T为图G的一棵生成树，a和b为图G的两个边子集，aE，bE。在Ｔ中增加边集a、去除边集b后得到图T+a-b，记作(+a，-b)。如果T+a-b仍然是一棵生成树，则称(+a，-b)是T的一个可行交换。
【引理1.2-1】　设T′、T是图G的两棵不同的生成树，

E(T′)＼E(T)={a1，a2，…，an}
E(T)＼E(T′)={b1，b2，…，bn}

则存在E(T)＼E(T′)的一个按照权值递增排序的边序列b′1，b′2，…，b′n，使得T+ai-b′i(1≤i≤n)仍然是G的生成树。
【定理1.2-2】　设T是G的k度限制生成树，则T是G的最小k度限制生成树当且仅当下面三个条件同时成立：
1) 对于G中任何两条与v0关联的边所产生的T的可行交换都是不可改进的。
2) 对于G中任何两条与v0不关联的边所产生的T的可行交换都是不可改进的。
3) 对于T的任何两个可行交换(+a1，-b1)和(+a2，-b2)，若a1、b2与v0关联，b1、a2不与v0关联，则有ω(b1)+ω(b2)≤ω(a1)+ω(a2)。
证明：我们从必要性和充分性这两个方面给予证明：
必要性：设T是最小k度限制生成树，则条件1）、2）显然成立。以下证明条件3）：由条件1）、2）可知，如果(+a1，-b2)和(+a2，-b1)都是T的可行交换，则有ω(b2)≤ω(a1)，ω(b1)≤ω(a2)，故ω(b1)+ω(b2)≤ω(a1)+ω(a2)；否则，或者(+a1，-b2)或者(+a2，-b1)不是T的可行交换，根据引理1，T′=T+{a1，a2}-{b1，b2}仍然是T的k度限制生成树，则ω(T)≤ω(T′)，故ω(b1)+ω(b2)≤ω(a1)+ω(a2)。
充分性：设T是k度限制生成树且满足1）、2）、3），假如有另一个k度限制生成树T′，ω(T′)<ω(T)，设

E(T′)＼E(T)={a1，a2，…，an}
E(T)＼E(T′)={b1，b2，…，bn}

显然有∑ω(ai)<∑ω(bi)，根据引理1.2-1，存在一个排列b′1，b′2，…，b′n，满足T+ai-b′i仍然是G的生成树。由ω(T′)<ω(T)得∑(ω(b′i)－ω(ai))>0，因而，在T的这n个可行交换中，一定存在某个可以改进的交换(+ai，-b′i)。由于T满足1）、2），则ai、b′i若同时与v0关联或不关联都是不可改进的。也就是说，ai和b′i中必定恰好有一个不与v0关联。不妨设ai与v0无关联，因为D′T(v0)也等于k，所以必存在另一个交换(+aj，-b′j)，满足aj与v0关联，b′j与v0无关联，且(ω(b′i)-ω(ai))+(ω(b′j)-ω(aj))>0，此与3）矛盾。因此，T′是不存在的，即T是G的最小k度限制生成树。(证毕)
由定理1.2-2，可引出定理1.2-3：
【定理1.2-3】　设T是G的最小k度限制生成树，E0是G中与v0有关联的边的集合，E1=E0＼E(T)，E2=E(T)＼E0，A={(+a，-b)a∈E1，b∈E2}，设ω(a′)-ω(b′)=min{ω(a)-ω(b)(+a，-b)∈A}，则T+a′-b′是G的一个最小k+1度限制生成树。
那么，如何求最小k度限制生成树呢？首先考虑边界情况。先求出问题有解时k的最小值：把v0点从图中删去后中可能会出现m个连通分量，而这m个连通分量必须通过v0来连接(见图1.2-9)。所以，在图G的所有生成树中dT(v0)≥m。也就是说，当k

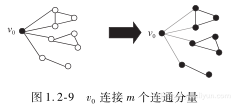
根据上述定理1.2-3，得出求最小k度限制生成树的算法框架：
步骤1：先求出最小m度限制生成树。
步骤2：由最小m度限制生成树得到最小m+1度限制生成树。
步骤3：若dT(v0)=k时停止；否则返回步骤2。
下面分别考虑每一步:首先将v0和与之关联的边分别从图中删去，此时的图可能不再连通，对各个连通分量，分别求最小生成树。接着，对于每个连通分量V′，求一点v1(v1∈V′)，且ω(v0，v1)=min{ω(v0，v′)v′∈V′}，则该连通分量通过边(v1，v0)与v0相连(见图1.2-10)。于是，我们就得到了一个m度限制生成树，不难证明，这就是最小m度限制生成树。步骤1的时间复杂度为O(Vlog2V+E)。

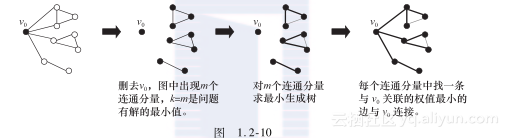
我们所求的树是无根树，为了解题的简便，把该树转化成以v0为根的有根树。假设已经得到了最小p度限制生成树，如何求最小p+1度限制生成树呢？
根据定理1.2-3，最小p+1度限制生成树肯定是由最小p度限制生成树经过一次可行交换(+a1，-b1)得到的。我们自然就有了一个最基本的想法——枚举!但是简单的枚举，时间复杂度高达O(E2)，显然是不可取的。深入思考不难发现，任意可行的交换，必定是一条边跟v0关联，另一条与v0无关，所以，只要先枚举与v0关联的边，再枚举另一条边，然后判断该交换是否可行，最后在所有可行交换中取最优值即可。于是时间复杂度降到了O(VE)，但这仍然不能令人满意。进一步分析，在原先的树中加入一条与v0相关联的边后，必定形成一个环。若想得到一棵p+1度限制生成树，需删去一条在环上的且与v0无关联的边。删去的边的权值越大，则所得到的生成树的权值和就越小。如果每添加一条边，都需要对环上的边一一枚举，时间复杂度将比较高，因为有不少边重复统计多次。例如图1.2-11a给出了一棵生成树，依次添边(v0，v4)、(v0，v3)(图1.2-11b～c)。在形成的两个环中，边(v1，v2)和(v2，v3)分别被重复统计了两次(图1.2-11d)。

此时，动态规划便有了用武之地。设Best(v)为v0至v的路径上与v0无关联且权值最大的边；father(v)为v的父节点。
状态转移方程：Best(v)=max{Best(father(v))，ω(father(v)，v)}；
边界条件：Best［v0］=-∞，Best［v′］=-∞(v0，v′)∈E(T)。
状态共V个，每次状态转移的时间复杂度为O(1)，所以时间复杂度为O(V)。故得出步骤2(由最小p度限制生成树得到最小p+1度限制生成树)的时间复杂度为O(V)。由于这一计算过程直至dT(v0)=k时为止，因此步骤2和步骤3的时间复杂度为O(kV)。
综上所述，求最小k度限制生成树算法总的时间复杂度为O(Vlog2V+E+kV)。下面，我们通过一个范例来体验最小k度限制生成树的应用和程序实现。
【1.2.5　Picnic Planning】
【问题描述】
Contortion Brothers是一群著名的马戏团小丑，众所周知，他们有着令人难以置信的能力，能把无限多的自己塞进即使是最小的车辆。在演出淡季，他们喜欢聚在当地的一个公园举行年度的柔术演员会议(Annual Contortionists Meeting，ACM)。然而，他们不仅受限于狭窄的空间，而且缺钱，所以他们尝试找一个方法使得参加会议的每个人的车的里程数最小(以节省汽油、减少磨损等)。为此，他们要把自己挤塞进尽可能少的汽车内，并且尽量使他们的所有车辆的总里程数最小化。这就导致了这样的情况，许多人开车到一个同伴的家，把他们的车放在那里，与同伴挤进一辆车中。然而，在公园也有一条约束：在野餐地点的停车场只能容纳有限数量的汽车，所以必须考虑到整体的计算。此外，由于公园的门票原因，一旦一个同伴的车到了公园，他就不能放下他的乘客，然后离开去接其他的同伴。现在请你编写一个程序来解决他们的里程数最小化问题。
输入：
输入给出一个问题的测试用例。第一行给出一个整数n，表示连接马戏团小丑之间或马戏团小丑和公园之间的公路的条数。接下来的n行每行表示一个公路连接，形式为“name1 name2 dist；”，其中name1和name2是马戏团两个小丑的名字，或者一个是小丑的名字，另一个是单词Park(顺序是任意的)；dist是一个整数，表示他们之间的距离。这些公路都是双向的道路，距离总是为正。马戏团小丑的最大数量为20，任何name最多为10个字符。接下来的最后一行给出一个整数，表示在野餐的地点可以停车的数量。本题设定从每个小丑的家到公园都有一条路径，每个测试用例都存在解。
输出：
输出一行，格式如下。Total miles driven: xxx其中xxx是总的里程数除以所有小丑的车辆数。

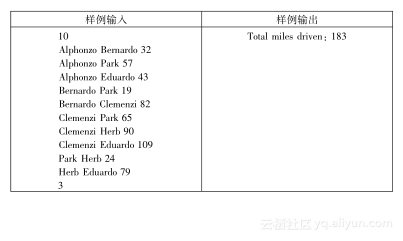
试题解析
简述题意:有一群小丑开车到公园，但公园停车场只能停k辆车。不过呢，这群小丑可以先开车到另外一个小丑家里，然后搭他的便车(车上没有人数限制)到公园。他们希望车驶过的路径长度最小，问最短距离是多少。
如果将小丑作为节点，道路作为边，则构成一个带权的无向连通图。试题要求计算一棵以节点v0(公园)为根的生成树，但这棵生成树并不是严格意义上的最小k度限制生成树，而是在v0的度不超过k情况下的最小生成树。也就是说，并不一定要求v0的度数为k，只要图的总权值不能继续减小，计算就可以结束。
我们按照如下步骤计算这棵生成树：
1) 将v0从图中删除，将得到p个连通分量。
2) 对每个连通分量求最小生成树。
3) 从每个连通分量中找出与v0关联的权值最小的边，与v0相连接，这样将得到v0的最小p度生成树。
4) 如果k

5) 如果k≥p，则考虑构建p+1度最小生成树，即加入每一条与v0相连且不在当前生成树的边。
6) 显然，在步骤5)添加一条与v0相连的树外边，必然会存在一个环，删掉该环中与v0不关联的权值最大边，将得到一棵最小生成树，且v0是p+1度的。若p+1度最小生成树的边权和大于p度最小生成树的边权和，则直接输出p度最小生成树的边权和；否则重复步骤5)、6)，直至k度最小生成树出现为止。
由于节点数较少(n≤20)，因此算法步骤1)、2)、3)可以用Prim算法实现，时间复杂度为O(n2)；在步骤5)、6)、中，若通过蛮力枚举每条边来进行增删操作的话，则时间复杂度是O(n2)，致使总复杂度达到O(kn2)。为了提高效率，我们在增删边的操作中设立了一个del［］数组，其中del［i］记录了v0→vi路径上的最长边。加入边(v0，i)、删除边del［i］便形成了一棵p+1度的最小生成树，其边权和=原边权和-del［i］的边权+(v0，i)的边权。显然，每次只要枚举max{del［i］的边权-(v0，i)的边权}，即可使得生成树的边权和最大幅度地减少。注意每次操作后都要更新该连通块的del［］，这样可将时间复杂度降为O(kn)。
程序清单

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<queue>
#include<stack>
#include<string>
#include<vector>
#include<cstdlib>
#include<map>
#include<set>
using namespace std;
#define inf 0x3f3f3f3f// 定义无穷大
const int maxn = 25;// 节点数的上限
int m,n,k,g［maxn］［maxn］,dis［maxn］,pre［maxn］,ans;
// 图的节点数n，边数m，相邻矩阵g［］［］；节点i的距离值（生成树外的节点i连接生成树内节点的最短边长）
// 为dis［i］，该节点的前驱为pre［i］；k度最小生成树的边权和为ans
bool vis［maxn］,link［maxn］［maxn］;// link［］［］数组保存在生成树中的边；生成树内节点的
// 标志vis［］
struct node// 边节点的结构定义
{
int u,v,len;// 边(u，v)的权为len
node(){}
node(int u, int v, int len):u(u),v(v),len(len){}
}del［maxn］;// del［i］保存节点0到节点i的路径上的最长边
int kk;
 
void prim(int st)// 使用Prim算法求包含st的连通块的生成树
{
vis［st］ = 1;// st进入生成树
memset(pre, -1, sizeof(pre));// 所有节点的前驱指针初始化为空
for (int i = 1; i < n; ++i)// 定义所有节点的距离值和前驱指针
{ dis［i］ = g［st］［i］; pre［i］ = st; }
while(1)
{
int tmp = inf, nt = st;// 在树外节点中找出距离值最小的节点nt
for (int i = 1; i < n; ++i)
{
if (!vis［i］ && dis［i］ < tmp) { nt = i; tmp = dis［i］; }
}
if (st == nt) break;// 该连通分量的最小生成树已形成
if(g［0］［nt］<g［0］［kk］)kk=nt;// kk保存该连通分量到节点0距离最近的点
link［pre［nt］］［nt］ = link［nt］［pre［nt］］=1;
// 将边加入生成树中
vis［nt］=1; ans+=dis［nt］;// nt为生成树内的节点，其距离值累计入生成树的总权和
for (int i=1; i<n; ++i)// 调整生成树外每个节点的前驱和距离值
{
if(!vis［i］&&dis［i］>g［nt］［i］)// 若i在树外且(nt,i)的边长小于i的距离值，则调整i
// 的前驱和距离值
{ pre［i］ = nt; dis［i］ = g［nt］［i］; }
}
}
}
 
void dfs(int cur,int cpre,int u,int v)// 修改当前连通分量中到达节点0的路径上的最大边。
// cur为当前节点，cpre为当前节点的前驱，(u,v)表示
// 调整前路径上的最大边
{
for (int i = 1; i < n; ++i)// 枚举树中除(cpre,cur)外与cur相连的每条边
{
if (cpre != i && link［cur］［i］)
{
if(cpre==-1||g［cur］［i］>=g［u］［v］)
// 若当前边权大于之前保存的最大边，则当前边记为最大
// 边，继续递归；否则最大边不变，继续递归
{ del［i］=node(cur, i, g［cur］［i］); dfs(i, cur, cur, i); }
else { del［i］ = node(u, v, g［u］［v］); dfs(i, cur, u, v); }
}
}
}
 
void solve()// 计算和输出k 度最小生成树的边权和
{
for (int i = 1; i < n; ++i)// 枚举节点0外不在生成树的每个节点i
{
if (vis［i］) continue;
k--; kk = i;// 计算剩余的度数，记下i
prim(i);// 计算以i为根的最小生成树
ans+=g［0］［kk］;link［kk］［0］=link［0］［kk］=1;
// (i,0)加入生成树，累计边权
dfs(kk, -1, -1, -1);// 调整当前连通分量的最长边
}
while(k--)
{
int c = 0, nt = 0;
for (int j = 1; j < n; ++j)// 枚举生成树外邻接节点0的所有节点
{
if (link［0］［j］ || g［0］［j］ == inf) continue;
if(c < del［j］.len - g［0］［j］)// 找出使得边权和减少量最大的添删操作，即添边（0,nt），
// 删除节点0到节点nt的路径上的最长边后使得边权和
// 减少量最大
{ nt=j; c=del［j］.len-g［0］［j］;// 记下边权和的减少量
}
}
if (c == 0) break;// 若生成树的边权和无法减少，则退出循环
ans -= c;// 调整生成树的边权和
link［del［nt］.u］［del［nt］.v］=link［del［nt］.v］［del［nt］.u］=false;
// 删除最长边
link［0］［nt］ = link［nt］［0］ = 1;// 添加边（0,nt）
dfs(nt, 0, -1, -1);// 调整当前连通分量的最长边
}
printf("Total miles driven: %d＼n",ans);// 输出k 度最小生成树的边权和
}
 
void init()// 输入边信息，构造图的相邻矩阵
{
char s1［20］,s2［20］;
int w, u, v;
n = 0;// 节点数初始化
map <string,int> name;
map <string,int>::iterator it1,it2;
name.clear();
name［"Park"］ = n++;// 根节点定义为0
memset(g, 0x3f, sizeof(g));// 图的相邻矩阵初始化为空
memset(vis,0,sizeof(vis));// 初始时所有节点在生成树外，生成树的相邻矩阵为空
memset(link,0,sizeof(link));
for (int i = 0; i < m; ++i)
{
scanf("%s %s %d", &s1, &s2, &w);// 输入边信息
it1 = name.find(s1); it2 = name.find(s2);
if (it1 != name.end()) u = it1->second;
// 定义两个端点的节点编号
else { name［s1］ = n; u = n++; }
if (it2 != name.end()) v = it2->second;
else { name［s2］ = n; v = n++; }
if (g［u］［v］ > w) g［u］［v］ = g［v］［u］ = w;
// 往相邻矩阵添边
}
scanf("%d", &k);// 输入度的限制数
ans = 0;// k 度最小生成树的边权和初始化
}
 
int main()
{
while(scanf("%d", &m) != EOF)// 反复输入边数
{
init();// 输入边信息，构造图的相邻矩阵
solve();// 计算和输出k 度最小生成树的边权和
}
return 0;
}

1.2.4　次小生成树的思想和应用
设G=(V，E，w)是连通的无向图，T是图G的一棵最小生成树。如果有另一棵树T1，满足不存在树T′，ω(T′)<ω(T1)，则称T1是图G的次小生成树。
现实生活中的许多问题可以归结为次小生成树问题，使得计算次小生成树的算法有实际的应用价值。下面，我们来探讨这个算法。约定：
由T进行一次可行交换得到的新的生成树所组成的集合，称为树T的邻集，记为N(T)。
【定理1.2-4】　设T是图G的最小生成树，如果T1满足ω(T1)=min{ω(T′)T′∈N(T)}，则T1是G的次小生成树。
证明：如果T1不是G的次小生成树，那么必定存在另一棵生成树T′，T′=T使得ω(T)≤ω(T′)<ω(T1)，由T1的定义式知T不属于N(T)，则：

E(T′)＼E(T)={a1，a2，…，at}，
E(T)＼E(T′)={b1，b2，…，bt}，其中t≥2。

根据引理1.2-1知，存在一个排列bi1，bi2，…，bit，使得T+aj-bij仍然是G的生成树，且均属于N(T)，所以ω(aj)≥ω(bij)，ω(T′)≥ω(T+aj-bij)≥ω(T1)，故矛盾。由此得出T1是图G的次小生成树。
通过定理1.2-4，我们就有了解决次小生成树问题的基本思路：
首先先求该图的最小生成树T，时间复杂度O(Vlog2V+E)。然后求T的邻集中权值和最小的生成树，即图G的次小生成树。问题是，如何在最小生成树T的基础上求次小生成树，这是制约算法效率的瓶颈。　

如果只是简单的枚举，复杂度很高：首先枚举两条边的复杂度是O(VE)，再判断该交换是否可行的复杂度是O(V)，则总的时间复杂度是O(V2E)。这样的算法显得很盲目。
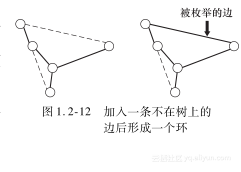
经过简单的分析不难发现，每加入一条不在树上的边，总能形成一个环(见图1.2-12)。
只有删去环上的一条边，才能保证交换后仍然是生成树，而删去边的权值越大，新得到的生成树的权值和越小。我们可以以此将复杂度降为O(VE)。这已经前进了一大步，但仍不够好。
回顾上一个模型——最小度限制生成树，我们也曾面临过类似的问题，并且最终采用动态规划的方法避免了重复计算，使得复杂度大大降低。对于次小生成树，我们也可以采用类似的思想：
1) 求图G的最小生成树T(时间复杂度为O(Vlog2V+E))；
2) 做一步预处理，通过简单的宽度优先搜索求出树上每两个节点之间的路径上的权值最大的边(时间复杂度为O(V2))；
3) 枚举图中不在树上的边(时间复杂度为O(E))。有了刚才的预处理，我们就可以用O(1)的时间得到环上权值最大的边。
由此可见，次小生成树的时间复杂度为O(V2)。下面，我们通过一个范例来体验次小生成树的应用。
【1.2.6　次小生成树Tree】
【问题描述】
小C最近学了很多最小生成树的算法，Prim算法、Kurskal算法、消圈算法等。正当小C洋洋得意之时，小P来泼小C冷水了。小P让小C求出一个无向图的次小生成树，而且这个次小生成树还得是严格次小的，也就是说：如果最小生成树选择的边集是EM，严格次小生成树选择的边集是ES，那么需要满足(value(e)表示边e的权值)∑e∈EMvalue(e)<∑e∈ESvalue(e)。这下小C蒙了，他找到你，希望你帮他解决这个问题。
输入：
第一行包含两个整数N和M，表示无向图的点数与边数。接下来M行，每行3个数x、y和z表示，点x和点y之间有一条边，边的权值为z。
输出：
包含一行，仅一个数，表示严格次小生成树的边权和(数据保证必定存在严格次小生成树)。

提示：
数据中无向图无自环；50%的数据N≤2000，M≤3000；80%的数据N≤50000，M≤100000；100%的数据N≤100000，M≤300000，边权值非负且不超过10^9。
试题来源：北京2010组队赛试题
在线测试地址：BZOJ 1977　http://www.lydsy.com/JudgeOnline/problem.php？id=1977
试题解析
显然，这道试题是次小生成树定义的直译，可直接按照次小生成树的算法求解。由于该图为稀疏图(N≤100000，M≤300000)，因此最小生成树的计算采用Kruskal算法。
程序清单

#include <iostream>
#include <vector>
#include <string.h>
#include <string>
#include <stdio.h>
#include <cstdio>
#include <algorithm>
using namespace std;
 
#define REP(I, N) for (int I=0;I<int(N);I++)
#define SZ(A) int(A.size())// 定义容器大小
#define PB push_back// 在vector尾部加入一个数据
#define MP(A, B) make_pair(A, B)// 将A和B两个值视为一个单元
 
typedef long long LL;
typedef double DB;
 
typedef pair<int, int> PII;
typedef vector<PII> VII;// 最小生成树邻接表的元素类型，第一个整数为父节点
// 序号，第二个整数为通往父亲的边序号
 
template<class T> inline void checkMin(T &a, T b){if (b<a) a=b;};
// 取最小值
 
struct edge {// 边表元素的结构类型
int a , b , w ;// (a,b)的权为w
int id ;// 边序号
friend bool operator<( edge x , edge y ){return x.w<y.w;}
// 边按权值递增排序
} ;
 
const　LL INF = 1ll<<60 ;// 定义∞
const　int N = 100000 , M = 300000 ;// 定义节点数和边数的上限
 
edge　 E［M］ ;// 边表
int　　P［N］ , R［N］ ;// x节点所在并查集的代表节点为p［x］，秩为R［x］
bool　 InMst［M］ ;// 该边在生成树的标志
 
VII　　adj［N］ ;// 最小生成树的邻接表
int　　Fa［N］ , Fb［N］ , vis［N］ ;// 最小生成树中i节点的父节点为Fa［i］，父边序号为
// Fb［i］,通往根的路径序号为vis［i］
int w［M］,s［M］ ,_i ;// 边i的权w［i］，删除树边i后应添加的树外边权s［i］，
// 路径序号_i
int　　n , m , q ;// 节点数n，边数m
LL　　 mst ;// 最小生成树的边权和
 
void　 Make(int x) { P［x］ = x ; }// 建立仅含x节点的并查集
int　Find(int x){ if(P［x］!= x)P［x］=Find(P［x］);return P［x］;}
// 返回x所在并查集的代表节点
 
void　 Union(int x, int y)// 合并x和y所在的并查集
{ if (R［x］<R［y］)P［y］=x;
else { if (R［x］ == R［y］)R［y］++ ; P［x］ = y ; }
}　 
 
void　 Kruskal()// 使用Kruskal 算法计算最小生成树
{
sort(E, E+m) ;// 按照权值递增的顺序排列边
REP(i, n) Make(i) ;// 为每个节点建立并查集
REP(i, m)// 顺序枚举每条边
{
if(Find(E［i］.a)==Find(E［i］.b))continue;
// 若第i条边在同一并查集中，则继续枚举边；否则将该边
// 加入最小生成树
Union( Find(E［i］.a) , Find(E［i］.b) ) ;
InMst［E［i］.id］=true,adj［E［i］.a］.PB(MP(E［i］.b,E［i］.id)),adj［E［i］.b］.
PB( MP(E［i］.a, E［i］.id) ) ;
mst+=E［i］.w ;// 该边权计入最小生成树的边权和
}
}
 
void　 dfs(int u, int p)// 建立生成树的父子关系
{
REP(i, SZ(adj［u］))// 枚举u的除p外的其他邻接点，建立与父节点的关系
{
int v = adj［u］［i］.first ;
if (v != p) Fa［v］=u,Fb［v］=adj［u］［i］.second, dfs(v, u);
}
}
 
int　 lca(int a, int b)// 计算生成树中a和b的最近公共祖先
{
while(a!=0){ vis［a］=_i;a=Fa［a］;}// 将a至根路径上每个节点的路径序号设为_i 
vis［0］ = _i ;
while(vis［b］!= _i)b = Fa［b］;// 从b出发向上寻找第1个路径序号为_i的节点b 
return b ;// 返回最近公共祖先b
}
 
void link(int a,int b,int c)// 边权为c的树外边(a,b)，将树内连接a和b的路径上
// 边的s值设为c
{
int p=lca(a, b), t ;// 计算树中a和b的最近公共祖先p
#define Cloze(a)if(!s［a］ && c!=w［a］)s［a］=c
// 将边a的s值设为c
// 分别将树中a和b通往公共祖先p的两条路径上途径边的s值设为c
while (a!=p){ Cloze(Fb［a］);t=Fa［a］,Fa［a］=p ,a=t;}
while (b!=p){ Cloze(Fb［b］);t=Fa［b］,Fa［b］=p,b=t;}
}
 
void　 Stat()// 计算删除树内边后应添加的树外边权s［］
{
dfs(0, -1) ;// 在以节点0为根的生成树中，建立每个节点的父关系
REP(i, m)// 枚举不在生成树的每条边，将树内连接两端点的路径上
// 节点的s值设为该边权
{
if(InMst［E［i］.id］) continue ;
_i=i+1;// 通往根的路径序号为_i（用于计算边i的两端点在树内
// 的公共祖先） 
link(E［i］.a,E［i］.b,E［i］.w); 
}
}
 
int　　main()
{
scanf( "%d%d" , &n , &m ) ;// 读节点数和边数
// 读入每条边的信息,构造相邻矩阵
REP(i, m) scanf( "%d%d%d", &E［i］.a,&E［i］.b,&E［i］.w ),E［i］.a--,E［i］.b--, E［i］.id =i,
w［i］=E［i］.w ;
Kruskal() ;// 使用Kruskal算法求最小生成树
Stat() ;// 计算删除树内边后应添加的树外边权s［］
LL ans = INF ;// 次小生成树的边权和初始化
REP(i, m)// 枚举生成树的边，若删除该边并加入树外边后可使边权和
// 增量最小，则调整次小生成树的边权和
if ( InMst［i］ && s［i］ )checkMin(ans, mst-w［i］+s［i］) ;
printf( "%lld＼n" , ans );// 输出次小生成树的边权和
}

【1.2.7　ACM contest and Blackout】
【问题描述】
为了准备“全国首届ACM学校竞赛”，也为防止在竞赛期间停电，市长决定为所有的学校提供可靠的电力来源。所以，Future电站必须和一所学校(是哪一所学校并不重要)连接；此外，一些学校也必须连接好。
本题设定，如果一家学校直接连接到Future电站，或者连接到任何其他的有可靠的电力来源的学校，那么这家学校就有可靠的电力来源。本题给出在一些学校之间进行连接的成本。市长决定挑选出两个最便宜的连接方案——总的连接成本等于学校之间的连接成本的总和。请你帮助市长找到两个最便宜的连接方案。
输入：
首先在第一行中给出测试用例的个数T(1≤T≤15)。然后给出T个测试用例，每个测试用例的第一行给出两个整数，N(3≤N≤100)表示城市中学校的数目，M表示在它们之间可能的连接，用一个空格分开。接下来M行每行给出3个整数Ai、Bi、Ci，其中Ci是在学校Ai和Bi之间连接的成本(1≤Ci≤300)。学校用从1到N的整数来编号。
输出：
对每个测试用例输出一行，给出两个整数，两个最便宜的连接方案的成本，用一个空格分开。设S1是最便宜的连接方案的成本，S2是次便宜的连接方案的成本。S1=S2当且仅当有两个最便宜的连接方案；否则S1≤S2。本题设定S1和S2是存在的。

试题解析
简述题意：在n个节点(学校)、m条边(学校连接关系)组成的带权(连接成本)连通图中，计算最小生成树的边权和(最便宜的连接方案的成本)与次小生成树的边权和(次便宜的连接方案的成本)。
由于图的节点数较少(3≤N≤100)，我们使用Prim算法计算最小生成树的边权和ans1。在计算的过程中，顺便记录树中每一对节点j、k间路径上的最长边权F［j］［k］。方法是：
若当前(v，k)进入生成树，则搜索生成树内每个节点j，F［j］［k］=max{F［j］［v］，wvk}。
有了F［］［］和ans1，便可以计算次小生成树的权值和ans2：
枚举生成树外的每一条边(i，j)(1≤i，j≤n，(i，j)T)，计算加入(i，j)、删除生成树中i与j间路径上最长边后的权值和增量(wij-F［j］［k］)。显然ans2=min1≤i,j≤n,(i,j)T{ans1+wij-F［i］［j］}。
程序清单

#include<cstdio>
#include<cstring>
#define INF 1<<30　　　　　　　　　　　// 定义无穷大
int map［110］［110］,n,m;// 图的相邻矩阵map［］［］，节点数n，边数m
int vis［110］,use［110］［110］,low［110］;// 节点i的树内标志vis［i］，距离值low［i］，
// use［i］［j］=0i和j无边
1(i,j)最小生成树T
2(i,j)∈最小生成树T
int pre［110］,F［110］［110］;// 节点i的前驱pre［i］，生成树中i至j路径上的最大
// 边权为F［i］［j］
int max(int x,int y)// 求x和y的较大者
{
return x>y?x:y;
}
int prim(int s,int t)// 使用Prim算法计算以s节点为根的最小生成树
{
int ans=0;// 最小生成树的边权和初始化
memset(pre,-1,sizeof(pre));// 每个节点的父指针初始化为空
pre［s］ = -1;// s的父指针为-1
memset(F,0,sizeof(F));// 生成树中路径的最大边初始化
for(int i = 1; i <= n; i++)// 初始时所有节点在生成树外，距离值为∞
{
vis［i］ = 0;low［i］ = INF;
}
low［1］ = 0;// 节点1的距离值为0
for(int i = 1; i <= n; i++)// 逐个节点加入生成树
{
 int temp = INF,tp=-1;// 寻找生成树外距离值最小的节点tp（距离值temp）
 for(int j=1;j<=n; j++)if(!vis［j］&&temp>low［j］){ tp = j;temp=low［j］;}
if(tp==-1) continue;
int k=tp;　int v=pre［k］;
if(v!=-1)// 若k非根，则（v, k）进入生成树
 {
use［k］［v］=use［v］［k］=2; 
for(int j=1;j<=n;j++)// 搜索生成树内的每个节点j，调整F［j］［k］
if(vis［j］)F［j］［k］=max(F［j］［v］,map［v］［k］);
}
vis［k］=1; ans+=low［k］;// k进入最小生成树，距离值累计入边权和
for(int j=1;j<=n; j++)// 调整生成树外的每个节点的距离值和父指针
if(!vis［j］&&low［j］>map［k］［j］){ low［j］ = map［k］［j］;pre［j］ = k; }
}
return ans;// 返回最小生成树的权值和
}
 
int second_mst(int x)// 根据最小生成树的权值和x计算次小生成树的权值和
{
int res=x,ans=INF;// 记下最小生成树的权值和，次小生成树的权值和初始化
for(int i=1;i<=n;i++)// 搜索生成树外每条满足条件的边(i,j)（i与j间在生成树内存
// 在路径）：若加入(i,j)、删除i与j间路径上的最长边可使权值和的增量最小，则调整次小生成树的权值和
for(int j = 1; j <= n; j++)
if(use［i］［j］==1 && map［i］［j］!=INF && F［i］［j］!=INF)
{ 
if(res+map［i］［j］-F［i］［j］<ans)ans=res+map［i］［j］-F［i］［j］;
}
return ans;// 返回次小生成树的权值和
}
 
int main()
{
int t;
scanf("%d",&t);// 输入测试用例数
while(t--)
{
 scanf("%d%d",&n,&m);// 输入节点数和边数
for(int i = 0; i<=n; i++)// 相邻矩阵map初始化
for(int j = 0; j<=n; j++) map［i］［j］ = INF;
memset(use,0,sizeof(use));// 初始时所有节点间的无边
int x,y,z;
for(int i=0; i<m; i++)// 输入m条边的信息，构造相邻矩阵并设这些边在树外
{
scanf("%d%d%d",&x,&y,&z);
map［x］［y］=map［y］［x］=z;
use［x］［y］=use［y］［x］=1;
}
int ans=prim(1,n);// 使用Prim算法计算最小生成树的边权和
int ans1=second_mst(ans);// 计算次小生成树的边权和
printf("%d %d＼n",ans,ans1);// 输出最小生成树的边权和与次小生成树的边权和
}
return 0;
}

其实，最小生成树问题的拓展形式是多种多样的，并非只有最优比率生成树、次小生成树和最小度限制生成树三种。不仅仅是最小生成树，其他经典的图论模型亦是如此。这就需要我们在解决实际问题中，不能拘泥于经典模型，要因“题”制宜，适当对经典模型加以拓展，建立起符合题目本身特点的模型。当然，这并不是说经典模型已经被淘汰了，因为经典模型与模型拓展之间有着密切的孪生关系，一切拓展都建立在原模型的基础之上。这就需要我们一方面娴熟掌握各种经典模型，另一方面根据实际情况灵活运用、大胆创新。只有这样，才能在难度日益增加的程序设计竞赛中始终立于不败之地。