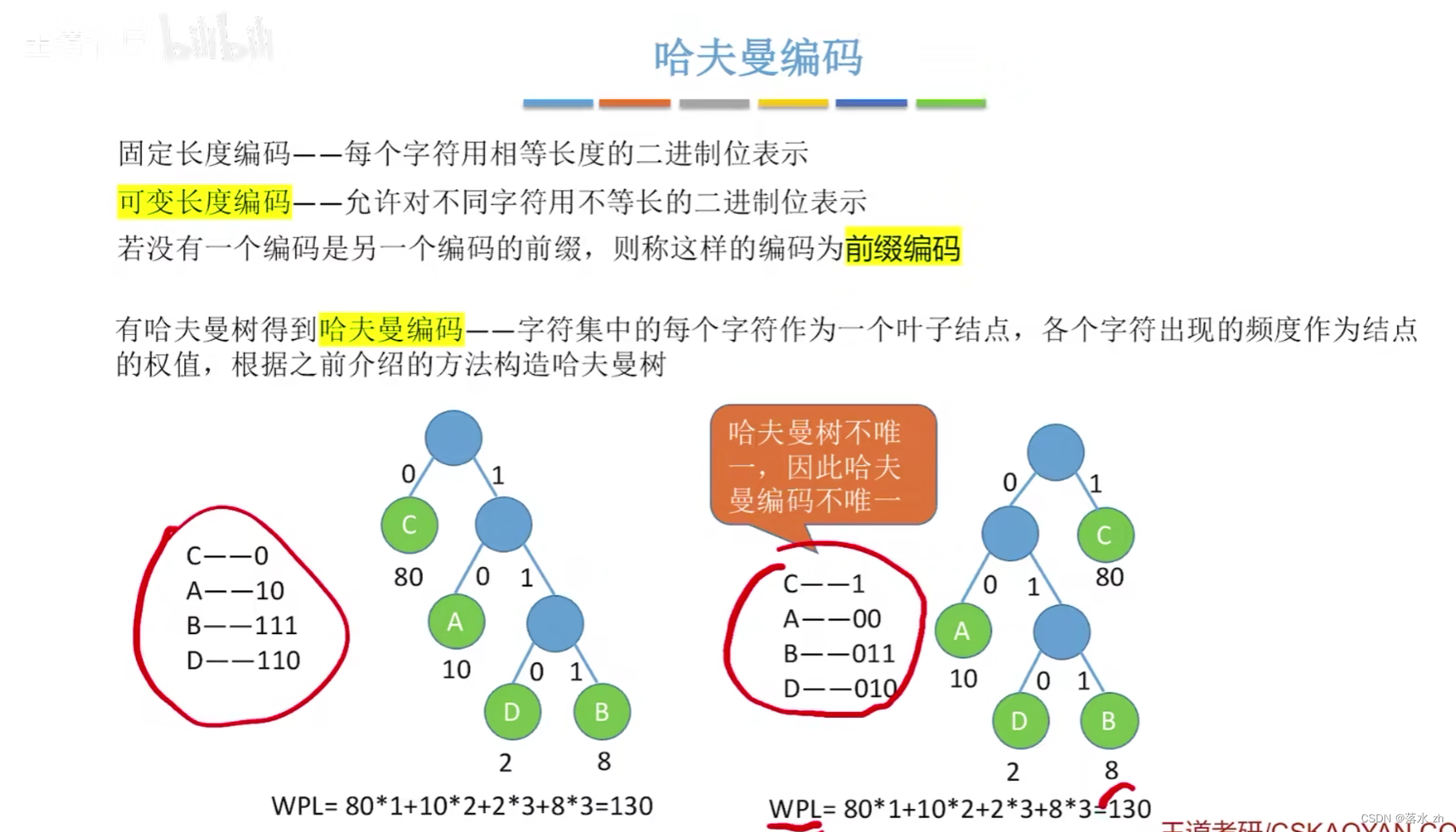
数据结构 —— 哈夫曼树_哈夫曼编码

我们今天来看哈夫曼树：

哈夫曼树

哈夫曼树（Huffman Tree），是一种特殊的二叉树，由D.A. Huffman在1952年提出，主要用于数据压缩，特别是哈夫曼编码（Huffman Coding）中。以下是关于哈夫曼树的全面概念：

定义

哈夫曼树是一种带权路径长度最短的二叉树，也称为最优二叉树。它是在给定一组具有不同权重的叶子节点（通常代表数据中的符号或字符）的情况下，通过特定的构建算法得到的。该树的特点是，所有叶子节点位于最底层或倒数第二层，且没有度为1的节点（除了根节点可能外），同时保证了从根节点到任何叶子节点的路径上的权值之和（即带权路径长度）最小。

举个例子：

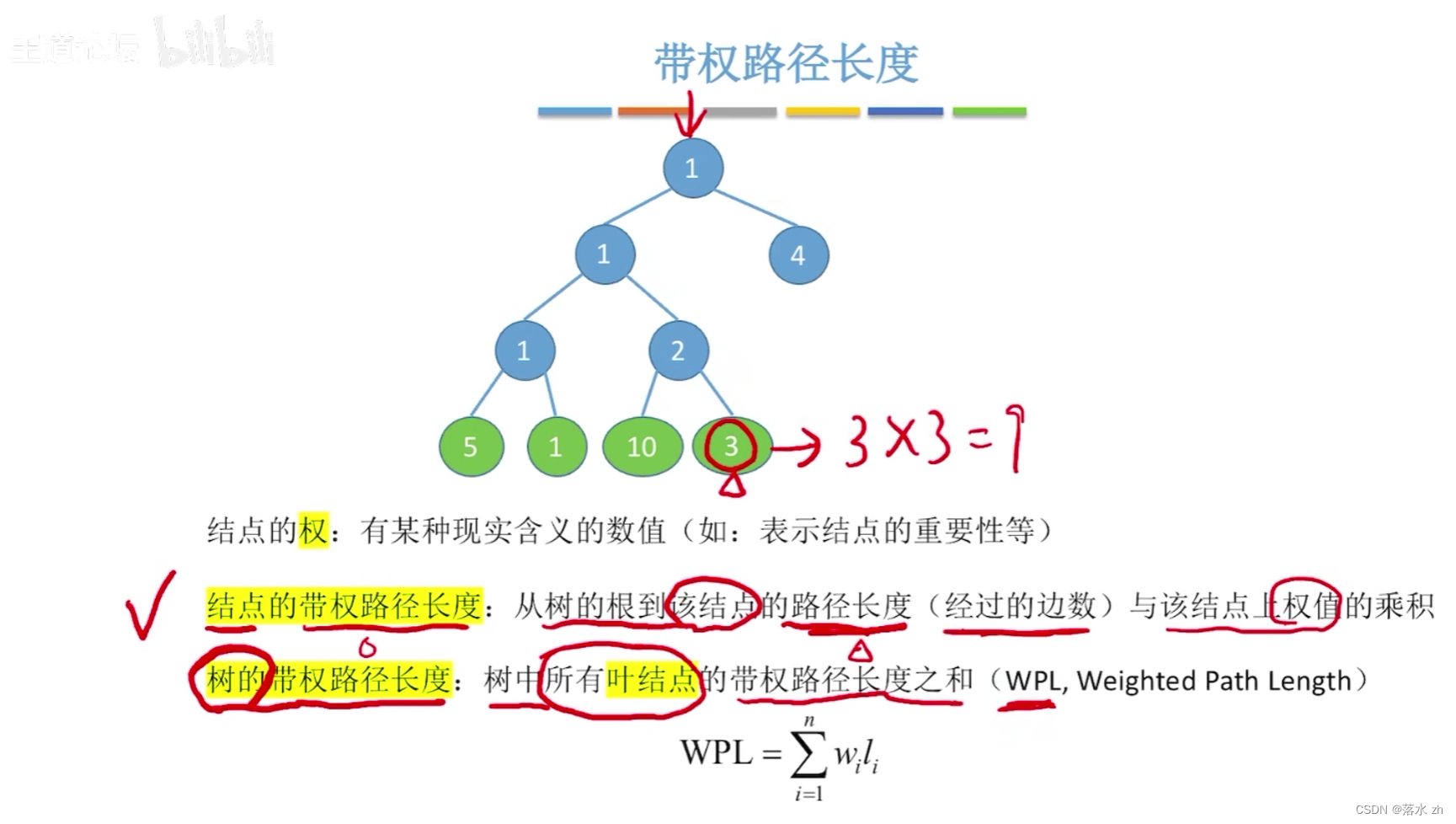
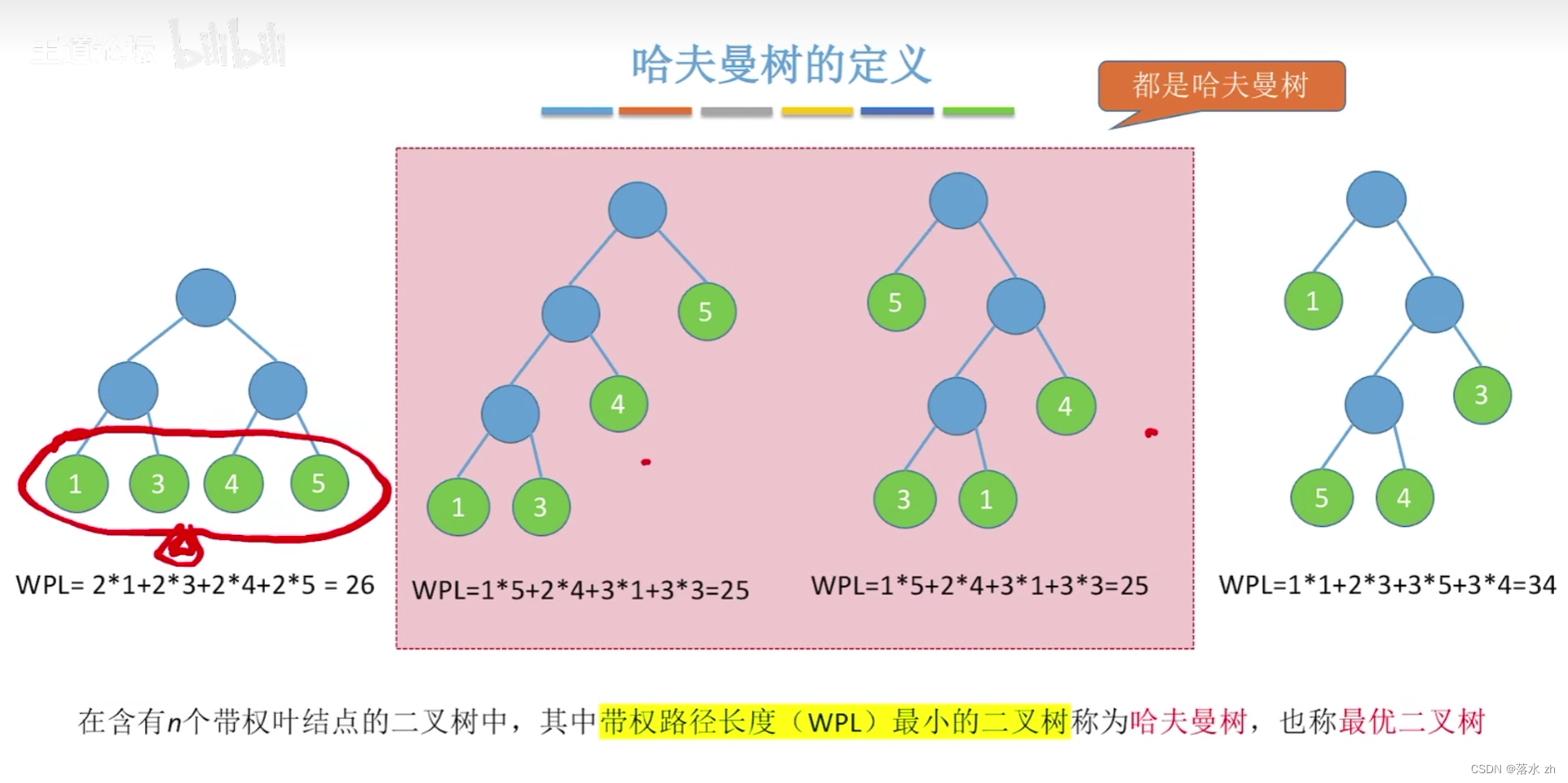
构造算法

1. 初始化：将每个权重作为一个叶子节点，放入一个优先队列（优先级基于节点权重，通常使用最小堆实现）。
2. 合并节点：从队列中取出两个权重最小的节点，创建一个新的内部节点，其权重为这两个节点的权重之和，新节点作为这两个节点的父节点。
3. 重复步骤2：将新创建的节点放回优先队列，重复上述过程，直到队列中只剩下一个节点，该节点即为哈夫曼树的根节点。
4. 生成编码：从根到每个叶子节点的路径可以转化为一个唯一的二进制字符串（路径上向左走记为0，向右走记为1），这个字符串就是该叶子节点代表的字符的哈夫曼编码。

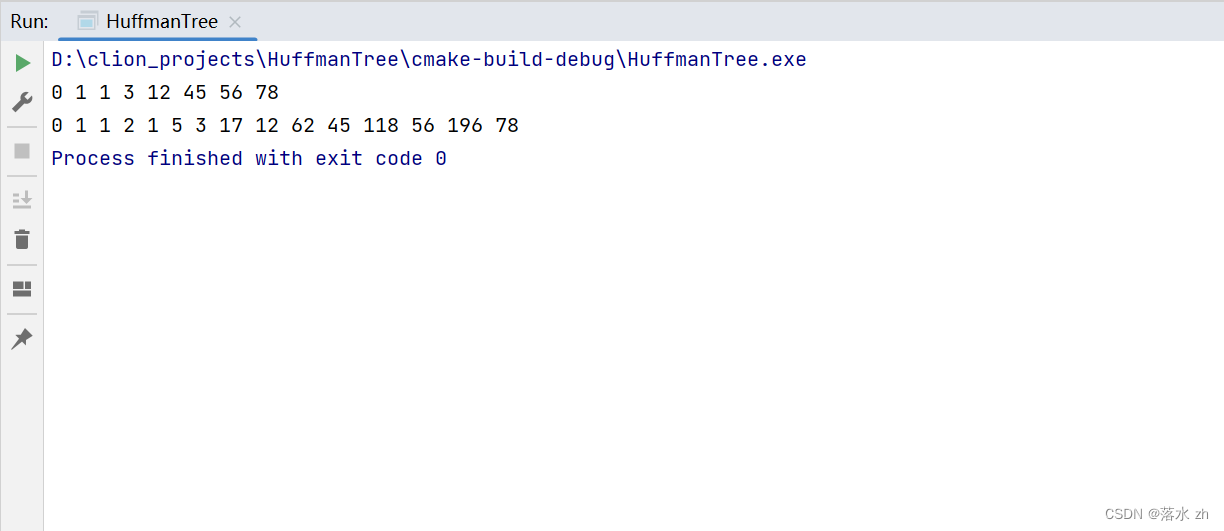
这里我没有写得那么复杂，我用一个vector维护森林，并且排好序，然后依次拿出构造哈夫曼树：

#pragma once
#include<algorithm>
#include<iostream>
#include<vector>

// 定义霍夫曼树节点结构体
template<class T>
struct HuffManTreeNode
{
public:
    // 构造函数，初始化节点数据、左孩子和右孩子
    HuffManTreeNode(T data)
            :_data(data)
            , _leftchild(nullptr)
            , _rightchild(nullptr)
    {

    }

    // 拷贝构造函数，用于复制已有节点的信息
    HuffManTreeNode(HuffManTreeNode<T>* node)
            :_data(node->_data)
            , _leftchild(node->_leftchild)
            , _rightchild(node->_rightchild)
    {

    }

    // 析构函数
    ~HuffManTreeNode()
    {

    }

    // 创建新节点并返回指针
    HuffManTreeNode<T>* CreateNode(T data)
    {
        HuffManTreeNode<T>* newnode = new HuffManTreeNode(data);
        return newnode;
    }

    // 根据已有节点创建新节点并返回指针
    HuffManTreeNode<T>* CreateNode(HuffManTreeNode<T>* node)
    {
        HuffManTreeNode<T>* newnode = new HuffManTreeNode(node);
        return newnode;
    }

    // 向树中插入新节点
    void Insert(HuffManTreeNode<T>*& node, T data)
    {
        HuffManTreeNode<T>* newnode = CreateNode(data);

        if (newnode == nullptr)
        {
            perror("new fail");
            return;
        }

        if (node->_leftchild == nullptr)
        {
            node->_leftchild = newnode;
        }
        else if (node->_rightchild == nullptr)
        {
            node->_rightchild = newnode;
        }

        return;
    }

    // 向树中插入已有节点
    void Insert(HuffManTreeNode<T>*& node, HuffManTreeNode<T>* temp)
    {
        if (node->_leftchild == nullptr)
        {
            node->_leftchild = CreateNode(temp);
        }
        else if (node->_rightchild == nullptr)
        {
            node->_rightchild = CreateNode(temp);
        }
        return;
    }

    // 重载赋值运算符
    HuffManTreeNode<T>& operator=(const HuffManTreeNode<T>* node)
    {
        if (this == node)
        {
            return *this;
        }

        _data = node->_data;
        _leftchild = node->_leftchild;
        _rightchild = node->_rightchild;

        return *this;
    }

    // 数据成员
    T _data;
    // 左右孩子指针
    HuffManTreeNode<T>* _leftchild;
    HuffManTreeNode<T>* _rightchild;
};

// 中序遍历霍夫曼树
template<class T>
void Inorder(HuffManTreeNode<T>* node)
{
    if (node == nullptr)
    {
        return;
    }

    Inorder(node->_leftchild); // 遍历左子树
    std::cout<< node->_data << " "; // 访问当前节点
    Inorder(node->_rightchild); // 遍历右子树
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120

#include"Huffman.h"

int main()
{
   std::vector<int> vt = {1,45,12,56,78,0,1,3};
   std::sort(vt.begin(),vt.end());

   for(auto e : vt)
   {
       std::cout << e << " ";
   }

   std::cout<<std::endl;

   //创建哈夫曼树
   HuffManTreeNode<int>* node = new HuffManTreeNode(vt[0]+vt[1]);

   node->Insert(node,vt[0]);
   node->Insert(node,vt[1]);

   for(int i = 2 ; i < vt.size(); i++)
   {
       HuffManTreeNode<int>* temp = node;

       node = node->CreateNode(node->_data +vt[i]);

       node->Insert(node,temp);
       node->Insert(node,vt[i]);
   }

   Inorder(node);

   return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

特性

• 最优性：在所有叶子节点数量相同且节点权值已知的二叉树中，哈夫曼树的带权路径长度是最小的。
• 编码效率：哈夫曼编码根据字符出现的频率分配编码，高频字符的编码较短，低频字符的编码较长，从而在整体上达到高效的数据压缩效果。
• 无损编码：哈夫曼编码是一种无损数据压缩方法，可以完全恢复原始数据。
• 自适应性：虽然经典哈夫曼编码基于静态概率模型，但存在变体如自适应哈夫曼编码，能够根据数据流动态调整编码表，适用于数据统计特性随时间变化的情况。

应用

• 数据压缩：广泛应用于文本、图像、音频等数据的无损压缩。
• 通信系统：优化数据传输，减少带宽需求。
• 文件存储：减小文件大小，节约存储空间。
• 编译器：用于词法分析中的关键字识别，通过为常用关键字分配较短编码，提高解析速度。

哈夫曼编码

哈夫曼编码（Huffman Coding）是一种高效的熵编码（Entropy Encoding）方法，用于无损数据压缩。它是基于哈夫曼树（Huffman Tree）构造的一种数据编码方式，由David A. Huffman在1952年提出。以下是哈夫曼编码的核心概念、工作原理以及特点：

核心概念

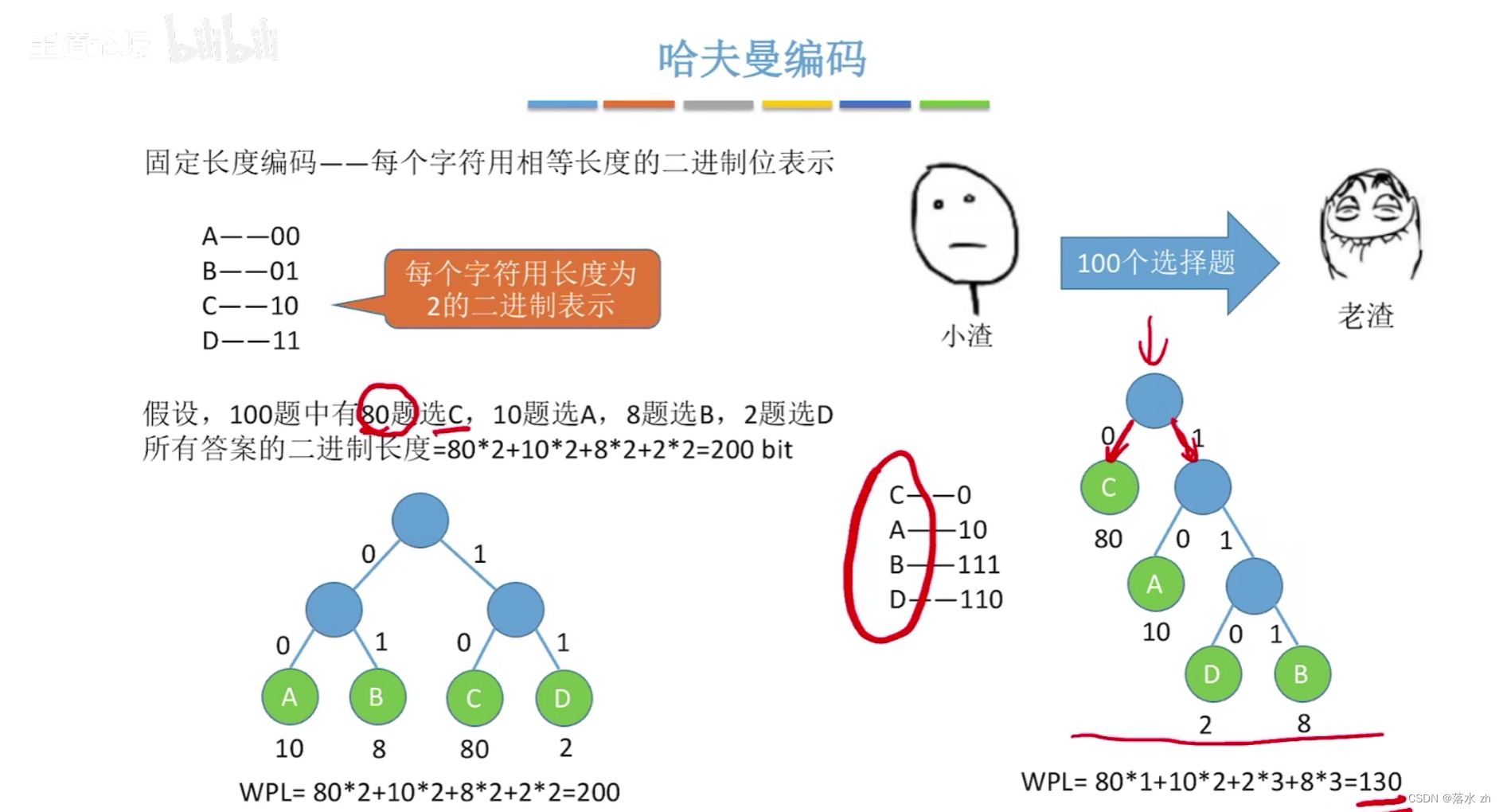
哈夫曼编码的基本思想是根据数据中各个符号（如字符、像素值等）出现的频率来为它们分配不同的编码，出现频率高的符号分配较短的编码，而频率低的符号则分配较长的编码。这样，当整个数据集被编码时，由于高频符号使用的短编码能频繁重复，从而实现整体数据量的压缩。

工作原理

1. 频率统计：首先统计待编码数据中每个符号出现的频率。
2. 构建哈夫曼树：使用频率作为权重，通过哈夫曼树的构造算法（见前述哈夫曼树的构造过程），构建一棵二叉树。在这个过程中，每次都将两个最小频率的节点合并成一个新的节点，新节点的频率是两个子节点频率之和。
3. 生成编码：从哈夫曼树的根到每个叶子节点的路径定义了该叶子节点代表符号的编码。具体来说，向左分支时编码添加一个“0”，向右分支时添加一个“1”。因此，叶子节点越深，其对应的编码就越长。
4. 编码数据：使用生成的哈夫曼编码表对原始数据进行编码，即将数据中的每个符号替换为其对应的编码字符串。

特点

• 无损编码：哈夫曼编码是一种无损数据压缩技术，意味着解码后可以完全恢复原始数据。
• 自适应性：虽然标准哈夫曼编码需要预先知道数据的概率分布，但可以通过动态哈夫曼编码技术，在不知道全部数据的情况下逐步更新编码表，适应数据流的变化。
• 效率：在所有前缀编码（即任意编码都不会是另一个编码的前缀）中，哈夫曼编码提供了理论上的最优平均编码长度，即熵的上限。
• 简单性：尽管编码效率高，哈夫曼编码的算法实现相对直接且易于理解。