纯小白蓝桥杯备赛笔记--DAY4（数学&数据结构&图论）

数学

质因数分解

 int reduce(int prime[],int pn,int n,int rest[])
      {
      int i,k=0;
      for(i=0;i<pn;i++)
           {
           if (n==1) break;
           if (prime[i]*prime[i]>n) {rest[k++]=n;break;}
           while(n%prime[i]==0)
               {
               n/=prime[i];
               rest[k++]=prime[i];
               }
           }
      return k;
      }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

解析：
这段代码是一个名为reduce的函数，它接受四个参数：一个整数数组prime[]，一个整数pn表示数组的长度，一个整数n和一个整数数组rest[]。函数的目的是将整数n分解为质因数，并将这些质因数存储在rest[]数组中。

函数首先初始化两个变量i和k，其中i用于循环遍历prime[]数组，k用于记录rest[]数组的索引。

接下来，函数使用一个for循环遍历prime[]数组。在每次迭代中，它首先检查n是否等于1，如果是，则跳出循环。然后，它检查当前质数的平方是否大于n，如果是，则将n添加到rest[]数组中，并跳出循环。

如果当前质数的平方不大于n，则进入一个while循环。在这个循环中，只要n能被当前质数整除，就将n除以当前质数，并将当前质数添加到rest[]数组中。这个过程会一直重复，直到n不能被当前质数整除为止。

最后，函数返回k，即rest[]数组中的元素个数。

#include<bits/stdc++.h>
using namespace std;

int main()
{
	int n,i;
	cin>>n;
	cout<<n<<"=";
	for(i=2;i<=n;i++)
	{
		while(n!=i)
		{
			if(n%i==0)
			{
				cout<<i<<"*";
				n=n/i;
			}
			else
			break;
		}
	}
	cout<<n<<endl;
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

辗转相除法求最大公约数

inline int gcd(int a,int b)
{
	if(a%b==0)
	return b;
	else
	return (gcd(b,a%b));
}
1
2
3
4
5
6
7

• 简单写法：

int gcb(int a,int b){
 
   return b==0 ? a:gcb(b,a%b);
 
}
1
2
3
4
5

最小公倍数：

int lcm(int a,int b){
		return a/gcd(a,b)*b;//防溢出 ， 很妙啊 ，大家可以记一下
}
1
2
3

快速幂

• 模板

int qmi(int a,int b,int p)//对p取模
{
	int res=1;
	while(b)//只要b不为0，就一直迭代下去 
	{
		if(b&1)res=res*a%p;//b为奇数，乘一个a到答案里
		a=a*a%p,b>>=1;//底数平方，指数除以2 
	}
	return res; 
 } 
1
2
3
4
5
6
7
8
9
10

• 例题：数的幂次–1181

#include<bits/stdc++.h>
using namespace std;

using ll =long long;


ll qmi(ll a,ll b,ll p)//对p取模
{
	ll res=1;
	while(b)//只要b不为0，就一直迭代下去 
	{
		if(b&1)res=res*a%p;//b为奇数，乘一个a到答案里
		a=(ll)a*a%p,b>>=1;//底数平方，指数除以2 
	}
	return res; 
 } 
 int main()
 {
 	int t;
 	cin>>t;
 	while(t--)
 	{
 		ll n,m,p;cin>>n>>m>>p;
 		cout<<qmi(n,m,p)<<endl;
	 }
	 return 0;
 }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

乘法逆元

费马小定理

逆元

乘法逆元

• 例题1：求乘法逆元

#include <bits/stdc++.h>
using namespace std;
using ll=long long;
int t,n;
ll p=1e9+7;
ll qsm(ll a,ll b)
{
  ll res=1;
  while(b)
  {
    if(b&1) res=res*a%p;
    a=a*a%p;b>>=1;
  }
  return res%p;
}
ll inv(ll x)
{
  return qsm(x,p-2);
}
int main()
{
  cin>>t;
  while(t--)
  {
    cin>>n;
    cout<<inv(n)<<endl;
  }
  return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

• 例题2：获胜的概率–3932

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll p=1e9+7;
ll kmi(ll a,ll b)
{
  ll res=1;
  while(b)
  {
    if(b&1) res=res*a%p;
  a=a*a%p;b>>=1;
  }
  return res%p;
  
}
int main()
{ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
  ll n,k;
  cin>>n>>k;
  if(k==0)
  {
    cout<<1<<endl;
    for(int i=2;i<=n;i++) cout<<0<<endl;
  }
  else if(k&1)
  {
    for(int i=1;i<=n;i++)
    {
      if(i&1) cout<<0<<endl;
      else cout<<kmi(n/2,p-2)<<endl;
    }
  }
  else
  {
   for(int i=1;i<=n;i++)
    {
      if(i&1) cout<<kmi((n+1)/2,p-2)<<endl;
      else cout<<0<<endl;
    }
  }

    return 0;
 }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

素数判定与埃式筛法

朴素素数判定法

• 例题：疑似素数-3334

#include<bits/stdc++.h>
using namespace std;
//求和
int f(int x)
{
	int res=0;
	while(x)res+=x%10,x/=10;
	return res;
 } 
bool isPrime(int n)
{
	if(n<2)return false;
	for(int i=2;i<=n/i;i++)
	{
		if(n%i==0)
		return false;
	}
	return true;
	
}
int main()
{
	int n;cin>>n;
	int ans=0;
	for(int i=1;i<=n;i++)
	{
		if(isPrime(f(i)))ans++;
	}
	cout<<ans<<endl;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

埃式筛法

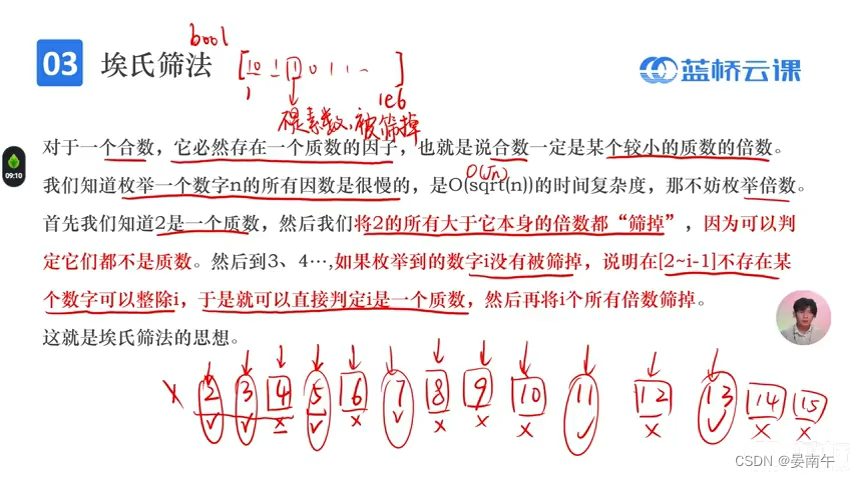
bool vis[N];
vis[0]=vis[1]=true;//被筛掉了
for(int i=2;i<=n;i++)
{
	if(!vis[i])//如果i没有被筛掉，那么进行枚举
	for(int j=2*i;j<=n;j+=i)//枚举倍数 ,每次j变成i的倍数
	vis[j]=ture; 
 } 
1
2
3
4
5
6
7
8

• 例题2：小明的素数对–3205

#include<bits/stdc++.h>
using namespace std;
const int N=1e7;
bool shai[N];vector<int> vec;//将素数筛中杂乱的质数变成排列有序的一个集合，用vector
int main()
{ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
  int n,ans=0;
  cin>>n;
  shai[0]=shai[1]=1;
  for(int i=2;i<=n;i++)
  {
    if(!shai[i])
    {
      vec.push_back(i);
      for(int j=2*i;j<=n;j+=i) shai[j]=1;
    }
    
  }
 
    for(int i=0;i<vec.size();i++)
    for(int j=i+1;j<vec.size();j++)
    {
      if(!shai[vec[j]-vec[i]]) ans++;
    }
    cout<<ans;

    return 0;
 }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

图论

并查集T3:真题–合根植物

• 并查集模版题：
• 注意：不要调用string库。
• 什么是并查集：处理不相交集合的合并问题。
• 用途：求连通子图，求最小生成树的Kruskal算法和求最近公共祖先等。
• 操作：

  • 初始化：
    

  • 查询与合并：
    

  • 查询时对路径进行压缩：
    

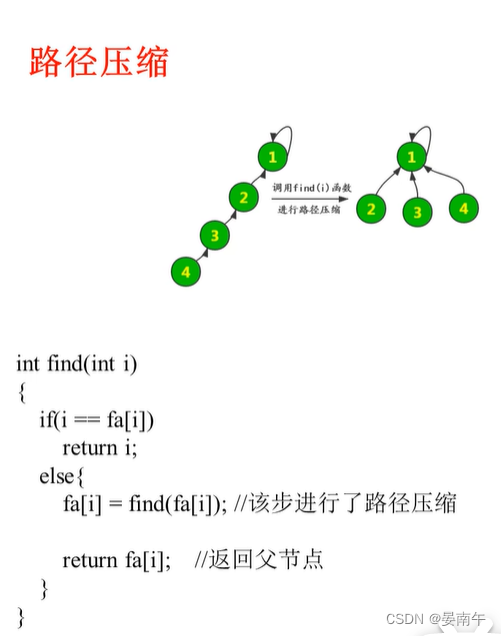
  • 例题
    

#include<cstdio>
#include<cstdlib>
using namespace std;
// 开始的时候定义数组 
#define MAXN 20001
int fa[MAXN];
//最好不要这样定义
 // 初始化
void init(int n)
{
        for(int i=0;i<=n;i++)
        fa[i]=i;
 } 
// 查询 
 int find(int x)
 {
//         递归出口
        if(x==fa[x])
        return x;
        else{
        fa[x]==find(fa[x]);
        return fa[x];
        }
 }
// 合并
void unionn(int i,int j)
{
        int i_fa=find(i);// 找到i的祖先 
        int j_fa=find(j);// 找到j的祖先 
        fa[i_fa]=j_fa ;//i的祖先指向j的祖先 
 }  
// 写主函数
int main()
{
        int m,n,x,y,q;
        scanf("%d",&n);
        init(n);// 初始化这个数组
        scanf("%d",&m); //有m行
        for(int i=1;i<=m;i++)
        {
                scanf("%d%d",&x,&y);
                unionn(x,y);
         } 
         scanf("%d",&q);// 输入q行 
         for(int i=1;i<=q;i++)
         {
                 scanf("%d%d",&x,&y);
                 if(find(x)==find(y))
                 printf("YES\n");
                 else
                 printf("NO\n");
         }

        return 0;         
 } 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

• 合根植物题解：这道题只有一个返回值，所以查询的时候注意不要增加一个返回值了。

#include<stdio.h>
int fa[1000005];
//初始化
 void init(int n)
 {
  for (int i=1;i<=n;i++)
    fa[i] = i;
 }
 // 查询
int find(int x)
{
    if (fa[x] != x)
    {
        int sx = find(fa[x]);
        fa[x] = sx;
    }
    return fa[x];
}
  // 合并
  void unionn(int i,int j)
  {
    int i_fa=find(i);
    int j_fa=find(j);
    fa[i_fa]=j_fa;
   } 
int main(void)
{
  int m,n,q;
  scanf("%d%d%d",&m,&n,&q);
  init(m*n); 
    int x,y;
  for(int i=0;i<q;i++)
  {
    scanf("%d%d",&x,&y);
    unionn(x,y);
  }
  //计数器的设置
   int ans=0;
   for(int i=1;i<=m*n;i++)
   {
    if(i==fa[i])
     {//一个数等于链条的祖先
     ans++; 
  } 
   }
  printf("%d\n",ans);
  return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

Dijkstra

Floyd

基础算法

递归，循环，前缀和，差分

添加链接描述

STL

添加链接描述