- 1强化学习QLearning 进行迷宫游戏和代码_试着将q-learning的思想应用于迷宫问题。(用python代码) 请回答:当state=1时
- 2浙江大学计算机保研条件_记录一下我的保研之路
- 3Hive 初始化 Exception in thread “main“ java.lang.NoSuchMethodError: com.google.common.XXX_hive 4.0 log4j-slf4j-impl-2.18.0.jar
- 4ORB-SLAM3的运行与调试_运行oebslam3
- 5小华最多能得到多少克黄金(87.5%用例)C卷 (Java&&Python&&C++&&Node.js&&C语言)_小华按照地图去寻宝,地图上被划分成m行和n列
- 6达梦数据库管理工具使用_达梦管理工具使用方法
- 7unity移动游戏优化指南_application.targetframerate fixedupdate
- 8大数据毕业设计hadoop+spark+hive知识图谱医生推荐系统 医生数据分析可视化大屏 医生爬虫 医疗可视化 医生大数据 机器学习 计算机毕业设计 机器学习 深度学习 人工智能
- 9《MongoDB权威指南》读书笔记 —— PartⅥ:服务器管理_mongodb db.admincommand( { setparameter 只能在主上
- 10让你至少拿2份offer的软件测试面试题来了(100题带标准答案)_offer办公试题
【自用向 刷题笔记/答案】HDLBITS: Verilog language_verilog项目实践题及答案
赞
踩
Verilog language
basics
1 simple wire
Create a module with one input and one output that behaves like a wire.

module top_module( input in, output out );
assign out = in;
endmodule
- 1
- 2
- 3
- 4
- 5
2 four wires
Create a module with 3 inputs and 4 outputs that behaves like wires that makes these connections:
a -> w
b -> x
b -> y
c -> z
- 1
- 2
- 3
- 4

module top_module (
input a,
input b,
input c,
output w,
output x,
output y,
output z );
assign w = a;
assign x = b;
assign y = b;
assign z = c;
endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
另一种写法:(当位宽对应时)
module top_module(
input a,b,c,
output w,x,y,z );
assign {w,x,y,z} = {a,b,b,c};
endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
3 iNotgate
Create a module that implements a NOT gate.

module top_module(
input in,
output out
);
assign out = ~in;
endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
按位取反和逻辑取反的区别:
“!”表示逻辑求反,“~”表示按位求反。
当对位宽为1的变量进行操作时,这两个操作符的作用是一样的,都是求反。
当对位宽不为1的变量进行操作时,这两个操作符不一样:
- “!”表示~(a[0] | a[1]),只有当a的每一位都为0时,结果才为1,条件判断中 if(!a) 等价于 if(a == 0);
- “~”表示对每一位按位取反,只有当a的每一位都为1时,结果才为0。
4 Andgate
Create a module that implements an AND gate.

module top_module(
input a,
input b,
output out );
assign out = a & b;
endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
5 Norgate
Create a module that implements a NOR gate. A NOR gate is an OR gate with its output inverted. A NOR function needs two operators when written in Verilog.

module top_module(
input a,
input b,
output out );
assign out = ~(a | b);
endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
或非门,先或再非即可
与非门,先与再非即可
6 Xnorgate
Create a module that implements an XNOR gate.

module top_module(
input a,
input b,
output out );
assign out = ~(a ^ b);
endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
^为同或运算,若是异或,先同或再取反
7 Declaring wires
Implement the following circuit. Create two intermediate wires (named anything you want) to connect the AND and OR gates together. Note that the wire that feeds the NOT gate is really wire out, so you do not necessarily need to declare a third wire here. Notice how wires are driven by exactly one source (output of a gate), but can feed multiple inputs.

`default_nettype none module top_module( input a, input b, input c, input d, output out, output out_n ); wire a_and_b, c_and_d; assign a_and_b = a & b; assign c_and_d = c & d; assign out = a_and_b | c_and_d; assign out_n = ~out; endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
8 7458
Create a module with the same functionality as the 7458 chip. It has 10 inputs and 2 outputs. You may choose to use an assign statement to drive each of the output wires, or you may choose to declare (four) wires for use as intermediate signals, where each internal wire is driven by the output of one of the AND gates. For extra practice, try it both ways.

module top_module ( input p1a, p1b, p1c, p1d, p1e, p1f, output p1y, input p2a, p2b, p2c, p2d, output p2y ); wire p1abc_and, p1def_and; wire p2ab_and, p2cd_and; assign p1abc_and = p1a & p1b & p1c; assign p1def_and = p1d & p1e & p1f; assign p2ab_and = p2a & p2b; assign p2cd_and = p2c & p2d; assign p1y = p1abc_and | p1def_and; assign p2y = p2ab_and | p2cd_and; endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
vectors
1 Vector0
Build a circuit that has one 3-bit input, then outputs the same vector, and also splits it into three separate 1-bit outputs. Connect output o0 to the input vector’s position 0, o1 to position 1, etc.

module top_module (
input wire [2:0] vec,
output wire [2:0] outv,
output wire o2,
output wire o1,
output wire o0 ); // Module body starts after module declaration
assign outv[2:0] = vec[2:0];
assign o0 = vec[0];
assign o1 = vec[1];
assign o2 = vec[2];
endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
2 Vector1
Build a combinational circuit that splits an input half-word (16 bits, [15:0] ) into lower [7:0] and upper [15:8] bytes.
module top_module (
input [15:0] in,
output [7:0] out_hi,
output [7:0] out_lo
);
assign out_hi = in[15:8];
assign out_lo = in[7:0];
// assign {out_hi, out_lo} = in;
endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
向量的声明方式
Vectors must be declared:
type [upper:lower] vector_name;
- 1
some example:
wire [7:0] w; // 8-bit wire reg [4:1] x; // 4-bit reg output reg [0:0] y; // 1-bit reg that is also an output port (this is still a vector) input wire [3:-2] z; // 6-bit wire input (negative ranges are allowed) output [3:0] a; // 4-bit output wire. Type is 'wire' unless specified otherwise. wire [0:7] b; // 8-bit wire where b[0] is the most-significant bit.
- 1
- 2
- 3
- 4
- 5
- 6
当一个向量以某一特定的字节序被声明(如:小端字节序vec[3:0],大端字节序vec[0:3]),采用其他字节序去使用它会是非法的,如wire [3:0] vec不能写作vec[0:3]。为避免错误,建议在编程时保证字节序一致。
隐式声明
若采用隐式声明引入某变量,可能会导致错误,这是因为隐式声明通常为1位wire类型,使用向量对其进行赋值时只有最低参与赋值。
wire [2:0] a, c; // Two vectors assign a = 3'b101; // a = 101 assign b = a; // b = 1 implicitly-created wire assign c = b; // c = 001 <-- bug
- 1
- 2
- 3
- 4
同时,在module的声明时,若采用隐式声明,默认数据为1位wire,若连接的端口为向量,则会导致错误。
my_module i1 (d,e); // d and e are implicitly one-bit wide if not declared. // This could be a bug if the port was intended to be a vector.
- 1
- 2
向量的打包维度与非打包维度
写在向量名前面的为打包维度x,写在向量名后面的为非打包维度y,可以理解为:y个位宽为x的向量。
reg [7:0] mem [255:0]; // 256 unpacked elements, each of which is a 8-bit packed vector of reg. reg mem2 [28:0]; // 29 unpacked elements, each of which is a 1-bit reg.
- 1
- 2
部分选择
可以直接采用assign对整个张量数据进行赋值:
wire [7:0] w; wire [3:0] a; assign w = a;
- 1
- 2
- 3
- 4
将4位向量a赋值给8位向量w,如长度不一样,则会进行补0或者截断操作。
3 Vector2 (part select)
A 32-bit vector can be viewed as containing 4 bytes (bits [31:24], [23:16], etc.). Build a circuit that will reverse the byte ordering of the 4-byte word.
AaaaaaaaBbbbbbbbCcccccccDddddddd => DdddddddCcccccccBbbbbbbbAaaaaaaa
module top_module (
input [31:0] in,
output [31:0] out
);
assign out[31:24] = in[ 7: 0];
assign out[23:16] = in[15: 8];
assign out[15: 8] = in[23:16];
assign out[ 7: 0] = in[31:24];
endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
另一种写法:
module top_module(
input [31:0] in,
output [31:0] out );
assign {out[31:24],out[23:16],out[15:8],out[7:0]} =
{in[7:0],in[15:8],in[23:16],in[31:24]};
endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
4 Vectorgates
module top_module(
input [2:0] a,
input [2:0] b,
output [2:0] out_or_bitwise,
output out_or_logical,
output [5:0] out_not
);
assign out_or_bitwise[2:0] = a | b;
assign out_or_logical = a || b;
assign out_not[5:3] = ~b;
assign out_not[2:0] = ~a;
endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
逻辑操作符
逻辑操作符的结果是一个1位的值:0假,1真,X不确定,Z高阻态
- 如果一个值不为0,那么他在逻辑运算中等价为1
- 如果此值为0,那么等价为0
- 如果此值有X,当矢量中只需有一位为1,那么就代表“1”
逻辑与(&&)
//逻辑与: wire c; wire [3:0] a=4’b0101; wire [3:0] b=4’b1110; c=a && b; //c=1 //按位与1: wire [3:0] c; wire [3:0] a=4’b0101; wire [3:0] b=4’b0000; c=a & b; //c=4’b0000 //按位与2 wire [3:0] c; wire [3:0] a=4’b0101; wire [3:0] b=4’b0100; wire c=a & b; //c=0100
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
逻辑或(||)
逻辑非(!)
“!”表示只有当a的每一位都为0时,结果才为1,条件判断中 if(!a) 等价于 if(a == 0);
5 Gates4
Build a combinational circuit with four inputs, in[3:0].
There are 3 outputs:
- out_and: output of a 4-input AND gate.
- out_or: output of a 4-input OR gate.
- out_xor: output of a 4-input XOR gate.
module top_module(
input [3:0] in,
output out_and,
output out_or,
output out_xor
);
assign out_and = &in[3:0];
assign out_or = |in[3:0];
assign out_xor = ^in[3:0];
endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
缩减操作符(规约操作符)
| Operator | Description |
|---|---|
| & | and |
| ~& | nand |
| | | or |
| ~| | nor |
| ^ | xor |
| ^~ or ~^ | xnor |
缩减操作符只有一个操作数,它对这个向量逐位进行逻辑操作,产生一位的运算结果,对于n元素的向量,等同于n输入逻辑门。
6 Vector3
There are four 8-bit output vectors: w, x, y, and z, for 32 bits of output. The output should be a concatenation of the input vectors followed by two 1 bits:

module top_module (
input [4:0] a, b, c, d, e, f,
output [7:0] w, x, y, z );//
assign {w[7:0], x[7:0], y[7:0], z[7:0] } = { a[4:0], b[4:0], c[4:0], d[4:0], e[4:0], f[4:0],2'b11};
endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
向量的合并与分割
在两边位宽匹配的情况下,可以对向量进行合并或分割,进而执行赋值操作。
input [15:0] in; output [23:0] out; // 以下两种操作指定了位宽,为部分位数赋值,未提及的部分位则为X态。 assign {out[7:0], out[15:8]} = in; // Swap two bytes. Right side and left side are both 16-bit vectors. assign out[15:0] = {in[7:0], in[15:8]}; // This is the same thing. // 而直接赋值时,两边位宽不统一,则会进行补0或者截断操作。 assign out = {in[7:0], in[15:8]}; // This is different. The 16-bit vector on the right is extended to // match the 24-bit vector on the left, so out[23:16] are zero.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
7 Vectorr
Given an 8-bit input vector [7:0], reverse its bit ordering.
module top_module(
input [7:0] in,
output [7:0] out
);
assign {out[0],out[1],out[2],out[3],out[4],out[5],out[6],out[7]} = {in[7],in[6],in[5],in[4],in[3],in[2],in[1],in[0]};
endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
实际上,in本身采用了[7:0]的字节序,可以直接
module top_module (
input [7:0] in,
output [7:0] out
);
assign {out[0],out[1],out[2],out[3],out[4],out[5],out[6],out[7]} = in;
endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
用always block也行,里面写个for循环
module top_module (
input [7:0] in,
output [7:0] out
);
always @(*) begin
for (int i=0; i<8; i++) // int is a SystemVerilog type. Use integer for pure Verilog.
out[i] = in[8-i-1];
end
endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
Verilog中还有一种generate语句,常用于编写可配置的、可综合的RTL的设计结构。它可用于创建模块的多个实例化,或者有条件的实例化代码块。
我们常用generate语句做三件事情。一个是用来构造循环结构,用来多次实例化某个模块。一个是构造条件generate结构,用来在多个块之间最多选择一个代码块,条件generate结构包含if–generate结构或者case–generate形式。还有一个是用来断言。
genvar 循环变量名; generate // generate循环语句 // generate 条件语句 // generate 分支语句 // 嵌套的generate语句 endgenerate
- 1
- 2
- 3
- 4
- 5
- 6
- 7
在此例中,采用generate构建循环语句,他的用法为:
- 先在genvar声明中声明循环中使用的索引变量名
- generate语句中定义的for语句,必须要有begin,为后续增加标签做准备。
- begin必须要有名称,也就是必须要有标签,因为标签会作为generate循环的实例名称。
module top_module (
input [7:0] in,
output [7:0] out
);
generate
genvar i;
for (i=0; i<8; i = i+1) begin: my_block_name
assign out[i] = in[8-i-1];
end
endgenerate
endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
8 Vector4
Build a circuit that sign-extends an 8-bit number to 32 bits. This requires a concatenation of 24 copies of the sign bit (i.e., replicate bit[7] 24 times) followed by the 8-bit number itself.
module top_module (
input [7:0] in,
output [31:0] out );//
assign out = { {24{in[7]}} , in };//容易出错的地方:24{in[7]}外也要加{}
endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
9 Vector5
As the diagram shows, this can be done more easily using the replication and concatenation operators.
- The top vector is a concatenation of 5 repeats of each input
- The bottom vector is 5 repeats of a concatenation of the 5 inputs

module top_module (
input a, b, c, d, e,
output [24:0] out );//
wire [4:0] temp;
assign temp = {a,b,c,d,e};
assign out = {~({5{a}}^temp),~({5{b}}^temp),~({5{c}}^temp),~({5{d}}^temp),~({5{e}}^temp)};
endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
答案提供的一种可读性更高的写法:
module top_module (
input a, b, c, d, e,
output [24:0] out
);
wire [24:0] top, bottom;
assign top = { {5{a}}, {5{b}}, {5{c}}, {5{d}}, {5{e}} };
assign bottom = {5{a,b,c,d,e}};
assign out = ~top ^ bottom; // Bitwise XNORs
endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
答案提供的一种更简化的写法:
module top_module (
input a, b, c, d, e,
output [24:0] out
);
assign out = ~{ {5{a}}, {5{b}}, {5{c}}, {5{d}}, {5{e}} } ^ {5{a,b,c,d,e}};
endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
Module: Hierarchy
1 module
You may connect signals to the module by port name or port position. For extra practice, try both methods.

通过位置的方式例化module:
module top_module ( input a, input b, output out );
mod_a instance1 ( a, b, out );
endmodule
- 1
- 2
- 3
通过对应变量名的方式例化module:
module top_module ( input a, input b, output out );
mod_a instance2 ( .in1(a), .in2(b), .out(out) );
endmodule
- 1
- 2
- 3
2 module pos
You are given a module named mod_a that has 2 outputs and 4 inputs, in that order. You must connect the 6 ports by position to your top-level module’s ports out1, out2, a, b, c, and d, in that order.
You are given the following module:
module mod_a ( output, output, input, input, input, input );
- 1

module top_module (
input a,
input b,
input c,
input d,
output out1,
output out2
);
mod_a amod ( out1, out2, a, b, c, d );
endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
3 module name
You are given a module named mod_a that has 2 outputs and 4 inputs, in some order. You must connect the 6 ports by name to your top-level module’s ports:
| Port in mod_a | Port in top_module |
|---|---|
output out1 | out1 |
output out2 | out2 |
input in1 | a |
input in2 | b |
input in3 | c |
input in4 | d |
You are given the following module:
module mod_a ( output out1, output out2, input in1, input in2, input in3, input in4);
- 1

module top_module ( input a, input b, input c, input d, output out1, output out2 ); mod_a amod( .in1(a), .in2(b), .in3(c), .in4(d), .out1(out1), .out2(out2) ); endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
4 module shift
You are given a module my_dff with two inputs and one output (that implements a D flip-flop). Instantiate three of them, then chain them together to make a shift register of length 3. The clk port needs to be connected to all instances.
The module provided to you is: module my_dff ( input clk, input d, output q );
Note that to make the internal connections, you will need to declare some wires. Be careful about naming your wires and module instances: the names must be unique.

module top_module ( input clk, input d, output q );
wire q1, q2;
my_dff dff1( clk, d, q1 );
my_dff dff2( clk, q1, q2 );
my_dff dff3( clk, q2, q );
endmodule
- 1
- 2
- 3
- 4
- 5
- 6
5 module shift8
You are given a module my_dff8 with two inputs and one output (that implements a set of 8 D flip-flops). Instantiate three of them, then chain them together to make a 8-bit wide shift register of length 3. In addition, create a 4-to-1 multiplexer (not provided) that chooses what to output depending on sel[1:0]: The value at the input d, after the first, after the second, or after the third D flip-flop. (Essentially, sel selects how many cycles to delay the input, from zero to three clock cycles.)
The module provided to you is: module my_dff8 ( input clk, input [7:0] d, output [7:0] q );
The multiplexer is not provided. One possible way to write one is inside an always block with a case statement inside. (See also: mux9to1v)

module top_module ( input clk, input [7:0] d, input [1:0] sel, output [7:0] q ); wire [7:0] q1; wire [7:0] q2; wire [7:0] q3; my_dff8 dff1( clk, d, q1 ); my_dff8 dff2( clk, q1, q2 ); my_dff8 dff3( clk, q2, q3 ); always @(*) begin case(sel) 0:begin q <= d; end 1:begin q <= q1; end 2:begin q <= q2; end 3:begin q <= q3; end endcase end endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
简单的写法:
module top_module ( input clk, input [7:0] d, input [1:0] sel, output reg [7:0] q ); wire [7:0] o1, o2, o3; // output of each my_dff8 // Instantiate three my_dff8s my_dff8 d1 ( clk, d, o1 ); my_dff8 d2 ( clk, o1, o2 ); my_dff8 d3 ( clk, o2, o3 ); // This is one way to make a 4-to-1 multiplexer always @(*) // Combinational always block case(sel) 2'h0: q = d; 2'h1: q = o1; 2'h2: q = o2; 2'h3: q = o3; endcase endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
always block
verilog中有always和initial两种procedure,每个initial block和always block代表独立的执行过程,每个执行过程从仿真时间0开始执行并且两种语句不能嵌套使用。 他们的最大区别是,initial语句只执行一次,而always语句则不断重复的活动着,每当敏感列表发生变化,always语句就会相应并执行。
建议在组合逻辑使用always block时,采用自动敏感列表(*)。在时序逻辑使用always block时,采用边缘触发的敏感列表,如(posedge clk)。
// 边沿触发 always@(posedge clk or negedge rst) begin .... end // 电平触发 always@(a or b or c) begin .... end // 自动敏感列表 // 以下的两个always block,他们功能相同 always@(a,b,c,d,e,f,g,h,r,m) begin out1 = a?(b+c):(d+e); out2 = f?(g+h):(r+m) end always@(*) begin out1 = a?(b+c):(d+e); out2 = f?(g+h):(r+m) end
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
case语句常用来构造复用器/选通器(MUX),其语法为:
case (<expression>)
case_item1 : <single statement>
case_item2,
case_item3 : <single statement>
case_item4 : begin
<multiple statements>
end
default : <statement>
endcase
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
6 Module add
You are given a module add16 that performs a 16-bit addition. Instantiate two of them to create a 32-bit adder. One add16 module computes the lower 16 bits of the addition result, while the second add16 module computes the upper 16 bits of the result, after receiving the carry-out from the first adder. Your 32-bit adder does not need to handle carry-in (assume 0) or carry-out (ignored), but the internal modules need to in order to function correctly. (In other words, the add16 module performs 16-bit a + b + cin, while your module performs 32-bit a + b).
Connect the modules together as shown in the diagram below. The provided module add16 has the following declaration:
module add16 ( input[15:0] **a**, input[15:0] **b**, input **cin**, output[15:0] **sum**, output **cout** );
- 1

module top_module( input [31:0] a, input [31:0] b, output [31:0] sum ); wire c16; add16 addl( .cin(0), .a(a[15:0]), .b(b[15:0]), .cout(c16), .sum(sum[15:0]) ); add16 addu( .cin(c16), .a(a[31:16]), .b(b[31:16]), .sum(sum[31:16]) ); endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
7 Module fadd
In this exercise, you will create a circuit with two levels of hierarchy. Your top_module will instantiate two copies of add16 (provided), each of which will instantiate 16 copies of add1 (which you must write). Thus, you must write two modules: top_module and add1.
Like module_add, you are given a module add16 that performs a 16-bit addition. You must instantiate two of them to create a 32-bit adder. One add16 module computes the lower 16 bits of the addition result, while the second add16 module computes the upper 16 bits of the result. Your 32-bit adder does not need to handle carry-in (assume 0) or carry-out (ignored).
Connect the add16 modules together as shown in the diagram below. The provided module add16 has the following declaration:
module add16 ( input[15:0] a, input[15:0] b, input cin, output[15:0] sum, output cout );
- 1
Within each add16, 16 full adders (module add1, not provided) are instantiated to actually perform the addition. You must write the full adder module that has the following declaration:
module add1 ( input a, input b, input cin, output sum, output cout );
Recall that a full adder computes the sum and carry-out of a+b+cin.
In summary, there are three modules in this design:
- top_module — Your top-level module that contains two of…
- add16, provided — A 16-bit adder module that is composed of 16 of…
- add1 — A 1-bit full adder module.
module top_module ( input [31:0] a, input [31:0] b, output [31:0] sum );// wire c16; add16 addl( .cin(0), .a(a[15:0]), .b(b[15:0]), .cout(c16), .sum(sum[15:0]) ); add16 addu( .cin(c16), .a(a[31:16]), .b(b[31:16]), .sum(sum[31:16]) ); endmodule module add1 ( input a, input b, input cin, output sum, output cout ); assign {cout,sum} = a + b + cin; endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
如果没有给定add16,则需要使用16个add1构建add16:



module top_module ( input [31:0] a, input [31:0] b, output [31:0] sum );// wire c16; add16 addl( .cin(0), .a(a[15:0]), .b(b[15:0]), .cout(c16), .sum(sum[15:0]) ); add16 addu( .cin(c16), .a(a[31:16]), .b(b[31:16]), .sum(sum[31:16]) ); endmodule module add1 ( input a, input b, input cin, output sum, output cout ); assign {cout,sum} = a + b + cin; endmodule module add16 ( input [15:0] a, input [15:0] b, input cin, output [15:0] sum, output cout); wire [15:0] cout_add1; add1 add_0( .a(a[0]), .b(b[0]), .cin(cin), .sum(sum[0]), .cout(cout_add1[0])); add1 add_1( .a(a[1]), .b(b[1]), .cin(cout_add1[0]), .sum(sum[1]), .cout(cout_add1[1])); add1 add_2( .a(a[2]), .b(b[2]), .cin(cout_add1[1]), .sum(sum[2]), .cout(cout_add1[2])); add1 add_3( .a(a[3]), .b(b[3]), .cin(cout_add1[2]), .sum(sum[3]), .cout(cout_add1[3])); add1 add_4( .a(a[4]), .b(b[4]), .cin(cout_add1[3]), .sum(sum[4]), .cout(cout_add1[4])); add1 add_5( .a(a[5]), .b(b[5]), .cin(cout_add1[4]), .sum(sum[5]), .cout(cout_add1[5])); add1 add_6( .a(a[6]), .b(b[6]), .cin(cout_add1[5]), .sum(sum[6]), .cout(cout_add1[6])); add1 add_7( .a(a[7]), .b(b[7]), .cin(cout_add1[6]), .sum(sum[7]), .cout(cout_add1[7])); add1 add_8( .a(a[8]), .b(b[8]), .cin(cout_add1[7]), .sum(sum[8]), .cout(cout_add1[8])); add1 add_9( .a(a[9]), .b(b[9]), .cin(cout_add1[8]), .sum(sum[9]), .cout(cout_add1[9])); add1 add_10( .a(a[10]), .b(b[10]), .cin(cout_add1[9]), .sum(sum[10]), .cout(cout_add1[10])); add1 add_11( .a(a[11]), .b(b[11]), .cin(cout_add1[10]), .sum(sum[11]), .cout(cout_add1[11])); add1 add_12( .a(a[12]), .b(b[12]), .cin(cout_add1[11]), .sum(sum[12]), .cout(cout_add1[12])); add1 add_13( .a(a[13]), .b(b[13]), .cin(cout_add1[12]), .sum(sum[13]), .cout(cout_add1[13])); add1 add_14( .a(a[14]), .b(b[14]), .cin(cout_add1[13]), .sum(sum[14]), .cout(cout_add1[14])); add1 add_15( .a(a[15]), .b(b[15]), .cin(cout_add1[14]), .sum(sum[15]), .cout(cout)); endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
8 Module cseladd
One drawback of the ripple carry adder (See previous exercise) is that the delay for an adder to compute the carry out (from the carry-in, in the worst case) is fairly slow, and the second-stage adder cannot begin computing its carry-out until the first-stage adder has finished. This makes the adder slow.
全加器的弊端:carry位的极高延迟——由于每一位运算需要依赖前一位运算的carry值,当前一位未完成运算时,则无法进行下一位的运算,高位需要等待所有低位的carry位运算结果,carry位的传播会给电路带来极大的延迟。
本例中的电路叫做选择进位加法器,第一级正常运算,第二级加法器包含两个16位加法器电路,一个假设进位为0,一个假设进位为1,最后使用复用器选择正确的结果,是牺牲面积换速度的例子。
One improvement is a carry-select adder, shown below. The first-stage adder is the same as before, but we duplicate the second-stage adder, one assuming carry-in=0 and one assuming carry-in=1, then using a fast 2-to-1 multiplexer to select which result happened to be correct.
In this exercise, you are provided with the same module add16 as the previous exercise, which adds two 16-bit numbers with carry-in and produces a carry-out and 16-bit sum. You must instantiate three of these to build the carry-select adder, using your own 16-bit 2-to-1 multiplexer.
Connect the modules together as shown in the diagram below. The provided module add16 has the following declaration:
module add16 ( input[15:0] a, input[15:0] b, input cin, output[15:0] sum, output cout );
- 1

module top_module( input [31:0] a, input [31:0] b, output [31:0] sum ); wire cout_u; wire [15:0] sum_u0, sum_u1; add16 addl( .cin(0), .a(a[15:0]), .b(b[15:0]), .cout(cout_u), .sum(sum[15:0]) ); add16 add_u0( .cin(0), .a(a[31:16]), .b(b[31:16]), .sum(sum_u0) ); add16 add_u1( .cin(1), .a(a[31:16]), .b(b[31:16]), .sum(sum_u1) ); always @(*) begin case(cout_u) 0: sum[31:16] = sum_u0; 1: sum[31:16] = sum_u1; endcase end endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
超前进位加法器
此外,在电路的层次上,还有一种超前进位加法器,通过添加一个组合电路,提前计算出进位,我们对此电路进行推导,已知第i位加法器的Co与Ci存在以下的表达关系:
C o i = A i B i + ( A i + B i ) C i i Co_i = A_iB_i + (A_i+B_i)Ci_i Coi=AiBi+(Ai+Bi)Cii
我们定义生成信号:
G i = A i B i G_i = A_i B_i Gi=AiBi
传输信号:
P i = A i + B i P_i = A_i + B_i Pi=Ai+Bi
那么:
C o i = G i + P i C i i Co_i =G_i + P_i Ci_i Coi=Gi+PiCii
以一个四位超前进位加法器为例,依次递推,有:
C 0 = C i n C_0 = C_in C0=CinC 1 = G 0 + P 0 C 0 C_1 = G_0 + P_0 C_0 C1=G0+P0C0
C 2 = G 1 + P 1 ( G 0 + P 0 C 0 ) C_2 =G_1 + P_1 (G_0 + P_0 C_0) C2=G1+P1(G0+P0C0)
C 3 = G 2 + P 2 ( G 1 + P 1 ( G 0 + P 0 C 0 ) ) C_3 = G_2 + P_2 (G_1 + P_1 (G_0 + P_0 C_0)) C3=G2+P2(G1+P1(G0+P0C0))
采用Verilog语言描述:
module top_module ( input [3:0] a, input [3:0] b, input cin, output [3:0] sum, output c_out ); wire [3:0] g,p; assign g = a & b; assign p = a | b; wire [4:0] c_bit; assign c_bit[0] = cin; assign c_bit[1] = g[0]|(p[0]&c_bit[0]); assign c_bit[2] = g[1]|(p[1]&g[0])|(p[1]&p[0]&c_bit[0]); assign c_bit[3] = g[2]|(p[2]&g[1])|(p[2]&p[1]&g[0])|(p[2]&p[1]&p[0]&c_bit[0]); assign c_bit[4] = g[3]|(p[3]&g[2])|(p[3]&p[2]&g[1])|(p[3]&p[2]&p[1]&g[0])|(p[3]&p[2]&p[1]&p[0]&c_bit[0]); assign sum = a ^ b ^ c_bit[3:0]; assign c_out = c_bit[4]; endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
由于高位的进位输出表达式(积之和式)涉及的变量更多,对应的逻辑电路连线会变得更复杂,而且在实际应用中会遭遇逻辑门的扇入问题。所以出于对成本的考虑,有必要对位数过高的全加器进行逻辑划分,如将六十四位全加器分为四个十六位超前进位加法器来实现,以此来实现成本和性能的平衡。
9 Module addsub
An adder-subtractor can be built from an adder by optionally negating one of the inputs, which is equivalent to inverting the input then adding 1. The net result is a circuit that can do two operations: (a + b + 0) and (a + ~b + 1). See Wikipedia if you want a more detailed explanation of how this circuit works.
Build the adder-subtractor below.
You are provided with a 16-bit adder module, which you need to instantiate twice:
module add16 ( input[15:0] a, input[15:0] b, input cin, output[15:0] sum, output cout );
- 1
Use a 32-bit wide XOR gate to invert the b input whenever sub is 1. (This can also be viewed as b[31:0] XORed with sub replicated 32 times. See replication operator.). Also connect the sub input to the carry-in of the adder.

module top_module( input [31:0] a, input [31:0] b, input sub, output [31:0] sum ); wire c16; wire [31:0] b_inv; assign b_inv = b ^ {32{sub}}; add16 addl( .cin(sub), .a(a[15:0]), .b(b_inv[15:0]), .cout(c16), .sum(sum[15:0]) ); add16 addu( .cin(c16), .a(a[31:16]), .b(b_inv[31:16]), .sum(sum[31:16]) ); endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
procedures
1 Alwaysblock1
Build an AND gate using both an assign statement and a combinational always block. (Since assign statements and combinational always blocks function identically, there is no way to enforce that you’re using both methods. But you’re here for practice, right?..)
// synthesis verilog_input_version verilog_2001
module top_module(
input a,
input b,
output wire out_assign,
output reg out_alwaysblock
);
assign out_assign = a & b;
always @(*) begin
out_alwaysblock <= a & b;
end
endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
2 Alwaysblock2
Build an XOR gate three ways, using an assign statement, a combinational always block, and a clocked always block. Note that the clocked always block produces a different circuit from the other two: There is a flip-flop so the output is delayed.

// synthesis verilog_input_version verilog_2001 module top_module( input clk, input a, input b, output wire out_assign, output reg out_always_comb, output reg out_always_ff ); assign out_assign = a ^ b; always @(*) begin out_always_comb = a ^ b; end always @(posedge clk) begin out_always_ff <= a ^ b; end endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
时序逻辑与组合逻辑下的always block
Combinational:
always @(*)// 表示自动补全敏感列表
- 1
Clocked:
always @(posedge clk)
- 1
三种assignment语句
在进程外使用:
- 连续赋值语句 assign
在进程内使用:
- 阻塞性赋值 x = y,多个阻塞性赋值语句会按顺序执行
- 非阻塞性赋值 x<=y,多个非阻塞性赋值语句会并行执行
建议在一个组合逻辑always块中,使用阻塞语句,在一个时序逻辑always块中,使用非阻塞语句。这并不是绝对的,但是建议这样做以提升代码规范性,同时,切忌在一个always block中混用两种赋值语句。
3 Always if
Build a 2-to-1 mux that chooses between a and b. Choose b if both sel_b1 and sel_b2 are true. Otherwise, choose a. Do the same twice, once using assign statements and once using a procedural if statement.
| sel_b1 | sel_b2 | out_assign out_always |
|---|---|---|
| 0 | 0 | a |
| 0 | 1 | a |
| 1 | 0 | a |
| 1 | 1 | b |
// synthesis verilog_input_version verilog_2001 module top_module( input a, input b, input sel_b1, input sel_b2, output wire out_assign, output reg out_always ); assign out_assign = ( {sel_b1,sel_b2} != 2'b11 ) ? a : b; always @(*) begin if (( sel_b1 == 1 )&( sel_b2 == 1 )) begin out_always = b; end else begin out_always = a; end end endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
二路选通器(复用器)的一个简便写法:
always @(*) begin
if (condition) begin
out = x;
end
else begin
out = y;
end
end
// 等同于
assign out = (condition) ? x : y;
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
4 Always if2
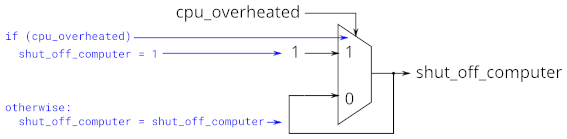
The following code contains incorrect behaviour that creates a latch. Fix the bugs so that you will shut off the computer only if it’s really overheated, and stop driving if you’ve arrived at your destination or you need to refuel.
This is the circuit described by the code, not the circuit you want to build.
always @(*) begin
if (cpu_overheated)
shut_off_computer = 1;
end
always @(*) begin
if (~arrived)
keep_driving = ~gas_tank_empty;
end
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
上面的代码主要的bug在于if之后没有else,所以没有确定所有的情况,在敏感列表被触发时没有相应的赋值语句,导致了latch。
// synthesis verilog_input_version verilog_2001 module top_module ( input cpu_overheated, output reg shut_off_computer, input arrived, input gas_tank_empty, output reg keep_driving ); // always @(*) begin if (cpu_overheated) shut_off_computer = 1; else shut_off_computer = 0; end always @(*) begin if (arrived | gas_tank_empty) keep_driving = 0; else keep_driving = 1; end endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21

上图所示电路,在电脑过载时关闭系统,在没油或者到达时停下车,能够实现相应的功能,并保证没有latch。
latch锁存器
电路设计中要尽量避免出现latch,这是由于:
- latch对毛刺敏感。
- 不能异步复位,在上电后会处于不确定的状态
- latch会影响静态时序分析
- 在FPGA中,基本单元由查找表和触发器组成,生成锁存器会需要更多的资源
latch主要产生的原因:
核心问题在于当组合逻辑条件未给全时,由于并未设定某一情况下信号的变化,那么默认该状态下信号不变,从而综合出锁存器,保留原有值。
coding时会导致latch产生的情况:
- case语句没有default
- if后没有else
- alwaysblock中敏感列表遗漏,因此强烈建议在组合逻辑编程中采用always @(*)
5 always case
Case statements are more convenient than if statements if there are a large number of cases. So, in this exercise, create a 6-to-1 multiplexer. When sel is between 0 and 5, choose the corresponding data input. Otherwise, output 0. The data inputs and outputs are all 4 bits wide.
// synthesis verilog_input_version verilog_2001 module top_module ( input [2:0] sel, input [3:0] data0, input [3:0] data1, input [3:0] data2, input [3:0] data3, input [3:0] data4, input [3:0] data5, output reg [3:0] out );// always@(*) begin // This is a combinational circuit case(sel) 3'b 000: out = data0; 3'b 001: out = data1; 3'b 010: out = data2; 3'b 011: out = data3; 3'b 100: out = data4; 3'b 101: out = data5; default out = 3'b 000; endcase end endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
6 Always case2
A priority encoder is a combinational circuit that, when given an input bit vector, outputs the position of the first 1 bit in the vector. For example, a 8-bit priority encoder given the input 8'b10010000 would output 3'd4, because bit[4] is first bit that is high.
Build a 4-bit priority encoder. For this problem, if none of the input bits are high (i.e., input is zero), output zero. Note that a 4-bit number has 16 possible combinations.
// synthesis verilog_input_version verilog_2001 module top_module ( input [3:0] in, output reg [1:0] pos ); always @(*) begin case (in) 4'b0000 : pos = 0; 4'b0001 : pos = 0; 4'b0010 : pos = 1; 4'b0011 : pos = 0; 4'b0100 : pos = 2; 4'b0101 : pos = 0; 4'b0110 : pos = 1; 4'b0111 : pos = 0; 4'b1000 : pos = 3; 4'b1001 : pos = 0; 4'b1010 : pos = 1; 4'b1011 : pos = 0; 4'b1100 : pos = 2; 4'b1101 : pos = 0; 4'b1110 : pos = 1; 4'b1111 : pos = 0; default: pos = 0; endcase end endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
7 Always casez
Build a priority encoder for 8-bit inputs. Given an 8-bit vector, the output should report the first bit in the vector that is 1. Report zero if the input vector has no bits that are high. For example, the input 8’b10010000 should output 3’d4, because bit[4] is first bit that is high.
From the previous exercise (always_case2), there would be 256 cases in the case statement. We can reduce this (down to 9 cases) if the case items in the case statement supported don’t-care bits. This is what casez is for: It treats bits that have the value z as don’t-care in the comparison.
For example, this would implement the 4-input priority encoder from the previous exercise:
always @(*) begin
casez (in[3:0])
4'bzzz1: out = 0; // in[3:1] can be anything
4'bzz1z: out = 1;
4'bz1zz: out = 2;
4'b1zzz: out = 3;
default: out = 0;
endcase
end
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
A case statement behaves as though each item is checked sequentially (in reality, it does something more like generating a giant truth table then making gates). Notice how there are certain inputs (e.g., 4’b1111) that will match more than one case item. The first match is chosen (so 4’b1111 matches the first item, out = 0, but not any of the later ones).
- There is also a similar casex that treats both x and z as don’t-care. I don’t see much purpose to using it over casez.
- The digit ? is a synonym for z. so 2’bz0 is the same as 2’b?0
It may be less error-prone to explicitly specify the priority behaviour rather than rely on the ordering of the case items. For example, the following will still behave the same way if some of the case items were reordered, because any bit pattern can only match at most one case item:
casez (in[3:0])
4'bzzz1: ...
4'bzz10: ...
4'bz100: ...
4'b1000: ...
default: ...
endcase
- 1
- 2
- 3
- 4
- 5
- 6
- 7
your coding here:
// synthesis verilog_input_version verilog_2001 module top_module ( input [7:0] in, output reg [2:0] pos ); always @(*) begin casez (in) 8'bzzzzzzz1: pos = 0; 8'bzzzzzz10: pos = 1; 8'bzzzzz100: pos = 2; 8'bzzzz1000: pos = 3; 8'bzzz10000: pos = 4; 8'bzz100000: pos = 5; 8'bz1000000: pos = 6; 8'b10000000: pos = 7; default: pos = 0; endcase end endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
8 Always nolatches
Suppose you’re building a circuit to process scancodes from a PS/2 keyboard for a game. Given the last two bytes of scancodes received, you need to indicate whether one of the arrow keys on the keyboard have been pressed. This involves a fairly simple mapping, which can be implemented as a case statement (or if-elseif) with four cases.
| Scancode [15:0] | Arrow key |
|---|---|
16'he06b | left arrow |
16'he072 | down arrow |
16'he074 | right arrow |
16'he075 | up arrow |
| Anything else | none |
Your circuit has one 16-bit input, and four outputs. Build this circuit that recognizes these four scancodes and asserts the correct output.
To avoid creating latches, all outputs must be assigned a value in all possible conditions ( Simply having a default case is not enough. You must assign a value to all four outputs in all four cases and the default case. This can involve a lot of unnecessary typing. One easy way around this is to assign a “default value” to the outputs before the case statement:
always @(*) begin
up = 1'b0; down = 1'b0; left = 1'b0; right = 1'b0;
case (scancode)
... // Set to 1 as necessary.
endcase
end
- 1
- 2
- 3
- 4
- 5
- 6
This style of code ensures the outputs are assigned a value (of 0) in all possible cases unless the case statement overrides the assignment. This also means that a default: case item becomes unnecessary.
Reminder: The logic synthesizer generates a combinational circuit that behaves equivalently to what the code describes. Hardware does not “execute” the lines of code in sequence.
// synthesis verilog_input_version verilog_2001 module top_module ( input [15:0] scancode, output reg left, output reg down, output reg right, output reg up ); always @(*) begin up <= 1'b0; down <= 1'b0; left <= 1'b0; right <= 1'b0; case (scancode) 16'he06b: left <= 1; 16'he072: down <= 1; 16'he074: right <= 1; 16'he075: up <= 1; default: {up,down,left,right} <= 0; endcase end endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
more Verilog features
1 condition
Verilog has a ternary conditional operator ( ? : ) much like C:
(condition ? if_true : if_false)
- 1
This can be used to choose one of two values based on condition (a mux!) on one line, without using an if-then inside a combinational always block.
(0 ? 3 : 5) // This is 5 because the condition is false. (sel ? b : a) // A 2-to-1 multiplexer between a and b selected by sel. always @(posedge clk) // A T-flip-flop. q <= toggle ? ~q : q; always @(*) // State transition logic for a one-input FSM case (state) A: next = w ? B : A; B: next = w ? A : B; endcase assign out = ena ? q : 1'bz; // A tri-state buffer ((sel[1:0] == 2'h0) ? a : // A 3-to-1 mux (sel[1:0] == 2'h1) ? b : c )
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
Given four unsigned numbers, find the minimum. Unsigned numbers can be compared with standard comparison operators (a < b). Use the conditional operator to make two-way min circuits, then compose a few of them to create a 4-way min circuit. You’ll probably want some wire vectors for the intermediate results.
module top_module (
input [7:0] a, b, c, d,
output [7:0] min);//
wire [7:0] buffer1, buffer2 ;
assign buffer1 = ( a < b ) ? a : b ;
assign buffer2 = ( c < d ) ? c : d ;
assign min = (buffer1 < buffer2) ? buffer1 : buffer2 ;
endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
2 Reduction
Create a circuit that will compute a parity bit for a 8-bit byte (which will add a 9th bit to the byte). We will use “even” parity, where the parity bit is just the XOR of all 8 data bits.
module top_module (
input [7:0] in,
output parity);
assign parity = ^ in[7:0];
endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
3 Gates100
Build a combinational circuit with 100 inputs, in[99:0].
There are 3 outputs:
- out_and: output of a 100-input AND gate.
- out_or: output of a 100-input OR gate.
- out_xor: output of a 100-input XOR gate.
module top_module(
input [99:0] in,
output out_and,
output out_or,
output out_xor
);
assign out_and = & in [99:0];
assign out_or = | in[99:0];
assign out_xor = ^ in[99:0];
endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
4 Vector100r
Given a 100-bit input vector [99:0], reverse its bit ordering.
module top_module(
input [99:0] in,
output [99:0] out
);
integer i;
always @(*) begin
for ( i = 0 ; i<100 ; i++ ) begin
out[i] = in[99-i];
end
end
endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
5 Popcount255
A “population count” circuit counts the number of '1’s in an input vector. Build a population count circuit for a 255-bit input vector.
module top_module( input [254:0] in, output [7:0] out ); integer i ; always @(*) begin out = 1'b0; for ( i = 0 ; i < 255 ; i++ ) begin if ( in[i] == 1 ) begin out++; end end end endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
一种更好的写法:
module top_module(
input [254:0] in,
output [7:0] out );
integer i ;
always @(*) begin
out = 1'b0;
for ( i = 0 ; i < 255 ; i++ ) begin
out = out + in[i];
end
end
endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
6 Adder100i
Create a 100-bit binary ripple-carry adder by instantiating 100 full adders. The adder adds two 100-bit numbers and a carry-in to produce a 100-bit sum and carry out. To encourage you to actually instantiate full adders, also output the carry-out from each full adder in the ripple-carry adder. cout[99] is the final carry-out from the last full adder, and is the carry-out you usually see.
module top_module( input [99:0] a, b, input cin, output [99:0] cout, output [99:0] sum ); always @(*) begin for ( int i = 0 ; i < 100 ; i++ ) begin if (i == 0) begin cout[i] <= a[i] & b[i] | a[i] & cin | b[i] & cin; sum[i] <= a[i] ^ b[i] ^ cin; end else begin cout[i] <= a[i] & b[i] | a[i] & cout[i-1] | b[i] & cout [i-1]; sum[i] <= a[i] ^ b[i] ^ cout[i-1]; end end end endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
或者将其写成:
module top_module( input [99:0] a, b, input cin, output [99:0] cout, output [99:0] sum ); always @(*) begin for ( int i = 0 ; i < 100 ; i++ ) begin if (i == 0) begin { cout[i],sum[i] } = a[i] + b[i] + cin; end else begin { cout[i],sum[i] } = a[i] + b[i] + cout[i-1]; end end end endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
7 Bcdadd100
You are provided with a BCD one-digit adder named bcd_fadd that adds two BCD digits and carry-in, and produces a sum and carry-out.
module bcd_fadd (
input [3:0] a,
input [3:0] b,
input cin,
output cout,
output [3:0] sum );
- 1
- 2
- 3
- 4
- 5
- 6
Instantiate 100 copies of bcd_fadd to create a 100-digit BCD ripple-carry adder. Your adder should add two 100-digit BCD numbers (packed into 400-bit vectors) and a carry-in to produce a 100-digit sum and carry out.
module top_module( input [399:0] a, b, input cin, output cout, output [399:0] sum ); wire [100:0] c; assign c[0] = cin; genvar i; generate for ( i = 0; i<100 ; i++ ) begin : bcd_adder bcd_fadd bcdfai( .a(a[4*(i+1)-1:4*i]), .b(b[4*(i+1)-1:4*i]), .cin(c[i]), .cout(c[i+1]), .sum(sum[4*(i+1)-1:4*i]) ); end endgenerate assign cout = c[100]; endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26