深度学习pytorch——卷积神经网络（持续更新）

计算机如何解析图片？

在计算机的眼中，一张灰度图片，就是许多个数字组成的二维矩阵，每个数字就是此点的像素值（图-1）。在存储时，像素值通常位于[0, 255]区间，在深度学习中，像素值通常位于[0, 1]区间。

一张彩色图片，是使用三张图片叠加而成，即RGB（red green blue)（图-2）。

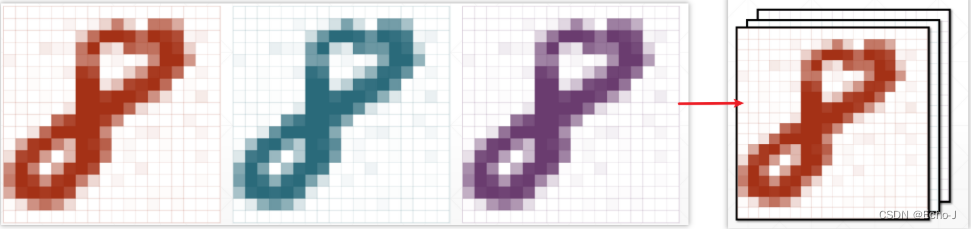
什么是卷积？

标准的神经网络是全连接的方式，全连接会获取更多的信息，但同时也包含着巨大的算力需求。在以前，算力完全不足以支撑如此巨大的计算量，但是又要进行处理，因此当时的人们联想到了人类观察事物的过程，即结合人眼观察事物的角度——先观察吸引我们的点，忽略不吸引我们的点，这称为局部相关性（Receptive Field）。应用到神经网络中，就出现了卷积的概念。

卷积操作就是先仅仅观察一部分，然后移动视野观察下一部分，这就称为卷积操作（图-3）。

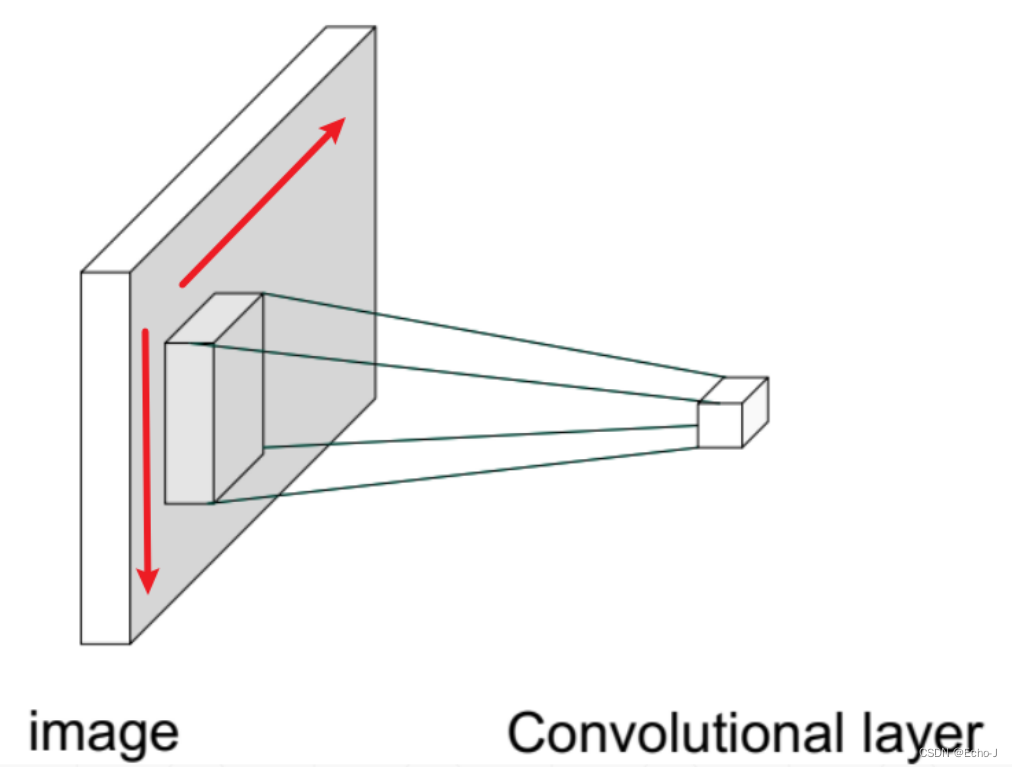
表现在神经网络中就相当于只连接局部相关性的属性（假设红色的线都是相关的，其它的都断开，当然红色的线都是我自己瞎画的），如图-4所示：

 表现在实例上就是图-5的情况：

卷积的数学表示：设x(t)为输入的数据，h(t)为遍历使用的矩阵，y(t)为经过卷积计算得到的矩阵，将x(t)和h(t)进行点乘运算，将每次点成的结果进行累加得到y(t)对应元素的值（公式-1）。 

 宏观效果（图-6）：

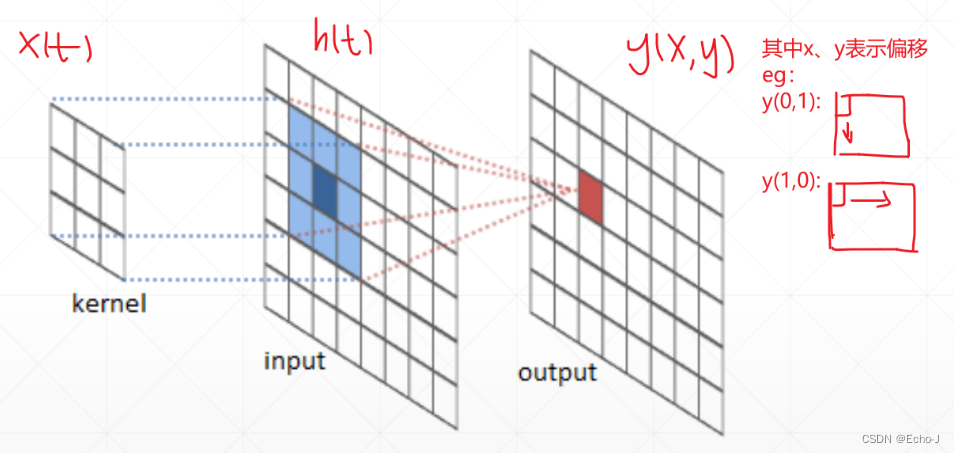
实例

以不同的 h(t) 进行卷积操作，会获取到不同的特征：

锐化（图-7）：

 模糊处理（图-8）：

 边缘检测（图-9）：

卷积神经网络

 图-3 是以1个Kernel_channel进行卷积运算。以多个Kernel_channels进行卷积运算（图-10）：

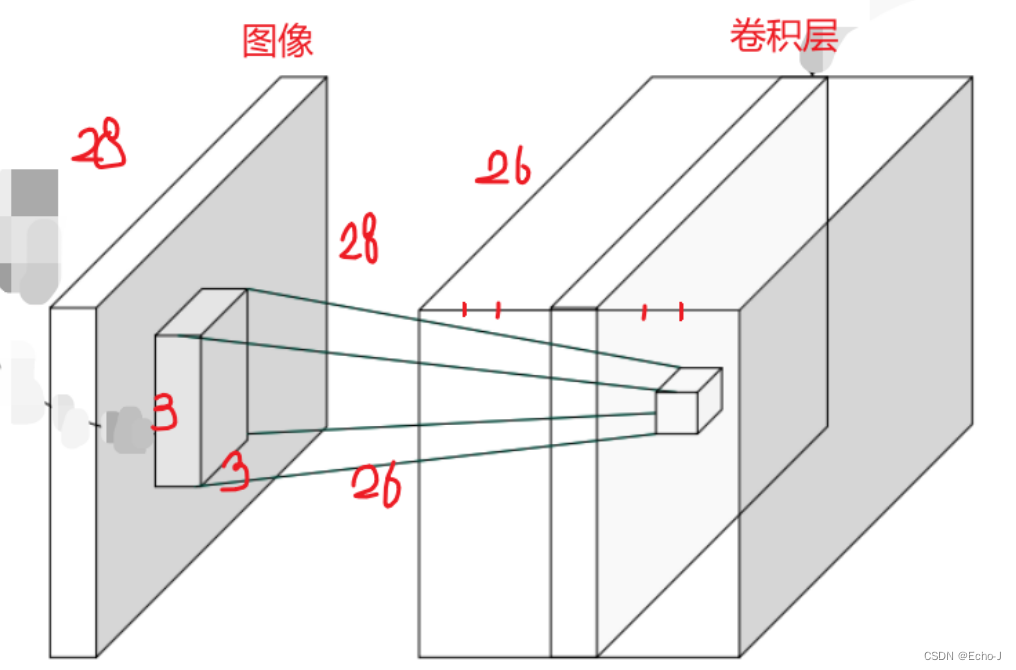
假设原来的图像是一个28*28的灰度图像，即[1, 28, 28]。使用3*3的特征矩阵以7个角度来观察这副图像，最后得到的卷积层是[7, 26, 26]。

称呼声明：

Input_channels :输入的图像的通道，彩色图像就是3，灰度图像就是1

Kernel_channels: 以多少个视角来观察图像

Kernel_size : 特征矩阵的size

Stride: 每次向下/左移动的步长

Padding: 空白的数量，补0

实例（图-11），注意右下角的标注，每个圈中的值必须相等。将同一视角不同通道得出来的矩阵进行叠加，最后会得到一个高维的特性。卷积的过程叫做特征提取。 

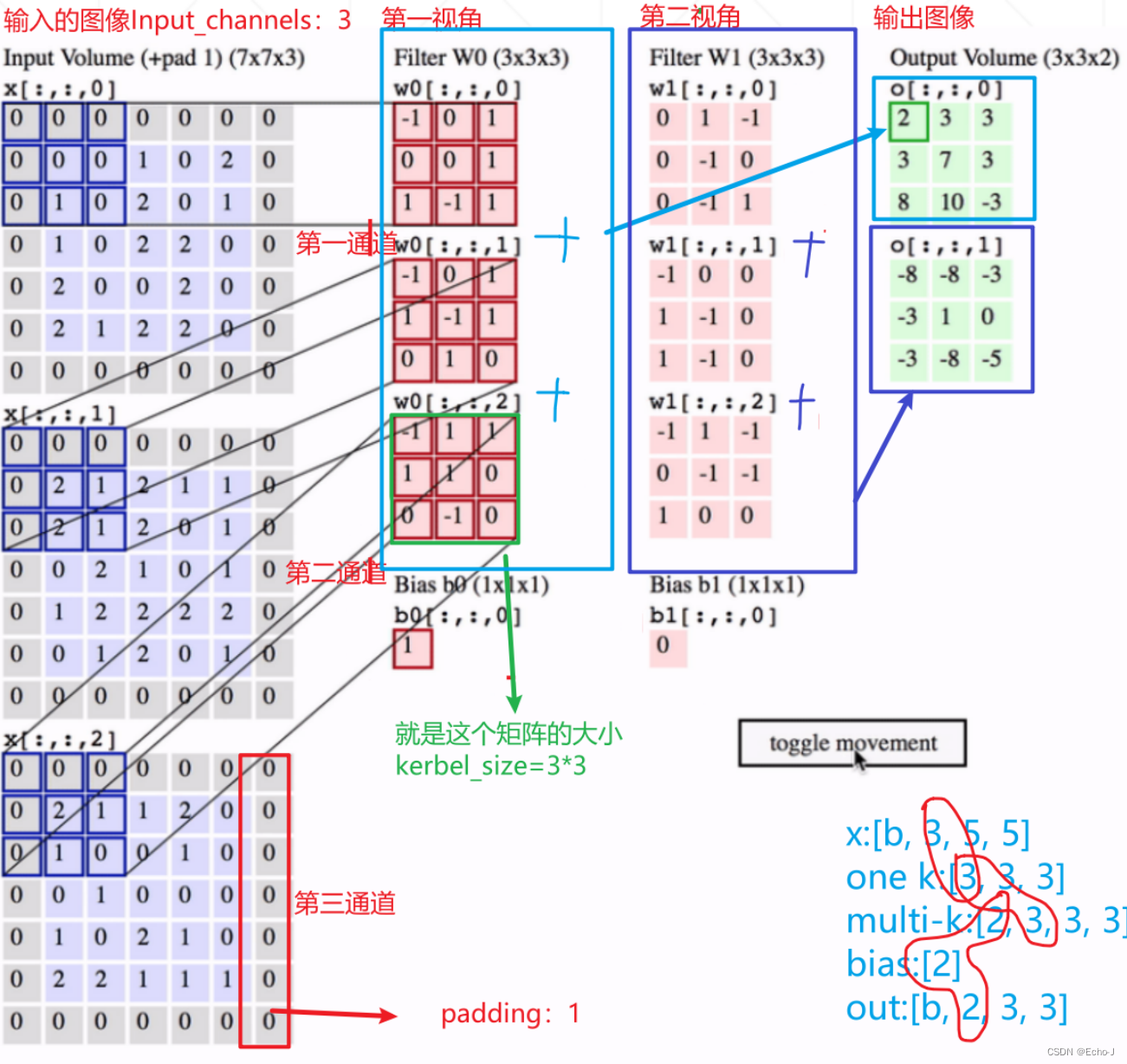
输出图像的大小计算（公式-2）：

代码示例：

# 1、
x=torch.rand(1,1,28,28)  #[b,c,h,w]
layer=nn.Conv2d(1,3,kernel_size=3,stride=1,padding=0) # weight [3,1,3,3],不补零
out=layer.forward(x)
print(out.shape)
#torch.Size([1, 3, 26, 26])
 
# 2、
layer=nn.Conv2d(1,3,kernel_size=3,stride=1,padding=1) # weight [3,1,3,3],补零
out=layer.forward(x)
print(out.shape)
#torch.Size([1, 3, 14, 14])
 
# 3、
layer=nn.Conv2d(1,3,kernel_size=3,stride=2,padding=1) # weight [3,1,3,3],补零
out=layer.forward(x)
print(out.shape)
#torch.Size([1, 3, 14, 14])
 
# 说明：
#现在基本不用layer.forward，而是用layer
out=layer(x) #推荐使用
print(out.shape)
#torch.Size([1, 3, 14, 14])
 
###### inner weight $ bias #########
#直接调用
print(layer.weight)
# Parameter containing:
# tensor([[[[-0.1249, -0.3302, -0.1774],
#           [-0.1542,  0.0873,  0.0282],
#           [-0.0006, -0.1798, -0.1030]]],
#
#
#         [[[ 0.1932,  0.3240,  0.1747],
#           [-0.2188, -0.1775, -0.0652],
#           [-0.1455, -0.1220,  0.0629]]],
#
#
#         [[[ 0.2596,  0.3017,  0.2028],
#           [-0.2629, -0.0715,  0.3267],
#           [ 0.3174, -0.1441, -0.1714]]]], requires_grad=True)
 
print(layer.weight.shape)
# torch.Size([3, 1, 3, 3])
 
print(layer.bias.shape)
# torch.Size([3])

向上/向下采样

最大采样，选取最大的（图-12）：

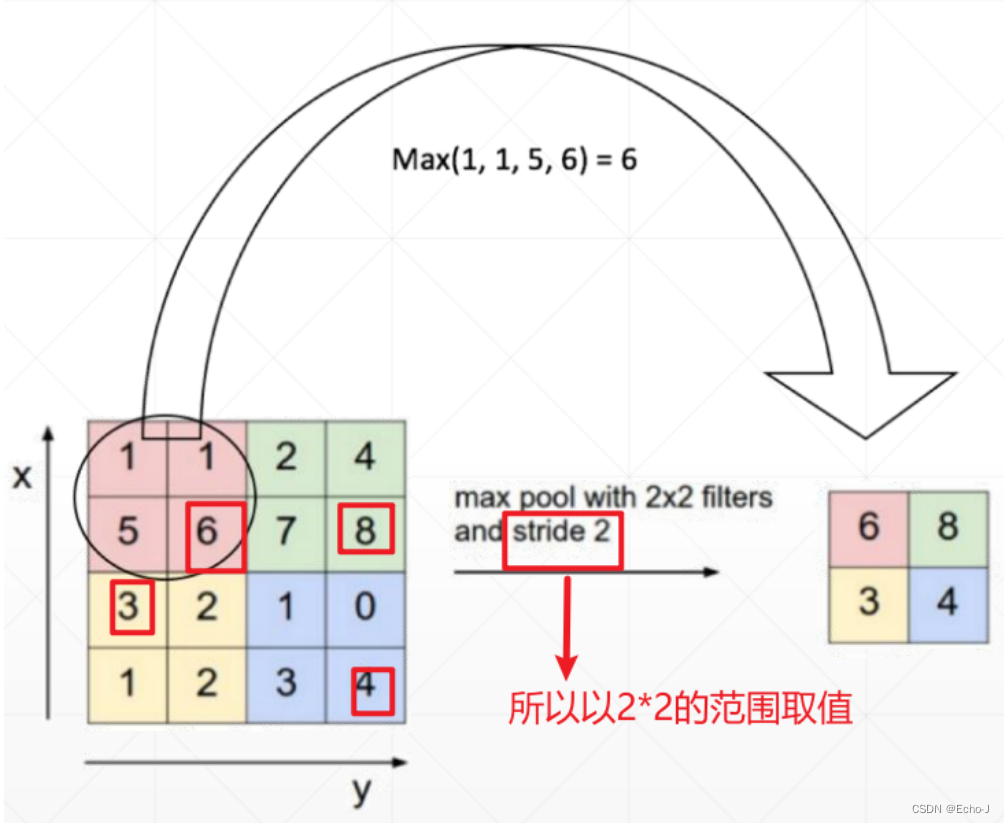
 代码演示：

x=out
print(x.shape)
#torch.Size([1, 3, 14, 14])
 
layer=nn.MaxPool2d(2,stride=2) #最大池化，2*2的滑动窗口，步长为2
out=layer(x) #推荐使用
print(out.shape)
#torch.Size([1, 3, 7, 7])

平均采样，选择平均值（图-13）：

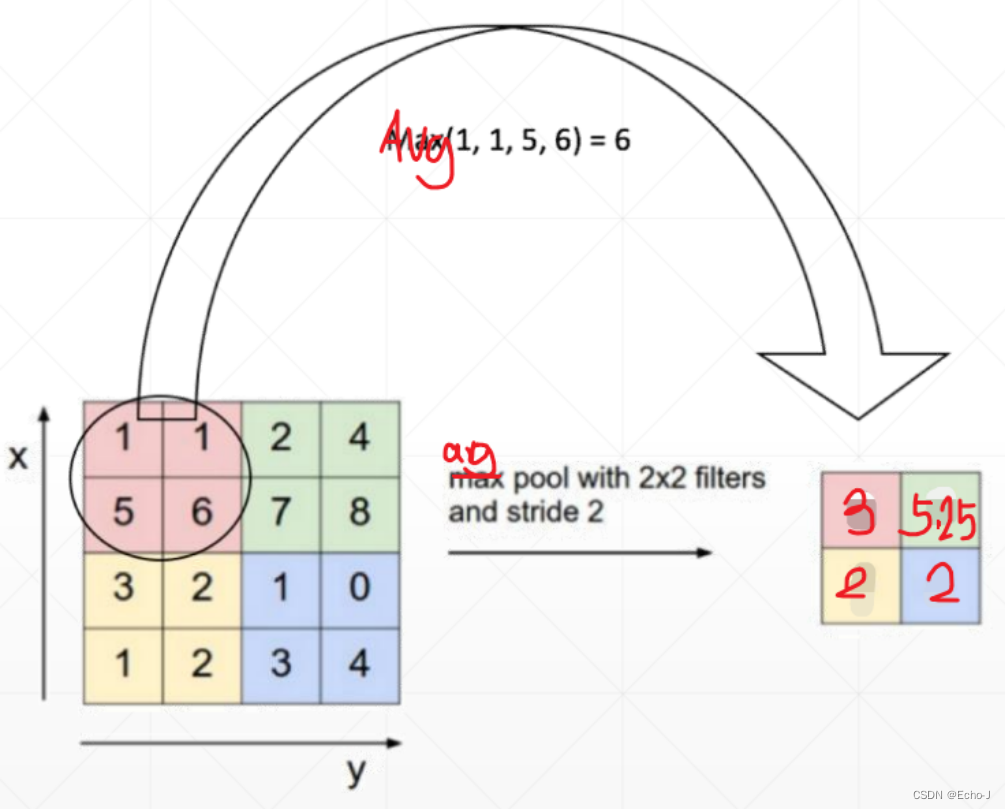
 代码演示：

x=out
print(x.shape)
#torch.Size([1, 3, 14, 14])
 
out=F.avg_pool2d(x,2,stride=2) #平均池化，2*2的滑动窗口，步长为2
print(out.shape)
#torch.Size([1, 3, 7, 7])

上采样，选取最邻近的（图-14）：

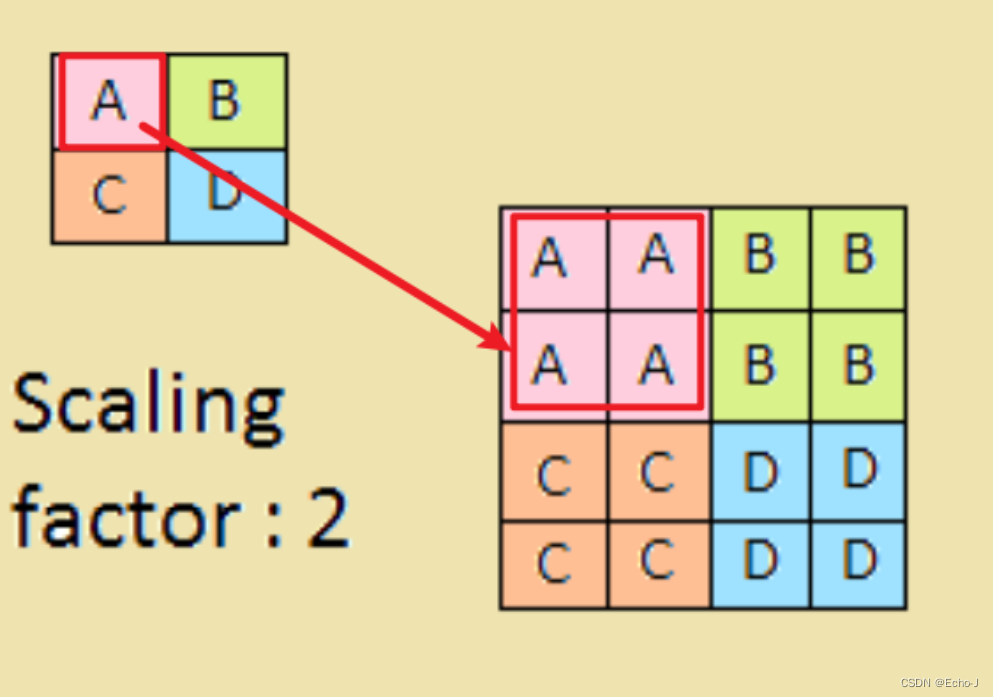
 代码演示：

x=out
print(out.shape)
# torch.Size([1, 3, 7, 7])
out=F.interpolate(x,scale_factor=2,mode='nearest')# 为放大倍数
print(out.shape) 
# torch.Size([1, 3, 14, 14])
out=F.interpolate(x,scale_factor=3,mode='nearest')
print(out.shape)
# torch.Size([1, 3, 21, 21])

 扩展到卷积层：

1、输入是一个32*32的灰度图像[1, 32, 32]，使用一个3*3的特征矩阵进行卷积，分别从6个角度进行卷积，步长为1，会得到一个[6,1,28,28]的图像
2、上采样-》[6,1,14,14]
3、卷积-》[16,1,10,10]
4、上采样-》[16,1,5,5]
5、全连接
6、全连接
7、高斯分布

ReLU

 代码演示：

#两种方式，一种是nn.ReLU，另一种是F.relu
x=out
print(x.shape)
#torch.Size([1, 3, 7, 7])
 
layer=nn.ReLU(inplace=True)
out=layer(x)
print(out.shape)
#torch.Size([1, 3, 7, 7])
 
#与上面三行等价
out=F.relu(x)
print(out.shape)
#torch.Size([1, 3, 7, 7])
 
#relu激活函数并不改变size大小