- 1日志管理系统
- 2Pygame(五)画线_pygame 画线
- 3最新目标检测论文_目标检测最新论文
- 4【小白教程】幻兽帕鲁服务器一键搭建 | 支持更新 | 自定义配置_在docker中修改帕鲁服务器设置
- 5如何来判断一个函数是否是凸函数_判断f(x1,x2)=x1^2—2x1x2+x^2+x1+x2凸函数
- 6Spring微服务实战-Spring Microservies In Action_spring microservice
- 7【统信uos-server-20-1060e】-详细安装openGauss_uos opengauss
- 8从零开始手写mmo游戏从框架到爆炸(二十一)— 战斗系统二
- 9bisect_left,bisect_right,bisect的用法,区别以源码分析_bisect_left和bisect_right区别
- 10if 语句与switch语句_分别用if语句和switch语句
转置卷积(Transposed Convolution)的介绍以及理论讲解
赞
踩
1. 转置卷积(Transposed Convolution)
论文:A guide to convolution arithmetic for deep learning
转置卷积(Transposed Convolution)也叫Fractionally-strided Convolution和Deconvolution,但用的最多的是Transposed Convolution。
Deconvolution这个名称是不建议使用的,因为该名称具有一定的误导性(和ZFNet的Deconvolution有歧义)。
1.1 注意事项
- 转置卷积不是卷积的逆运算
- 转置卷积也是一种卷积
1.2 转置卷积的目的
主要起到上采样(upsampling)的作用。
1.3 普通卷积与转置卷积的区别
1.3.1 普通卷积

下面蓝色的是卷积之前的特征图,上面绿色的是卷积之后的特征图,可以看到,普通卷积之后,特征图的大小从原来的 [ 4 , 4 ] [4, 4] [4,4] 变为了 [ 2 , 2 ] [2, 2] [2,2],整体是一个下采样的过程。
1.3.2 转置卷积

而对于这个转置卷积,输入是一个 2 × 2 2\times 2 2×2 的特征图,但是会在它的四周填充一些 0 元素,卷积核大小也是 3 × 3 3\times 3 3×3,输出是一个 4 × 4 4\times 4 4×4 的特征图。这样就实现了特征图的上采样。
需要注意的是:
- 转置卷积并不是普通卷积的逆运算
- 转置卷积本质上是上采用而非普通卷积的下采样
- 转置卷积仍然是一个卷积
2. 转置卷积的运算步骤
- 在输入特征图元素间填充 s − 1 s-1 s−1 行、列 的 0 0 0 元素
- 在输入特征图四周填充 k − p − 1 k-p-1 k−p−1 行、列的 0 0 0 元素
- 将卷积核参数上下、左右翻转
- 做正常卷积运算(步长为 1,填充为 0)—— 此时不需要再对特征图进行填充了 —— 直接进行步长为 1,padding为 0的卷积运算
其中:
- s s s 为步长
- k k k 为 kernel size
- p p p 为 padding
对于普通卷积而言,
stride=1, padding=0则特征图前后的 height 和 width 是不变的。
2.1 几个例子
2.1.1 第一个例子: s = 1 , p = 0 , k = 3 s=1, p=0, k=3 s=1,p=0,k=3

- 在输入特征图元素间填充 s − 1 = 1 − 1 = 0 s-1=1-1=0 s−1=1−1=0 行、列的 0 0 0元素 —— 不需要在特征图元素之间填充0元素
- 在输入特征图四周填充 k − p − 1 = 3 − 0 − 1 = 2 k-p-1 = 3 -0 - 1 = 2 k−p−1=3−0−1=2 行、列的 0 0 0元素 —— 在特征图四周填充2行2列的0元素
- 将卷积核参数上下、左右翻转
- 做正常卷积运算(步长为1,填充为0)—— 此时不需要再对特征图进行填充了 —— 直接进行步长为1,padding为0的卷积运算
2.1.2 第二个例子: s = 2 , p = 0 , k = 3 s=2, p=0, k=3 s=2,p=0,k=3

- 在输入特征图元素间填充 s − 1 = 2 − 1 = 1 s-1=2-1=1 s−1=2−1=1 行、列的 0 0 0元素 —— 需要在特征图元素之间填充1行和1列0元素
- 在输入特征图四周填充 k − p − 1 = 3 − 0 − 1 = 2 k-p-1 = 3-0-1=2 k−p−1=3−0−1=2 行、列的 0 0 0元素 —— 在特征图四周填充2行2列的0元素
- 将卷积核参数上下、左右翻转
- 做正常卷积运算(步长为1,填充为0)—— 此时不需要再对特征图进行填充了 —— 直接进行步长为1,padding为0的卷积运算
2.1.3 第三个例子: s = 2 , p = 1 , k = 3 s=2, p=1, k=3 s=2,p=1,k=3

- 在输入特征图元素间填充 s − 1 = 2 − 1 = 1 s-1=2-1=1 s−1=2−1=1 行、列的 0 0 0元素 —— 需要在特征图元素之间填充1行和1列0元素
- 在输入特征图四周填充 k − p − 1 = 3 − 1 − 1 = 1 k-p-1 = 3-1-1=1 k−p−1=3−1−1=1 行、列的 0 0 0元素 —— 在特征图四周填充1行1列的0元素
- 将卷积核参数上下、左右翻转
- 做正常卷积运算(步长为1,填充为0)—— 此时不需要再对特征图进行填充了 —— 直接进行步长为1,padding为0的卷积运算
2.2 输出特征图计算公式
2.2.1 普通卷积
O i c o n v / p o o l = O i i n + 2 p i − k i s i + 1 O_i^{\mathrm{conv/pool}} = \frac{O_i^{\mathrm{in}} + 2p_i - k_i}{s_i} + 1 Oiconv/pool=siOiin+2pi−ki+1
2.2.2 空洞卷积
O i d i l a t e d c o n v = O i i n + 2 p i − d i × ( k i − 1 ) s i + 1 O_i^{\mathrm{dilated \ conv}} = \frac{O_i^{\mathrm{in}} + 2p_i - d_i \times (k_i-1)}{s_i} + 1 Oidilated conv=siOiin+2pi−di×(ki−1)+1
2.2.3 转置卷积
2.2.3.1 不带空洞卷积
O i t r a n s c o n v = ( O i i n − 1 ) × s i − 2 × p i + k i O_i^{\mathrm{trans \ conv}} = (O_i^{\mathrm{in}} - 1) \times s_i - 2 \times p_i + k_i Oitrans conv=(Oiin−1)×si−2×pi+ki
2.2.3.2 带有空洞卷积
O i t r a n s c o n v = ( O i i n − 1 ) × s i − 2 × p i + d i × ( k i − 1 ) + output_padding i + 1 O_i^{\mathrm{trans \ conv}} = (O_i^{\mathrm{in}} - 1) \times s_i - 2 \times p_i + d_i \times (k_i - 1) + \text{output\_padding}_i + 1 Oitrans conv=(Oiin−1)×si−2×pi+di×(ki−1)+output_paddingi+1
2.3 实例讲解转置卷积操作
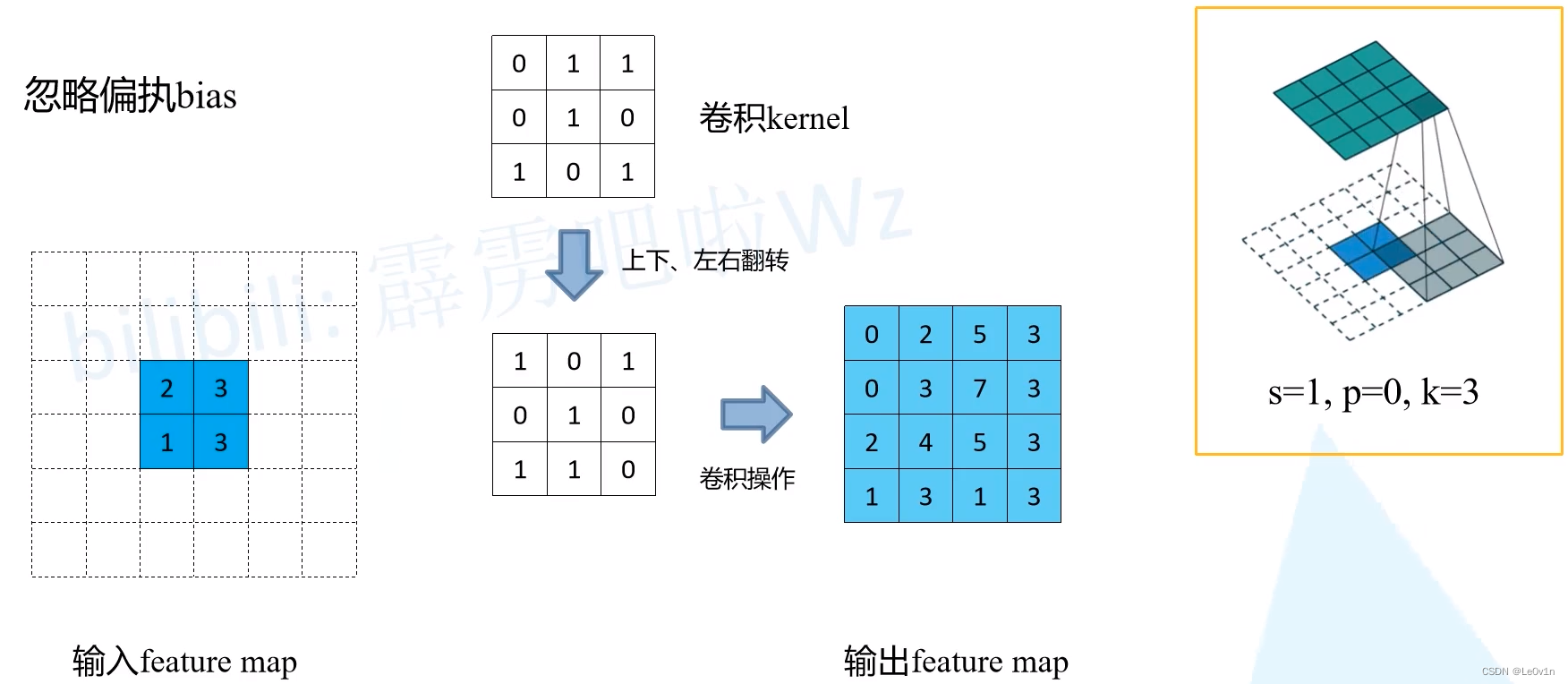
- 先根据 s , p , k s, p, k s,p,k 进行对应元素的填充
- 对 kernel 进行上下左右的翻转
- 普通卷积(stride=1, padding=0)
3. PyTorch中的转置卷积
通过在 PyTorch 官方的文档中可以看到,PyTorch 内部集成了三种转置卷积:
torch.nn.ConvTranspose1d (Python class, in ConvTranspose1d)
torch.nn.ConvTranspose2d (Python class, in ConvTranspose2d)
torch.nn.ConvTranspose3d (Python class, in ConvTranspose3d)
- 1
- 2
- 3
以torch.nn.ConvTranspose2D为例:
torch.nn.ConvTranspose2d(in_channels, out_channels,
kernel_size, stride=1, padding=0,
output_padding=0, groups=1, bias=True, dilation=1,
padding_mode='zeros', device=None, dtype=None)
- 1
- 2
- 3
- 4
在由多个输入平面组成的输入图像上应用 2D 转置卷积算子。
这个模块可以看作是 Conv2d 相对于其输入的梯度。 它也被称为分数步长卷积或反卷积(尽管它不是实际的反卷积操作,因为它不计算真正的卷积逆)。
该模块支持 TensorFloat32。
参数说明:
stridecontrols the stride for the cross-correlation.
控制互相关的步幅 对于神经网络的卷积而言,互相关就是卷积运算(和信号与处理中的定义不同,区别在于后者会对卷积核进行上下左右翻转)
这里转置卷积用的是信号与处理中卷积的操作paddingcontrols the amount of implicit zero padding on both sides for dilation × (kernel_size - 1) - padding number of points. See note below for details.
控制膨胀两边的隐式 零填充量 × (kernel_size - 1) - 填充点数。output_paddingcontrols the additional size added to one side of the output shape. See note below for details. 默认为0
控制添加到输出形状一侧的附加大小
该参数一般是不会使用的dilationcontrols the spacing between the kernel points; also known as the à trous algorithm. It is harder to describe, but the link here has a nice visualization of what dilation does.
控制内核点之间的间距;也称为 à trous 算法。很难描述,但这里的链接很好地可视化了扩张的作用 —— 就是空洞卷积的膨胀系数,默认为1(普通卷积)groupscontrols the connections between inputs and outputs. in_channels and out_channels must both be divisible bygroups.
控制输入和输出之间的连接。 in_channels 和 out_channels 都必须能被groups整除。
For example,- At groups=1, all inputs are convolved to all outputs.
所有输入都卷积到所有输出 —— 传统的卷积 - At groups=2, the operation becomes equivalent to having two conv layers side by side, each seeing half the input channels and producing half the output channels, and both subsequently concatenated.
该操作等效于并排有两个卷积层,每个卷积层看到一半的输入通道并产生一半的输出通道,并且随后将两者连接起来 —— 组卷积 - At groups=
in_channels, each input channel is convolved with its own set of filters (of size out_channels in_channels \frac{\text{out\_channels}}{\text{in\_channels}} in_channelsout_channels ). —— 深度卷积
每个输入通道都与自己的一组过滤器(大小为 out_channels in_channels \frac{\text{out\_channels}}{\text{in\_channels}} in_channelsout_channels )进行卷积
- At groups=1, all inputs are convolved to all outputs.
bias如果为True则卷积操作会有一个可学习的偏置,默认为True
4. 转置卷积和普通卷积的运算过程对比
4.1 普通卷积 —— 滑动窗口
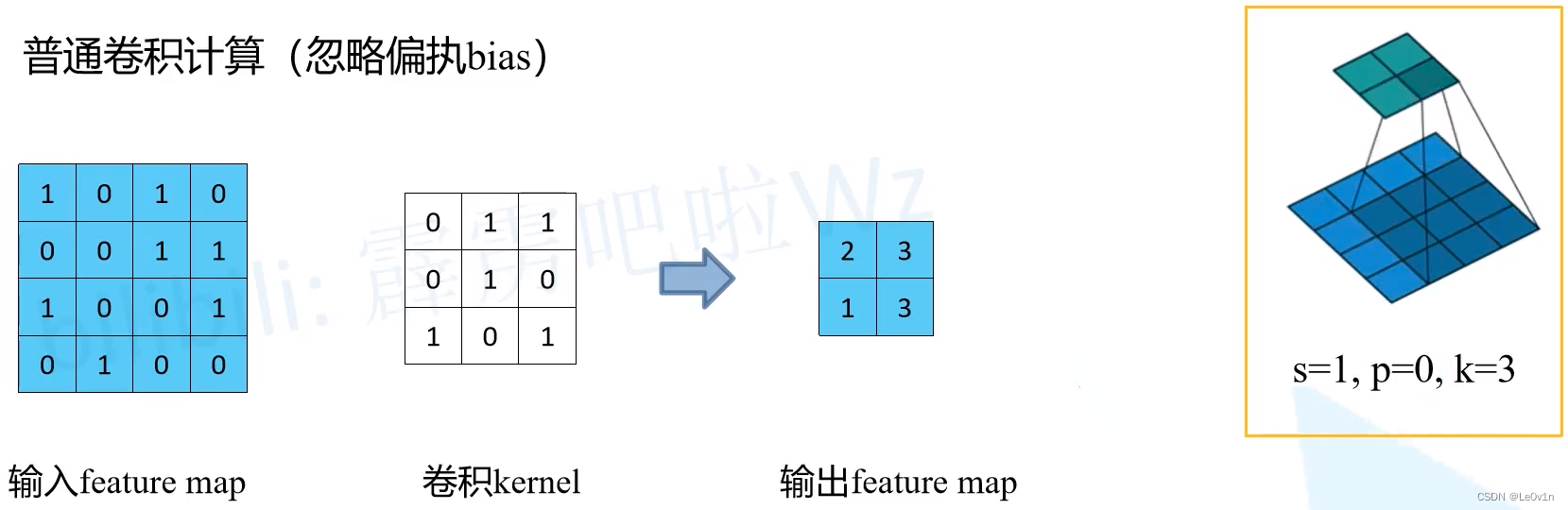
通过滑动窗口的操作得到最终2×2大小的输出特征图。
4.2 普通卷积 —— 另外一种计算方法
但在代码中真的是这样计算的吗? —— 并不是,因为这样计算效率低!更加高效的卷积操作如下:
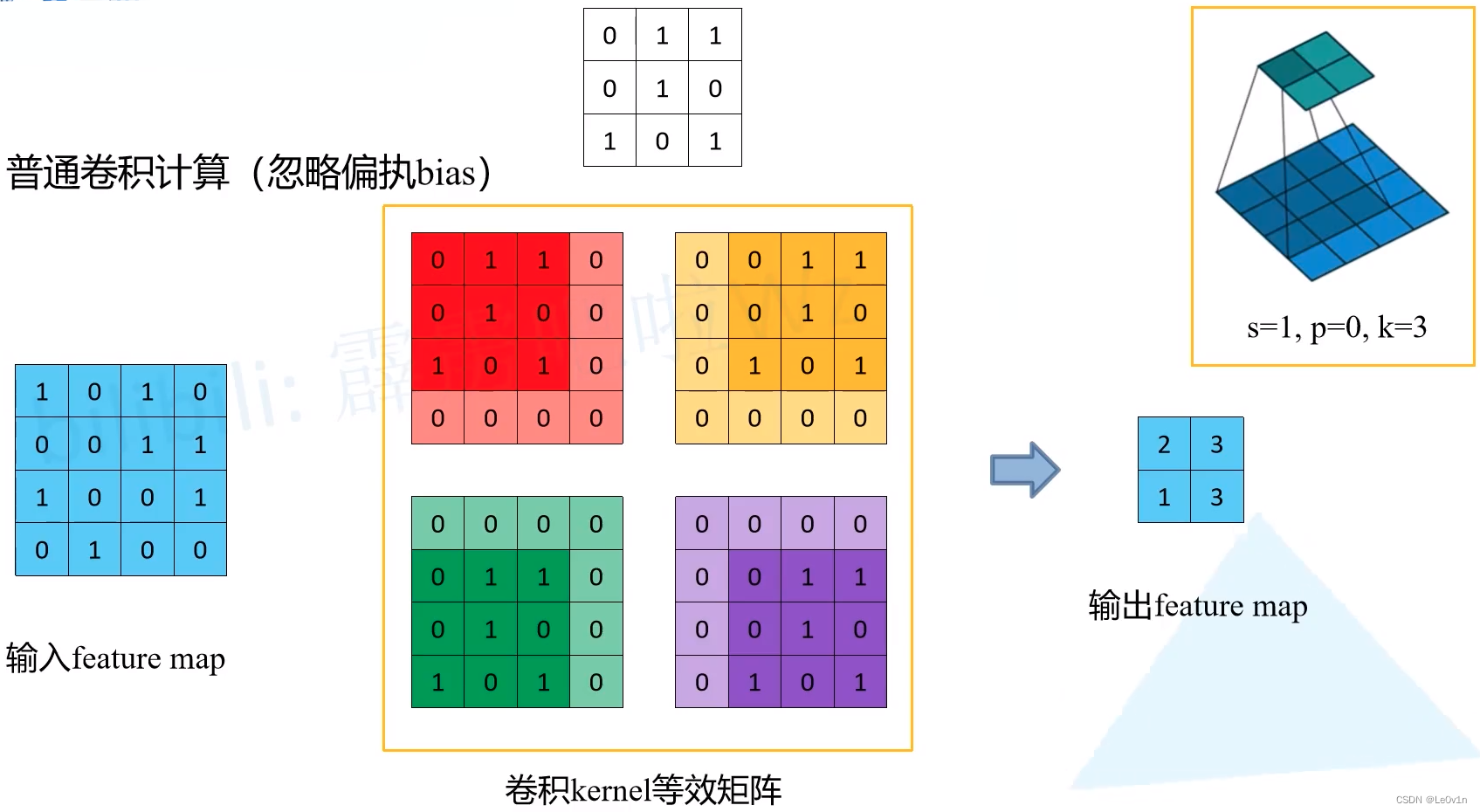
注意:对于现在版本较新的框架如TensorFlow、PyTorch而言,这种计算方法也不再采用了,有更加高效的方法代替。
- 首先需要将卷积核转化为一个个的等效矩阵,过程如下:
- 对于每一个等效矩阵,首先构建一个与输入特征图同样大小的零矩阵
- 当滑动窗口第一次运算时,将滑动窗口中值(卷积核上的值)给刚才生成的零矩阵(也就是图中有红色的矩阵)
- 当滑动窗口向右滑动时,将滑动窗口中值(卷积核上的值)给刚才生成的零矩阵(也就是图中有黄色的矩阵)
- 当滑动窗口向下滑动时,将滑动窗口中值(卷积核上的值)给刚才生成的零矩阵(也就是图中有紫色的矩阵)
- 当滑动窗口向左滑动时,将滑动窗口中值(卷积核上的值)给刚才生成的零矩阵(也就是图中有绿色的矩阵)
- 此时就可以得到这4次滑动窗口的等效矩阵(也就是4个卷积核的等效矩阵)
- 针对每一个等效矩阵,将它与输入特征图进行 ⊙ \odot ⊙和 ∑ \sum ∑,就可以得到输出特征图的每一个数值
4.3 转置卷积运算
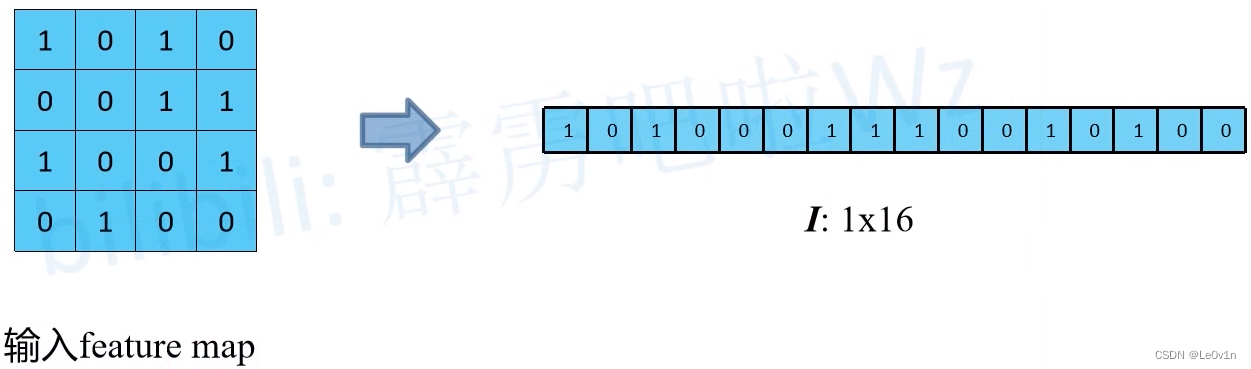
- 接下来将输入特征图进行展平,得到矩阵(向量) I ∈ R 1 × 16 I\in \mathbb{R}^{1\times 16} I∈R1×16。
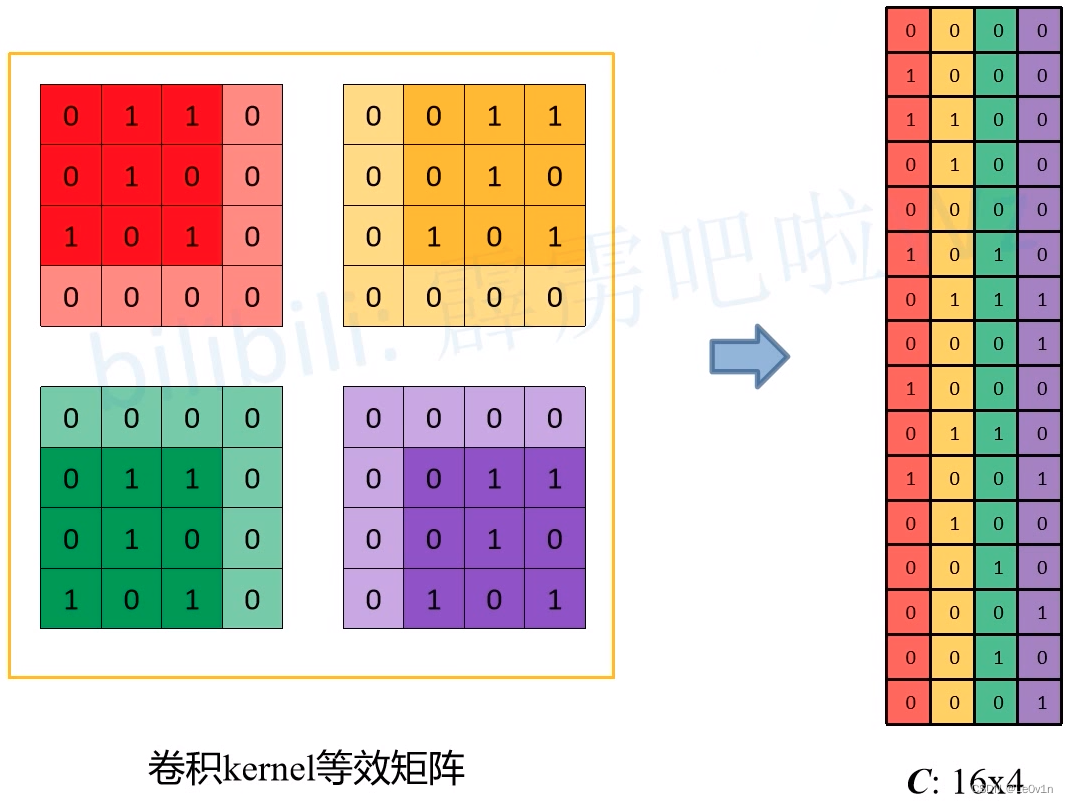
- 再将刚刚构建的4个等效矩阵进行展平,得到矩阵 C ∈ R 16 × 4 C\in \mathbb{R}^{16 \times 4} C∈R16×4。
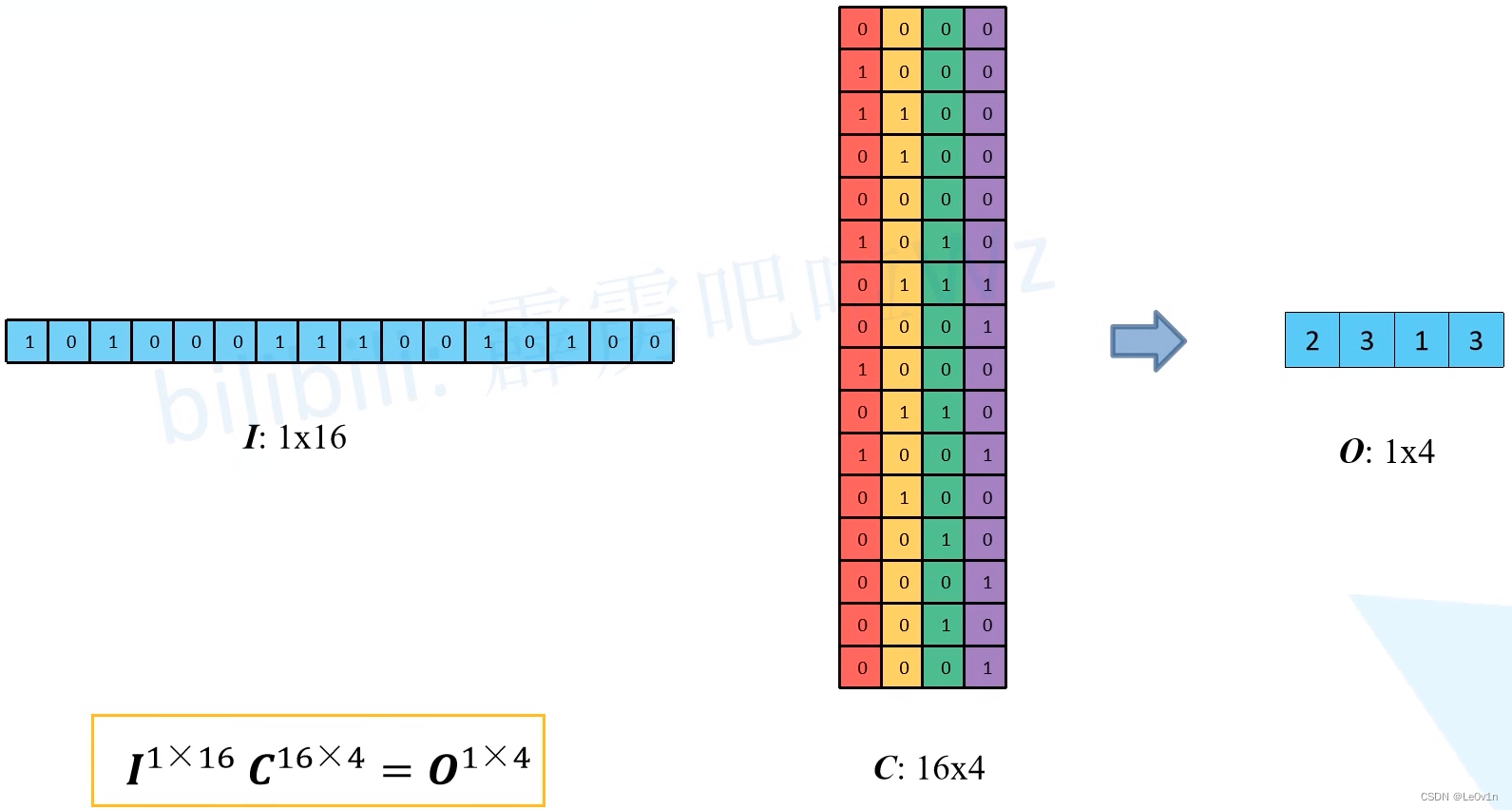
- 让矩阵
I
∈
R
1
×
16
I\in \mathbb{R}^{1\times 16}
I∈R1×16和矩阵
C
∈
R
16
×
4
C\in \mathbb{R}^{16 \times 4}
C∈R16×4进行矩阵乘法
⊗
\otimes
⊗,得到矩阵
O
∈
R
1
×
4
O\in \mathbb{R}^{1\times 4}
O∈R1×4,矩阵
O
O
O中每一个数值就是输出特征图展平之后的结果
I 1 × 16 ⊗ C 16 × 4 = O 1 × 4 I^{1\times 16} \otimes C^{16 \times 4} = O^{1\times 4} I1×16⊗C16×4=O1×4
Q:已知矩阵 C C C和矩阵 O O O,是否可以求出矩阵 I I I?换句话说:卷积是否可逆?
将矩阵两边的右侧同时乘以矩阵 C C C的逆矩阵 C − 1 ∈ R 4 × 16 C^{-1}\in \mathbb{R}^{4\times 16} C−1∈R4×16,那不就可以还原得到矩阵 I I I了吗?
—— 不可以!
A:需要注意的是,一个矩阵存在逆矩阵的条件是:它必须是一个方阵(非方阵没有逆矩阵,只有广义逆矩阵)。而这里的矩阵 C ∈ R 16 × 4 C\in \mathbb{R}^{16 \times 4} C∈R16×4,并不是一个方阵,所以它不存在逆矩阵 -> 无法还原矩阵 I I I。
一般情况下,深度学习中的卷积是不可逆的。
Q:不要求还原原始输入矩阵 I I I,只想得到与输入矩阵相同大小的矩阵 P ∈ R 1 × 16 P\in \mathbb{R}^{1\times 16} P∈R1×16,可以吗?
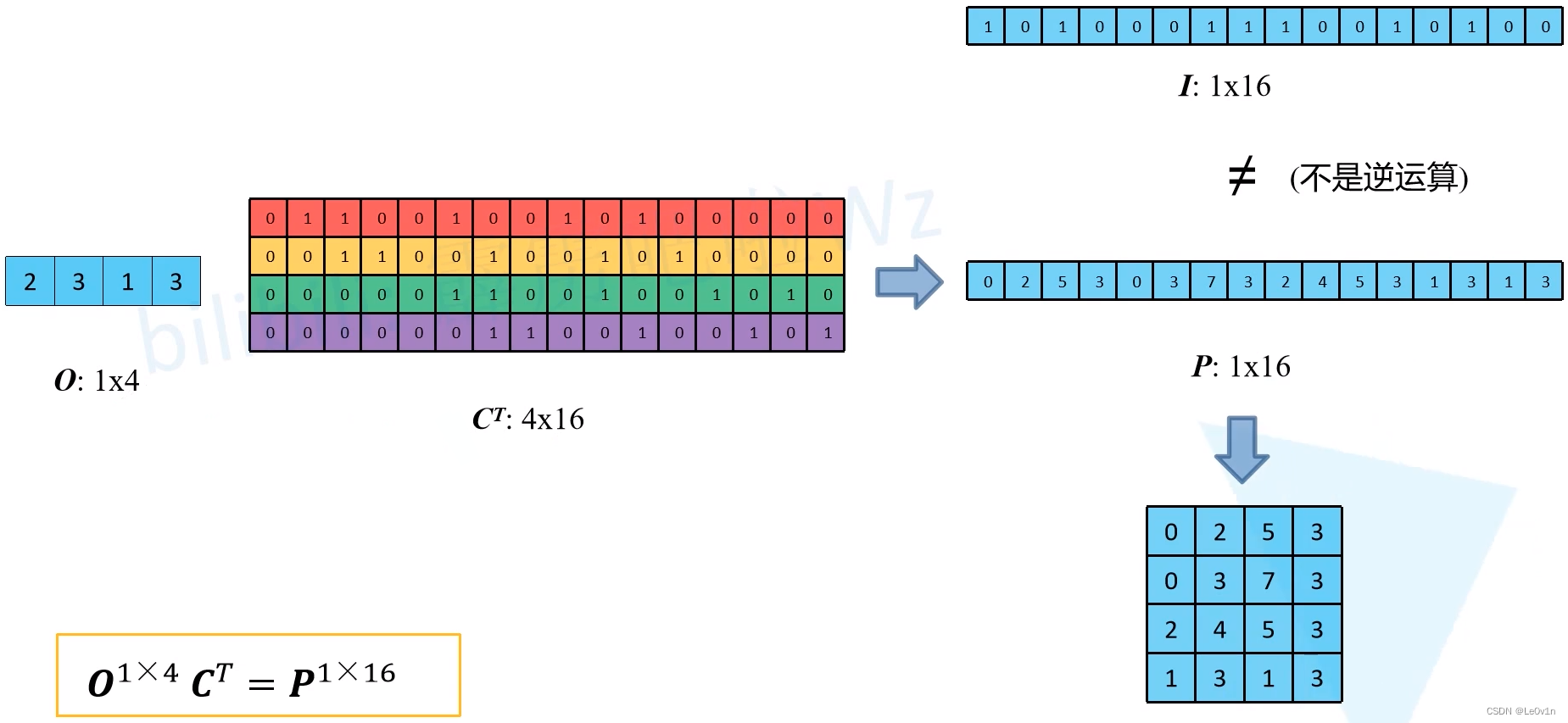
A:可以。只需要在等号两边的右侧同时乘上矩阵 C C C的转置 C T ∈ R 4 × 16 C^T\in \mathbb{R}^{4\times 16} CT∈R4×16就可以了!运算如下:
O
1
×
4
⊗
C
T
=
P
1
×
16
O^{1\times 4} \otimes C^T = P^{1\times 16}
O1×4⊗CT=P1×16
很明显,矩阵
I
I
I和矩阵
P
P
P是不相等的。
对矩阵
P
P
P进行reshape处理就得到与输入特征图shape相同的特征图。
以上就是转置卷积的运算过程,即通过一个1×4的输入特征图(其实是一个2×2的特征图),得到一个4×4的输出特征图,完成了特征图的上采样。
这也就是为什么转置卷积会被成为Deconvolution,并非空穴来风 本文内容由网友自发贡献,转载请注明出处:【wpsshop博客】
Copyright © 2003-2013 www.wpsshop.cn 版权所有,并保留所有权利。



