- 1Leetcode28. 找出字符串中第一个匹配项的下标
- 2必试!开源免费的Redis桌面管理工具:RedisInsight_redisinsight收费吗
- 3Android复习提纲_安卓应用开发复习提纲的模板
- 4安装daoker私有仓库Harbor_daokeranzhuang
- 5前端低代码平台(Vue3/React)_vue 低代码 前端
- 6从零开始制作STM32F103RCT6小车(四)_stm32f103rct6是否支持uart4
- 7three.js TextBufferGeometry创建3d文字(文字乱码问题解答)_threejs textgeometry 中文乱码
- 8高考结束后,如果你也想成为程序员,这些建议你一定要看_想当程序员
- 9RSA算法学习笔记_rsa为什么没有前向安全性
- 10云原生Docker系列 | Docker私有镜像仓库&公有镜像仓库使用_docker 阿里云镜像仓库
进入数据结构的世界_有一算法的计算次数f(n)=1000000
赞
踩
数据结构和算法的概述
一、什么是数据结构
数据结构是计算机存储、组织数据的方式。(相互之间存在一种或多种特定关系的数据元素的集合)
二、什么是算法
算法就是一系列的计算步骤,用来吧输入数据转换成输出结果。(算法就是有良好的计算过程,把一个或一组的值输入,并产出一个或一组的值输出)
三、如何去学习数据结构和算法
现在的公司对学生的代码能力越来越高,数据结构和算法的题目越来越难。算法的能力在短期内是不能够快速提升的,需要进行算法训练的积累。校招的时候,笔试很难,为了能够找到工作,还需要对数据结构和算法早早的准备,多去训练算法能力。
数据结构和算法对于初学者来说很难。但 是,古话说的好,世上无难事,只怕有心人。不管数据结构和算法有多难,我们都要硬着头皮去学。我相信,只要多学多练,学习数据结构和算法就会越来越简单。
四、算法的时间复杂度和空间复杂度
时间和空间这两个维度能够衡量算法的好坏,
4.1 算法效率
算法在编写成可执行程序后,运行程序需要耗费空间资源和时间资源。因此,衡量一个算法的好坏,一般是从时间和空间两个维度来衡量的,这就是时间复杂度和空间复杂度。
时间复杂度主要是衡量算法的运行快慢,而空间复杂度主要是衡量一个算法运行时所需要的额外空间。(计算机发展的早期,计算机存储的容量很小,我们对空间复杂度很在乎。但是经过计算机行业的快速发展,计算机存储的容量已经达到了很高的地步。所以我们今天已经不需要特别在关注算法的空间复杂度)
4.2 大O的渐进表示法
大O符号(Big O notation):用于描述函数渐进行为的数学符号
大O的渐进表示法的推导方法:
1、用常数1取代运行时间中所以的加法常数。
2、在运行次数函数中,只保留最高阶项。
3、如果最高价项存在且不是1,则去除与这个项相乘的常数,得到的结果就是大O阶。
算法的时间复杂度存在最好、平均和最坏情况:
最好情况:任意输入规模的最大运行次数(上界)
平均情况:任意输入规模的期望运行次数
最坏情况:任意输入规模的最小运行次数(下界)
例如:在一个长度为N的数组中搜索一个数据x
最好情况:1次找到
平均情况:N/2次找到
最坏情况:N次找到
实际中,我们关注的都是算法的最坏情况。所以,数组中搜索数据的时间复杂度为O(N)
4.3 时间复杂度
时间复杂度的定义:
一个算法执行所消耗的时间,从理论上说,是不能够算出来得,只有把程序放在机器上跑,才能够知道消耗的时间。一个算法所花费的时间与其中语句的执行次数成正比,算法的基本操作的执行次数,就是算法的时间复杂度。
案例1:
找到基本语句与问题规模n的数学表达式,算出该算法的时间复杂度。
//计算++count语句执行的次数 #include <stdio.h> int main() { int n = 0; scanf("%d", &n); int count = 0; for (int i = 0; i < n; i++) { for (int j = 0; j < n; j++) ++count; } for (int i = 0; i < 2 * n; i++) { ++count; } int m = 10; while (m--) { ++count; } printf("%d\n", count); return 0; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
基本操作次数:
F(n)=n^2+2*n+10
- n=10 F(n)=130
- n=100 F(n)=10210
- n=1000 F(n)=1002010
用大O的渐进表示法,时间复杂度为O(N^2)
- n=10 F(n)=100
- n=100 F(n)=10000
- n=1000 F(n)=1000000
实际中我们计算时间复杂度时,并不一定计算精准的时间复杂度,而只需要大概执行次数,这里我们使用大O的渐进表示法。
通过上面我们可以发现大O的渐进表示法去掉了那些对结果影响不大的项,简洁明了的表示出了执行次数。
案例2:
计算Fun2的时间复杂度 void Fun2() { int N; scanf("%d", &N); int count = 0; for (int i = 0; i < 2 * N; i++) { ++count; } int M = 10; while (M--) { ++count; } printf("%d\n", count); }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
Fun2的时间复杂度为:
F(N)=2*N+10
大O的渐进表示法:时间复杂度为O(N)
案例3:
//计算Fun3的时间复杂度 void Fun3() { int N, M; scanf("%d%d", &N, &M); int count = 0; for (int i = 0; i < N; i++) { ++count; } for (int j = 0; j < M; j++) { ++count; } printf("%d\n", count); }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
Fun2的时间复杂度为:
F(N)=N+M
大O的渐进表示法:时间复杂度为O(N)
案例4:
//二分查找的思想 void Fun4() { int m = 0; int arr[10] = { 1,2,4,6,8,11,55,66,77,88}; int n; printf("请输入要查找的数:\n"); scanf("%d", &n); int begin = 0; int end = 9; while (begin <= end) { int mid = begin + (end - begin)/2; if (arr[mid] < n) begin = mid + 1; else if (arr[mid] > n) end = mid - 1; else { printf("找到了\n"); printf("%d", arr[mid]); m = 1; break; } } if(m==0) printf("没找到\n"); }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
区间数据个数:
N
N/2
N/2/2
…………
N/2/2/2……/2=1
最坏的情况,查找区间缩放只剩一个值时,就是坏得,
假设查找x次,2^x=N,所以x=logN。
大O的渐进表示法:时间复杂度为O(logN).
案例5:
//斐波那契递归的复杂度 #include <stdio.h> int Fun5(size_t n) { if (n < 3) return 1; return Fun5(n - 2) + Fun5(n - 1); } int main() { int n = 7; int sum=Fun5(n); printf("%d\n", sum); return 0; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
打印结果:
递归展开图:
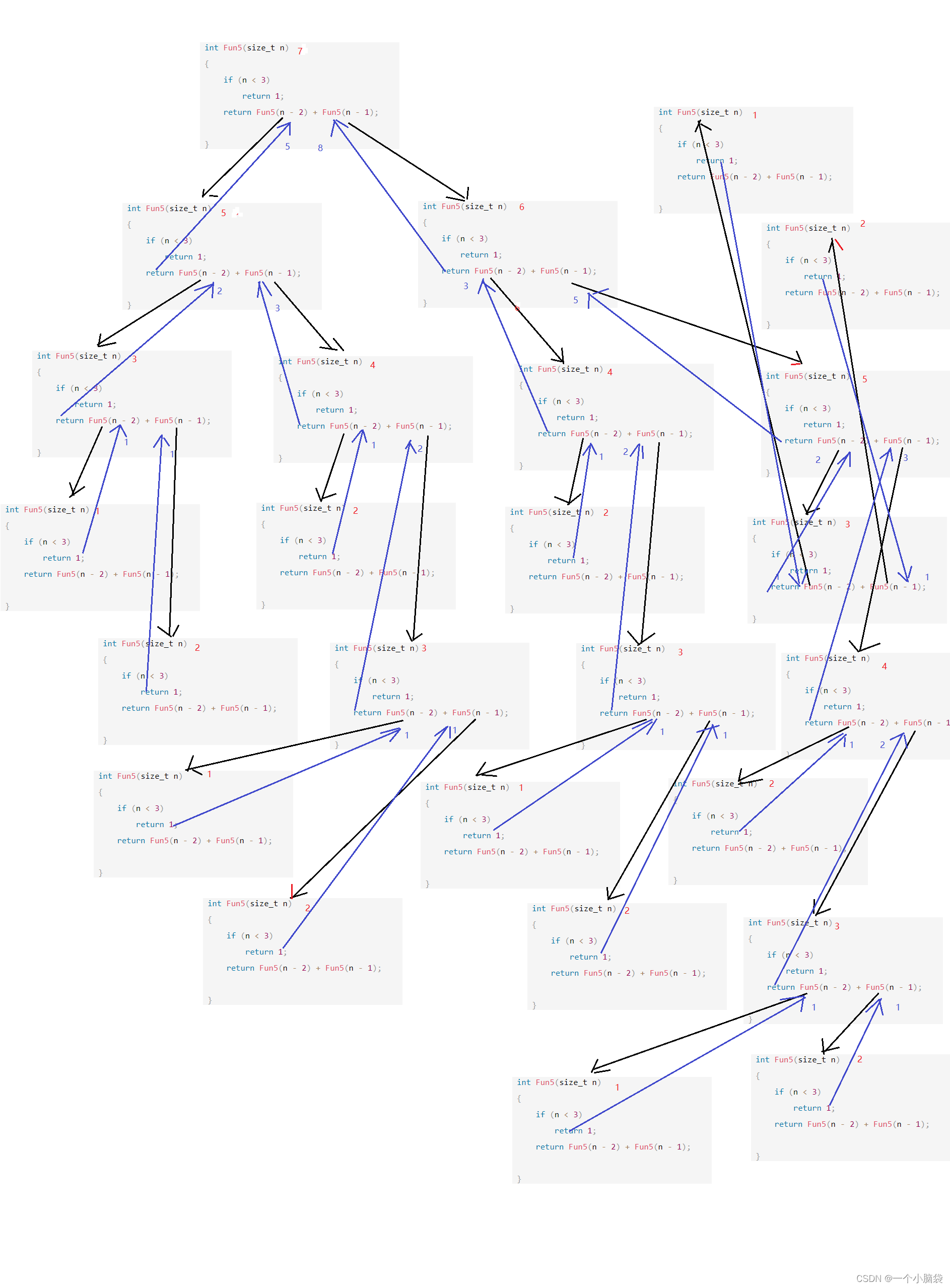
1次(2^ 0)
2次(2^ 1)
4次(2^ 2)
8次(2^ 3)
……
2^(N-1)次
通过函数递归图分析基本操作递归了2 ^N-1次,
大O的渐进表示法:时间复杂度为O (2 ^N)。
4.4 空间复杂度
空间复杂度的定义:
一个算法在运行过程中临时占用存储空间大小的量度。(空间复杂度算的是变量的个数)
注意:
函数运行时所需要的栈空间(存储函数、局部变量、一些寄存器信息等)在编译期间就已经确定好了,因此,空间复杂度主要就是函数在运行的时候申请的额外空间来确定的。
案例1:
//计算BubbleSort函数的空间复杂度 void BubbleSort(int* a, int n) { assert(a); for (int end = n; end > 0; end--) { int exchange = 0; for (int i = 1; i < n; i++) { if (a[i - 1] > a[i]) { Swap(&a[i - 1], &a[i]); exchange = 1; } } //不需要循环了 if (exchange == 0) break; } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
可以看出使用了常数个额外空间,所以空间复杂度为O(1)
案例2:
//看返回斐波那契数列的前n项,计算Fibonac的空间复杂度
int* Fibonac(int n)
{
if (n == 0)
return NULL;
int* fibar = (int*)malloc(sizeof(int) * (n + 1));
fibar[0] = 0;
fibar[1] = 1;
for (int i = 2; i <= n; i++)
{
fibar[i] = fibar[i - 1] + fibar[i - 2];
}
return fibar[i];
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
动态开辟了n+1个空间,大O的渐进表示法为O(N);
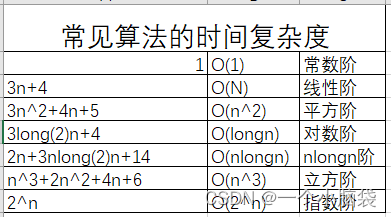
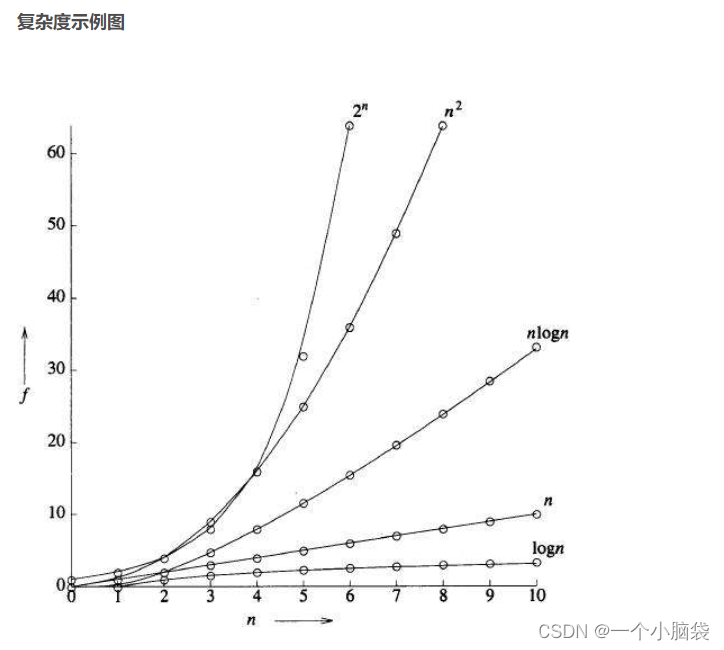
4.5 常见复杂度对比