【智能优化算法-鹅群优化算法 】基于鹅群优化算法求解单目标优化问题附matlab代码_塘鹅优化算法

 1 内容介绍

 

​在许多实际应用中，受自然启发的基于种群的搜索算法已被应用于解决数值优化问题。本文重点介绍了一种简单而强大的群优化器，名为 Wild Geese Algorithm (WGA)，用于大规模全局优化，其效率和性能已通过 IEEE CEC 2008 和 CEC 2010 高维 D 专场的大规模测试函数得到验证= 100, 500, 1000。WGA 的灵感来自自然界中的野鹅，并模拟了它们生活的各个方面，例如进化、定期合作迁徙和死亡。将 WGA 在寻找高维优化问题的全局最优解方面的有效性与之前文献中报道的其他方法进行了比较。实验结果表明，所提出的 WGA 在解决一系列大规模优化问题方面具有高效的性能，尽管其结构更简单、实现更容易，但在其他大规模优化算法中具有很强的竞争力。

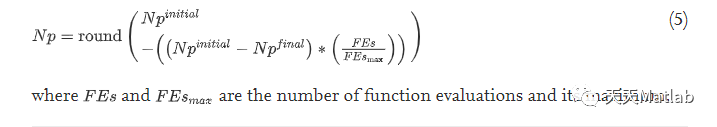
2 仿真代码

clc
clear
close all
% M. Ghasemi, A. Rahimnejad, R. Hemmati, E. Akbari, and S. A. Gadsden,
% 揥ild Geese Algorithm: A novel algorithm for large scale optimization
% based on the natural life and death of wild geese,? 
% Array, vol. 11, p. 100074, Sep. 2021, 
% doi: 10.1016/J.ARRAY.2021.100074.
% WebLink to Full Text Article: https://doi.org/10.1016/J.ARRAY.2021.100074

disp('Wild Geese Algorithm');

nPop=120;
nVar=1000;
nPop_Initial=nPop;
nPop_Final=30;

MaxNFE=20000;
MaxIter0=ceil(MaxNFE/((nPop_Initial+nPop_Final)/2));   % Approximate Maximum Iterations

Cr=0.5;

xmin=-600;
xmax=-xmin;

%%%%%%%%%%%

NFE=0;
Gbest.Position=[];
Gbest.Cost=inf;
BestCosts=nan(1,MaxIter0);
nfe=BestCosts;

for i=1:nPop
    Velocity(i,:)=zeros(1,nVar); %#ok<*SAGROW>
    Position(i,:)=xmin+(xmax-xmin)*rand(1,nVar);
    Cost(i)=CostFunction(Position(i,:));
    PbestPosition(i,:)=Position(i,:);
    PbestCost(i)=Cost(i);
    PbestVel(i,:)=Velocity(i,:);
    
    if PbestCost(i)<Gbest.Cost
        Gbest.Position=PbestPosition(i,:);
        Gbest.Cost=PbestCost(i);
        Gbest.Velocity= PbestVel(i,:);
    end
end
NFE=NFE+nPop;

iter=0;
while NFE<=MaxNFE
    iter=iter+1;
    
    [hh, gg]=sort(PbestCost);
    
    nPop=(nPop_Initial-1)-((nPop_Initial-nPop_Final)*(NFE/MaxNFE));
    nPop=round(nPop+1);
    nPop=max(nPop,nPop_Final);
    nPop=min(nPop_Initial,nPop);
    B6=nPop_Initial-nPop_Final;
    
    for eee=1:nPop
        
        if B6==0
            i=eee;
        else
            i=gg(eee);
        end
        [~, f2]=find(gg==i);
        
        %%% Worst
        if f2==nPop
            f2=0;
        end
        jj1=gg(1,f2+1);
        
        %%% BETTER
        [~, f2]=find(gg==i);
        tt=1;
        if f2==1
            f2=nPop+1;
            tt=-1;
        end
        
        jj2=gg(1,f2-1);
        if f2==2
            f2=nPop+2;
        end
        
        jj3=gg(1,f2-2);
        jjj=gg(1,1);
        ff1=gg(1,end);
        
        Velocity(i,:)= (rand(1,nVar).*Velocity(i,:)+rand(1,nVar).*(Velocity(jj2,:)-Velocity(jj1,:)))+rand(1,nVar).*(PbestPosition(i,:)-Position(jj1,:))+rand(1,nVar).*(PbestPosition(jj2,:)-Position(i,:))-rand(1,nVar).*(PbestPosition(jj1,:)-Position(jj3,:))+rand(1,nVar).*(PbestPosition(jj3,:)-Position(jj2,:));%%ORIGINAL
        
        BB=(PbestCost(jj2))/(PbestCost(i));
        GG=(PbestCost(jjj))/(PbestCost(i));
        
        Position(i,:)=PbestPosition(i,:)+rand(1,nVar).*rand(1,nVar).*(( PbestPosition(jj2,:)+Gbest.Position-2*PbestPosition(i,:))+(Velocity(i,:)));
        
        f1=(Gbest.Cost)/(PbestCost(i)+Gbest.Cost);
        f0=(PbestCost(jj2))/(PbestCost(jj2)+PbestCost(i));
        
        DE1=((PbestPosition(jj2,:)-PbestPosition(i,:)));
        
        for ww=1:nVar
            if rand<Cr
                Position(i,ww)=PbestPosition(i,ww)+rand*rand*(DE1(ww));
            end
        end
        
        Position(i,:)=min(max(Position(i,:),xmin),xmax);
        
        Cost(i)=CostFunction(Position(i,:));
        
        if Cost(i)<PbestCost(i)
            PbestPosition(i,:)=Position(i,:);
            PbestCost(i)=Cost(i);
            PbestVel(i,:)=Velocity(i,:);
            
            if PbestCost(i)<Gbest.Cost
                Gbest.Position=PbestPosition(i,:);
                Gbest.Cost=PbestCost(i);
                Gbest.Velocity= PbestVel(i,:);
            end
        end
    end
    
    NFE=NFE+nPop;
    nfe(iter)=NFE;
    BestCosts(iter)=Gbest.Cost;
    
    disp(['NFE ' num2str(NFE) ':   Best Cost = ' num2str(Gbest.Cost)]);

end
BestCosts(iter+1:end)=[];

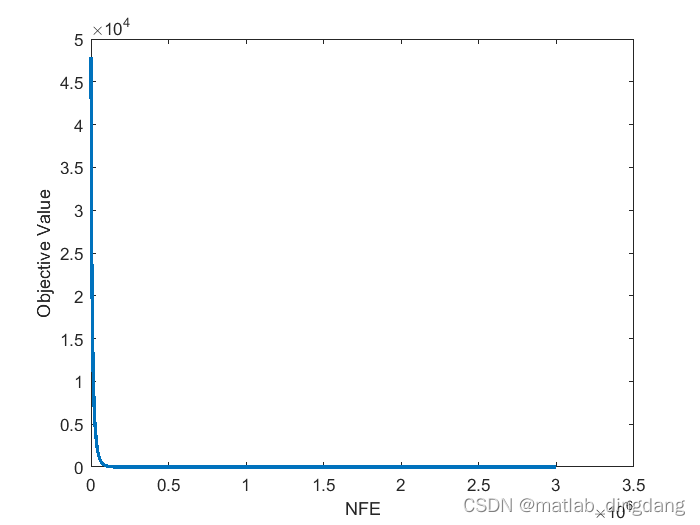
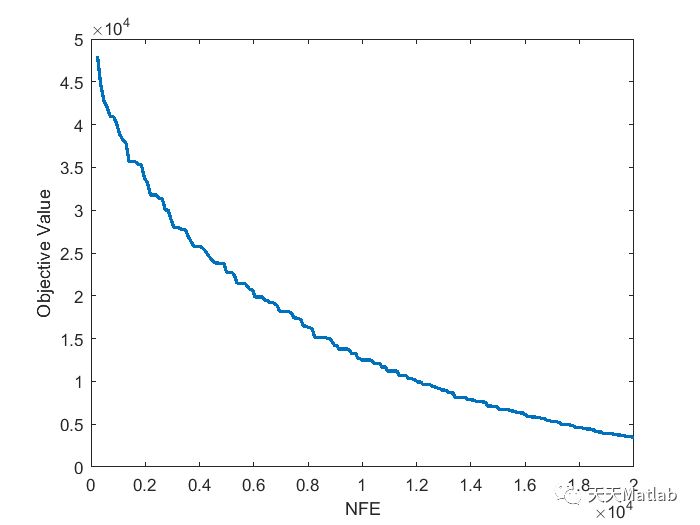
plot(nfe,BestCosts, 'LineWidth',2)
xlabel('NFE')
ylabel('Objective Value')

% o=k(1:Di);
% % z=sum((x-o).^2,2);
% x=x-repmat(o,ps,1);
% z=sum(x.^2,2);

%% F2
%  %%%%%F2%%%Schwefel-shift function)
%  o=
% o=o(1,1:Di);
% x=x-repmat(o,ps,1);
% z=sum(x.^2,2);
% z=20-20.*exp(-0.2.*sqrt(z./D))-exp(sum(cos(2.*pi.*x),2)./D)+exp(1);

%% F7
% %   7. FastFractal "DoubleDip"
% % function f=fastfractal_doubledip(x)
% % global initial_flag
% persistent o ff
% [ps,D]=size(x);
% if initial_flag==0
% o=[1];
%     load fastfractal_doubledip_data
%     ff = FastFractal('DoubleDip', 3, 1, o, D);
%     initial_flag=1;
% % end
% ff;
% z=ff.evaluate(x);
%%%%&&&&
end
% % % % % % % % % %% % % % % % % % % % % % % % % % % % % % % % % % %   % % % % % % % % % % % % % % % % % % % %   % % % % %   HH=gg(1,1:npop);% % % % %     Br=sort(HH);
 

3 运行结果

4 参考文献

[1] Ghasemi M ,  Rahimnejad A ,  Hemmati R , et al. Wild Geese Algorithm: A novel algorithm for large scale optimization based on the natural life and death of wild geese[J]. Array, 2021, 11.

博主简介：擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真，相关matlab代码问题可私信交流。

部分理论引用网络文献，若有侵权联系博主删除。