AVL树的四种不同情况的对应调整方式_avl树的所有调整情况

AVL是自平衡二叉搜索树，满足两个条件，第一个条件是：本身是二叉搜索树；第二个条件是，所有结点的左右子树高度差不超过1。

以下内容转载别处

2.平衡二叉树（AVL Tree）
2.1 什么是AVL Tree

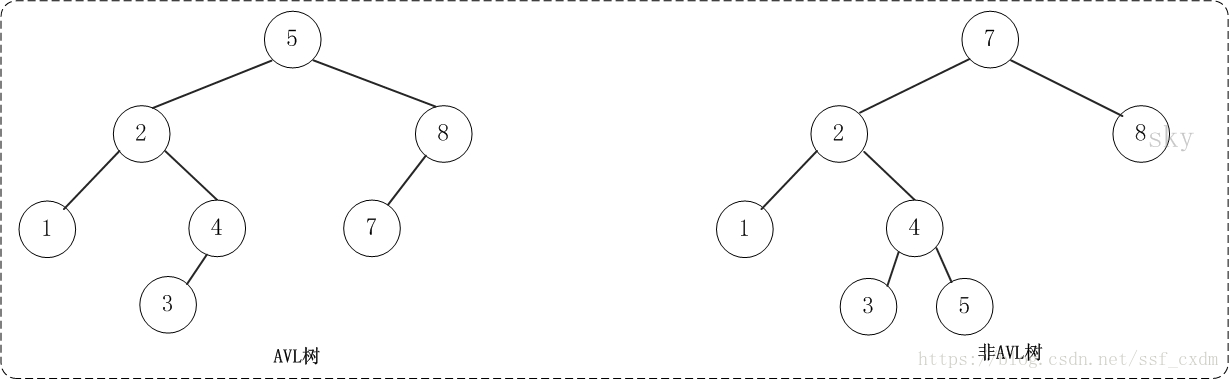
平衡二叉树（AVL树）在符合二叉查找树的条件下，还满足任何节点的两个子树的高度最大差为1。下面的两张图片，左边是AVL树，它的任何节点的两个子树的高度差<=1；右边的不是AVL树，其根节点的左子树高度为3，而右子树高度为1；

2.2 平衡二叉树的4种失衡状态

如果在AVL树中进行插入或删除节点，可能导致AVL树失去平衡，这种失去平衡的二叉树可以概括为四种姿态：LL（左左）、RR（右右）、LR（左右）、RL（右左）。它们的示意图如下：

这四种失去平衡的姿态都有各自的定义：
LL：LeftLeft，也称“左左”。插入或删除一个节点后，根节点的左孩子（Left Child）的左孩子（Left Child）还有非空节点，导致根节点的左子树高度比右子树高度高2，AVL树失去平衡。

RR：RightRight，也称“右右”。插入或删除一个节点后，根节点的右孩子（Right Child）的右孩子（Right Child）还有非空节点，导致根节点的右子树高度比左子树高度高2，AVL树失去平衡。

LR：LeftRight，也称“左右”。插入或删除一个节点后，根节点的左孩子（Left Child）的右孩子（Right Child）还有非空节点，导致根节点的左子树高度比右子树高度高2，AVL树失去平衡。

RL：RightLeft，也称“右左”。插入或删除一个节点后，根节点的右孩子（Right Child）的左孩子（Left Child）还有非空节点，导致根节点的右子树高度比左子树高度高2，AVL树失去平衡。

2.3 失衡状态 —- > 平衡状态

AVL树失去平衡之后，可以通过旋转使其恢复平衡。下面分别介绍四种失去平衡的情况下对应的旋转方法。

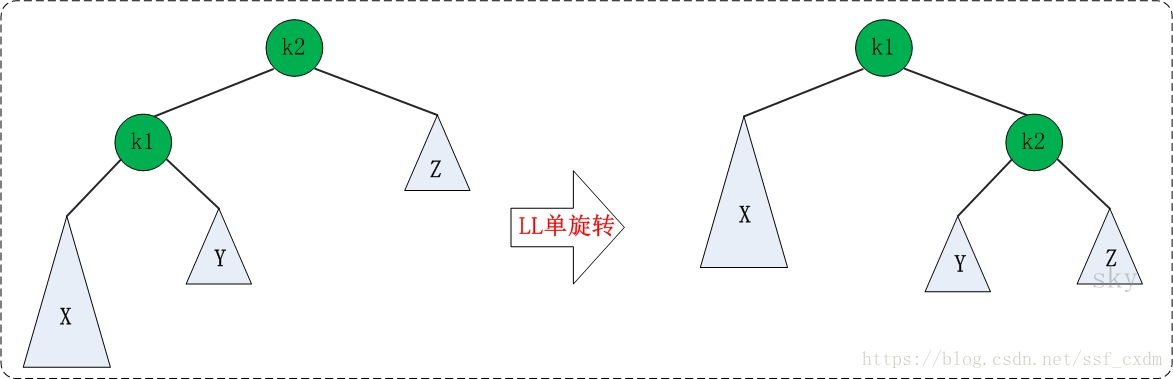
LL的旋转。LL失去平衡的情况下，可以通过一次旋转让AVL树恢复平衡。步骤如下：

1、将根节点的左孩子作为新根节点。
2、将新根节点的右孩子作为原根节点的左孩子。
3、将原根节点作为新根节点的右孩子。
LL旋转示意图如下：

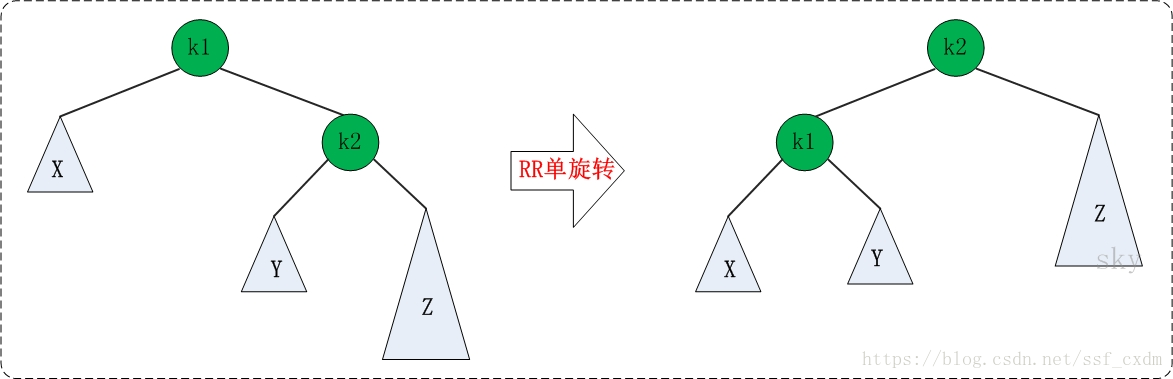
RR的旋转：RR失去平衡的情况下，旋转方法与LL旋转对称，步骤如下：

1、将根节点的右孩子作为新根节点。
2、将新根节点的左孩子作为原根节点的右孩子。
3、将原根节点作为新根节点的左孩子。
RR旋转示意图如下：

LR的旋转：LR失去平衡的情况下，需要进行两次旋转，步骤如下：

1、围绕根节点的左孩子进行RR旋转。
2、围绕根节点进行LL旋转。
LR的旋转示意图如下：

RL的旋转：RL失去平衡的情况下也需要进行两次旋转，旋转方法与LR旋转对称，步骤如下：

1、围绕根节点的右孩子进行LL旋转。
2、围绕根节点进行RR旋转。
RL的旋转示意图如下：

以下内容原创

#include<iostream>
#include<cstdlib>
using namespace std;

typedef int ElementType;
typedef struct AVLNode *Position;
typedef Position AVLTree; /* AVL树类型 */
struct AVLNode {
    ElementType Data; /* 结点数据 */
    AVLTree Left;     /* 指向左子树 */
    AVLTree Right;    /* 指向右子树 */
    int Height;       /* 树高 */
};


AVLTree SingleLeftRotation(AVLTree A)
{ /* 注意：A必须有一个左子结点B */
  /* 将A与B做左单旋，更新A与B的高度，返回新的根结点B */

    AVLTree B = A->Left;
    A->Left = B->Right;
    B->Right = A;
    A->Height = Max(GetHeight(A->Left), GetHeight(A->Right)) + 1;
    B->Height = Max(GetHeight(B->Left), A->Height) + 1;

    return B;
}
AVLTree SingleRightRotation(AVLTree A)
{
    AVLTree B = A->Right;
    A->Right = B->Left;
    B->Left = A;
    A->Height = Max(GetHeight(A->Left), GetHeight(A->Right)) + 1;
    B->Height = Max(GetHeight(B->Left), A->Height) + 1;
    return B;
}
AVLTree DoubleLeftRightRotation(AVLTree A)
{ /* 注意：A必须有一个左子结点B，且B必须有一个右子结点C */
  /* 将A、B与C做两次单旋，返回新的根结点C */

  /* 将B与C做右单旋，C被返回 */
    A->Left = SingleRightRotation(A->Left);
    /* 将A与C做左单旋，C被返回 */
    return SingleLeftRotation(A);
}
AVLTree DoubleRightLeftRotation(AVLTree A)
{
    /*将A，B与C做两次单旋，返回新的根结点C*/
    /*B与C做左单旋，C被返回*/
    A->Right = SingleLeftRotation(A->Right);
    /*将A与C做右单旋，C被返回*/
    return SingleRightRotation(A);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53