自然语言处理3——玩转文本分类 - Python NLP高级应用_python 文本分类

写在开头

随着信息时代的不断发展，海量的文本数据成为我们获取知识和信息的重要来源。如何高效地从这些文本中提取有用的信息，成为数据分析和数据挖掘领域的热门问题之一。本文将介绍文本分类在自然语言处理（NLP）中的高级应用，通过Python实现，让你轻松玩转文本分类。

1. 文本分类的背后原理和应用场景

文本分类是一种将文本数据划分为不同类别或标签的自然语言处理任务。其背后原理主要基于统计学和机器学习技术，目标是通过对文本的学习，建立一个能够自动将新文本分类到合适类别的模型。下面详细展开文本分类的原理和应用场景：

1.1 文本分类的原理

在文本分类的原理中，最常用的方法之一是朴素贝叶斯分类器。该分类器基于贝叶斯定理，通过统计文本中每个词语在不同类别中出现的概率来进行分类。朴素贝叶斯假设各个词汇之间相互独立，从而简化了计算过程。

另一种常见的方法是支持向量机（SVM），它通过在高维空间中找到一个超平面，将不同类别的文本分隔开。支持向量机适用于处理高维数据，尤其在文本分类中，文本往往可以表示为高维的词向量。

近年来，深度学习技术也在文本分类中取得了显著的成就。卷积神经网络（CNN）和循环神经网络（RNN）等模型能够学习文本中的层级特征和上下文信息，进一步提高了文本分类的准确性。

1.2 文本分类的应用场景

• 搜索引擎优化： 搜索引擎利用文本分类技术为用户提供准确的搜索结果。通过分析用户的搜索关键词，搜索引擎可以将搜索结果划分为不同的类别，提高搜索结果的相关性。

• 垃圾邮件过滤： 文本分类在垃圾邮件过滤中起到关键作用。通过对邮件文本进行分类，系统可以自动过滤掉垃圾邮件，确保用户收到的邮件更加清晰和有序。

• 情感分析： 情感分析是文本分类的一个重要应用领域，它能够分析文本中的情感倾向，判断文本是正面的、负面的还是中性的。在社交媒体、产品评论等领域，情感分析对于了解用户反馈具有重要价值。

• 新闻分类： 自动将新闻按照主题分类是文本分类的另一个应用场景。这有助于媒体组织和用户更轻松地找到感兴趣的新闻，提高信息检索的效率。

• 法律文件分类： 在法律领域，文本分类可用于对法律文件进行分类和整理，提高法律研究和文档管理的效率。

• 医学文本分类： 在医学领域，文本分类可以用于对医学文献、病历等进行分类，帮助医生更好地理解和利用医学信息。

总体而言，文本分类技术在各个领域都有着广泛的应用，为处理大量文本信息提供了自动化和智能化的解决方案。

2. 使用机器学习模型进行文本分类（朴素贝叶斯、支持向量机等）

在文本分类中，机器学习模型是实现任务的关键。我们将深入介绍两个常用的机器学习模型：朴素贝叶斯和支持向量机（SVM）。

2.1 朴素贝叶斯

朴素贝叶斯（Naive Bayes）是一种基于贝叶斯定理的统计分类算法，它是一类简单但效果良好的分类算法之一。朴素贝叶斯的“朴素”一词来源于算法对于特征之间条件独立性的假设，即每个特征在给定类别下都是独立的，这个假设有时候在实际应用中并不成立，但在实践中通常仍然能够取得较好的分类效果。

2.1.1 基本原理

朴素贝叶斯算法基于贝叶斯定理，其核心思想是通过观察先验概率和样本数据，计算后验概率，然后选择具有最大后验概率的类别作为最终的分类结果。

2.1.2 数学公式

朴素贝叶斯分类算法基于贝叶斯定理，其数学表达如下：

给定一个文本文档 D 和类别 c，我们想要计算给定文档 D 后，它属于类别 c 的概率 P(c|D)。根据贝叶斯定理，这个概率可以表示为：

$$P(c|D)=\frac{P(D|c)\cdot P(c)}{P(D)}$$

其中：

• $P(c|D)$ 是后验概率，表示在给定文档 D 的情况下，它属于类别 c 的概率。
• $P(D|c)$ 是似然概率，表示在类别 c 的情况下，生成文档 D 的概率。
• $P(c)$ 是先验概率，表示类别 c 在整个数据集中的概率。
• $P(D)$ 是归一化因子，确保后验概率的总和等于 1。

在朴素贝叶斯算法中，对于文档 D，我们通常将其表示为一个特征向量 $X=(x_1,x_2,...,x_n)$，其中 $x_i$ 是文档中出现的第 i 个特征（通常是词语或词汇表中的词），n 是特征的总数。基于朴素贝叶斯的独立性假设，我们可以将似然概率表示为各个特征的条件概率的乘积：

$$P(D|c)=P(x_1|c)\cdot P(x_2|c)\cdot ...\cdot P(x_n|c)$$

这就是朴素贝叶斯的“朴素”之处，因为它假设在给定类别的情况下，各个特征之间是相互独立的。

在实际应用中，我们通常比较各个类别的后验概率，选择具有最大后验概率的类别作为最终的分类结果：

$$\hat{c}=\arg \underset{c}{\max }P(c|D)$$

这就是朴素贝叶斯分类器的基本数学表达式。在文本分类中，特征通常是词语，而条件概率可以通过统计训练数据中属于某一类别的文档中各个词语出现的频率来估计。

2.1.3 一般步骤

在文本分类中，朴素贝叶斯可以用于判定一段文本属于哪个类别，比如垃圾邮件过滤、情感分析等。下面是使用朴素贝叶斯进行文本分类的一般步骤：

• 收集数据： 收集包含已分类文本的数据集，每个文本都被标记为其所属的类别。

• 数据预处理： 对文本数据进行预处理，包括去除停用词（常见但不具有实际意义的词语，如“the”、“and”等）、转换为小写字母，去除标点符号等操作。

• 建立词向量模型： 将文本数据转换为数学表示，通常采用词袋模型（Bag of Words）或词袋模型的改进形式，如TF-IDF（Term Frequency-Inverse Document Frequency）。

• 计算先验概率和条件概率： 对每个类别计算先验概率，即该类别在整个数据集中出现的概率。然后，对于每个词语，计算在给定类别下的条件概率。

• 预测： 对于一个新的文本，根据计算的先验概率和条件概率，使用贝叶斯公式计算每个类别的后验概率，然后选择具有最大后验概率的类别作为文本的分类结果。

2.1.4 简单python代码实现

以下是一个示例，展示如何在Python中使用朴素贝叶斯进行基于特定话题的文本分类。我们将使用一个电影评论数据集，并尝试对评论进行情感分类。

import numpy as np
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.model_selection import train_test_split
from sklearn import metrics

# 构建电影评论
all_comments = [
    "这部电影太棒了，演员演技一流，剧情紧凑扣人心弦。",
    "一部让人感动的电影，推荐给所有的影迷。",
    "情节极其拖沓，演员表演平平，完全不值得一看。",
    "电影画面很美，音乐也很好听，但故事情节有些乏味。",
    "这是一部让人捧腹大笑的喜剧片，非常好看。",
    "失望透顶，剧情乱七八糟，真是浪费时间。",
    "影片虽然有一些硬伤，但整体来说还算可以。",
    "这部电影简直是烂到家了，看了让人生气。",
    "感觉导演对故事没有把握好，留下太多疑问。",
    "非常感动，看完后让人回味无穷。",
    "一部扣人心弦的惊悚片，推荐给喜欢刺激的观众。",
    "这是一部典型的爆米花电影，娱乐性很强。",
    "剧情不错，结尾略显俗套，但总体来说还可以。",
    "对影片的制作水平很满意，期待导演的下一部作品。",
    "一部令人难以忘怀的文艺片，值得一看。",
    "这个故事太老套了，完全没有新意。",
    "影片的氛围营造得非常成功，令人沉浸其中。",
    "这部电影的画面效果太棒了，堪比大片。",
    "看完让人深思，剧情引人入胜。",
    "有点拖沓，看得人有点烦。",
    "这是一部令人惊叹的巨制，影片细腻入微，深刻人心。",
    "剧情跌宕起伏，扣人心弦，是一部不可错过的佳作。",
    "导演功力非凡，演员表现出色，影片质量上乘。",
    "故事情节新颖，让人看得热血沸腾。",
    "影片充满悬念，时不时还能给观众一些惊喜。",
    "虽然是小成本制作，但是影片表现出色，值得一看。",
    "这是一部充满智慧的影片，对人生有很深刻的剖析。",
    "剧情稍显无聊，导演功力有限，不够吸引人。",
    "影片节奏太快，有些情节处理得有点仓促。",
    "缺乏深度，故事单薄，是一部平庸的影片。",
    "这是一部典型的烂片，从头到尾都让人失望透顶。",
]

# 标签：1表示正面，0表示负面
all_labels = [1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 0,
              1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0]

# 将数据集划分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(all_comments, all_labels, test_size=0.15, random_state=12)

# 使用TF-IDF向量化文本数据
vectorizer_nb = TfidfVectorizer()
X_train_nb = vectorizer_nb.fit_transform(X_train)
X_test_nb = vectorizer_nb.transform(X_test)

# 使用朴素贝叶斯模型进行文本分类
model_nb = MultinomialNB()
model_nb.fit(X_train_nb, y_train)
y_pred_nb = model_nb.predict(X_test_nb)

# 输出朴素贝叶斯模型性能报告
print("朴素贝叶斯模型性能报告:\n", metrics.classification_report(y_test, y_pred_nb, zero_division=1))

# 新的文本数据
new_text = ["这是一部非常感人的电影，我热烈推荐。", "电影太差劲，缺乏深度，无聊的很"]

# 将新的文本数据转换为TF-IDF特征向量
X_new = vectorizer_nb.transform(new_text)

# 使用建立好的朴素贝叶斯模型进行预测
predictions = model_nb.predict(X_new)

# 输出预测结果
for text, label in zip(new_text, predictions):
    sentiment = "正面" if label == 1 else "负面"
    print(f"文本: {text}，情感预测: {sentiment}")

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75

运行上述代码后，我们可以得出下面的结果：

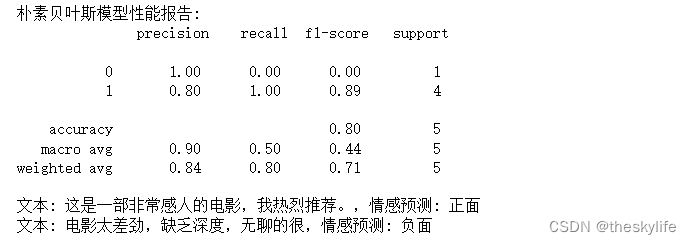
从上述的例子中，我们可以看到模型的性能，以及对文本的预测结果，这样就完成对文本的情感分类，在实际场景中，我们可能会基于更多的文本来进行分类。

---

2.2 支持向量机SVM

支持向量机（Support Vector Machine，SVM）是一种用于二分类和多分类问题的监督学习算法。其主要思想是通过找到能够有效区分不同类别的超平面来进行分类。在文本分类中，SVM可用于将文本数据划分为不同的类别。

2.2.1 基本概念

基本原理：

• SVM通过在特征空间中找到一个能够将不同类别分开的最优超平面来进行分类。
• 最优超平面是指离两个类别的最近样本点（支持向量）最远的决策边界。
• SVM支持线性和非线性分类，具体取决于选择的核函数。

在文本分类中的应用：

• 特征表示： 在文本分类任务中，文本数据需要转换为数值特征。常用的方法包括词袋模型（Bag of Words）和TF-IDF（Term Frequency-Inverse Document Frequency）等。

• Kernel Trick： 当数据不是线性可分时，可以使用核函数将数据映射到高维空间，使其在高维空间中线性可分。在文本分类中，常使用文本特征的内积作为核函数。

• 多分类问题： SVM 本身是一个二分类器，但可以通过一对一（One-vs-One）或一对多（One-vs-All）等策略扩展到多分类问题。

• 参数调整： SVM的性能受到参数选择的影响，包括正则化参数C、核函数的选择等。在文本分类中，通过交叉验证等方法来调整这些参数以优化模型性能。

• 文本向量化： 在进行文本分类前，需要将文本数据向量化。这一步骤可以使用TF-IDF向量化器等工具。

2.2.2 数学公式

线性可分情况：

1）. 超平面方程：
假设有一个d维的特征空间（特征数为d），超平面可以表示为：

$w\cdot x+b=0$

其中：

• $w$ 是法向量（超平面的法向量），表示超平面的方向。
• $x$ 是输入样本的特征向量。
• $b$ 是截距。

对于二分类问题，样本的类别标签为$-1$或$1$。样本点到超平面的函数间隔为：

$f(x)=w\cdot x+b$

分类决策函数为：

$h(x)=\text{sign}(f(x))$

其中：

• $\text{sign}(\cdot )$ 是符号函数，如果参数大于等于0，结果为1，否则为-1。

2).间隔和支持向量：
样本点到超平面的函数间隔为：

$|f(x)|=\frac{1}{\Vert w\Vert }|w\cdot x+b|$

其中：

• $\Vert w\Vert$ 是 $w$ 的范数。

样本点到超平面的几何间隔为：

$\text{distance}(x,\text{Hyperplane})=\frac{1}{\Vert w\Vert }|w\cdot x+b|$

支持向量是离超平面最近的那些训练样本点，它们满足：

$y_i(w\cdot x_i+b)-1=0$

其中：

• $y_i$ 是样本 $x_i$ 的类别标签。

软间隔和松弛变量：

在实际问题中，数据可能不是线性可分的。为了允许一些样本出现在间隔内，引入了松弛变量（slack variable）。

假设有一组松弛变量 ${\xi }_i$，则优化问题变为：

$\min \frac{1}{2}\Vert w{\Vert }^2+C{\sum }_{i=1}^N{\xi }_i$

同时满足约束条件：

$y_i(w\cdot x_i+b)\ge 1-{\xi }_i$

其中：

• $C$ 是一个正则化参数，用于平衡间隔的大小和错误的容忍度。
• ${\xi }_i$ 是第 $i$ 个样本的松弛变量。

核函数和非线性分类：

当数据不是线性可分时，可以通过使用核函数将数据映射到高维空间中，使其在高维空间中变得线性可分。常用的核函数有线性核、多项式核、径向基函数（RBF）核等。

线性核：

$K(x,y)=x\cdot y$

多项式核：

$K(x,y)=(x\cdot y+1{)}^d$

径向基函数（RBF）核：

$K(x,y)=\exp \left(-\frac{\Vert x-y{\Vert }^2}{2{\sigma }^2}\right)$

其中：

• $d$ 是多项式核的次数。
• $\sigma$ 是 RBF 核的带宽参数。

在sklearn中常用的核函数：
在Scikit-learn中，SVC类的kernel参数用于指定支持向量机的核函数。以下是kernel参数支持的主要核函数：

1).线性核函数 (linear)：

• 参数值：kernel='linear'
• 公式：$K(x,y)=x\cdot y$
• 用于线性可分和线性不可分的情况。

from sklearn.svm import SVC

# 使用线性核函数
linear_svm = SVC(kernel='linear')
1
2
3
4

2). 多项式核函数 (poly)：

• 参数值：kernel='poly'
• 公式：$K(x,y)=(x\cdot y+c_0{)}^{degree}$
• degree 参数控制多项式的次数，c_0 是一个常数。

from sklearn.svm import SVC

# 使用多项式核函数，设置次数为3
poly_svm = SVC(kernel='poly', degree=3)
1
2
3
4

3). 径向基函数（RBF）核函数 (rbf)：

• 参数值：kernel='rbf'
• 公式：$K(x,y)=\exp \left(-\frac{\Vert x-y{\Vert }^2}{2{\sigma }^2}\right)$
• gamma 参数控制 RBF 核的带宽。

from sklearn.svm import SVC

# 使用径向基函数核函数，设置带宽参数为0.1
rbf_svm = SVC(kernel='rbf', gamma=0.1)
1
2
3
4

4).Sigmoid 核函数 (sigmoid)：

• 参数值：kernel='sigmoid'
• 公式：$K(x,y)=\tanh (\alpha x\cdot y+c_0)$
• coef0 参数控制函数中的常数项。

from sklearn.svm import SVC

# 使用Sigmoid核函数，设置常数项为0.5
sigmoid_svm = SVC(kernel='sigmoid', coef0=0.5)
1
2
3
4

2.2.3 一般步骤

使用支持向量机（SVM）模型进行文本分类的一般步骤如下：

1).数据准备：

• 收集文本数据集，确保每个样本都有对应的标签（类别）。
• 对文本进行预处理，包括分词、去除停用词、词干提取等，以便得到可用于模型训练的特征。

2).特征提取：

• 将文本数据转换为模型可以理解的特征表示。常用的方法包括词袋模型、TF-IDF 等。
• 对于深度学习方法，可以使用词嵌入（Word Embeddings）等方法得到词向量表示。

3).划分数据集：

• 将数据集划分为训练集和测试集，用于模型的训练和评估。

4).选择模型和核函数：

• 根据问题的性质选择合适的支持向量机模型，如分类任务使用 SVC。
• 选择合适的核函数，可以尝试线性核、多项式核、径向基函数（RBF）核等，根据数据特点调整超参数。

5).训练模型：

• 将训练集输入到支持向量机模型中进行训练。
• 在训练过程中，模型会学习出一个能够区分不同类别的超平面或决策边界。

6).模型评估：

• 使用测试集对训练好的模型进行评估，常用的评估指标包括准确率、精确度、召回率、F1 分数等。
• 根据评估结果调整模型的超参数，提高模型性能。

7).预测新数据：

• 使用训练好的支持向量机模型对新的文本数据进行分类预测。

8).模型解释（可选）：

• 对于黑盒模型，可以尝试使用解释性工具（如 SHAP、LIME）来解释模型的决策过程。

9).优化和调整：

• 根据模型在验证集上的性能进行调整，可能需要尝试不同的特征提取方法、调整核函数参数等。

10).部署模型（可选）：
- 如果模型在测试中表现良好，可以将其部署到生产环境中，用于实际应用。

这些步骤是一个通用的框架，具体的应用时，请根据具体问题和数据的特点而进行适当裁剪。

2.2.4 利用svm进行文本分类

下面我们将会以一些新闻的内容数据进行文本分类，将文本内容归到不同的类别中：

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.svm import SVC
from sklearn.pipeline import Pipeline
from sklearn.metrics import classification_report, accuracy_score
import jieba

# 构建数据集
data = {
    'text': [
        "一家新的科技公司发布了一款革命性的产品。",
        "一场激烈的体育比赛在城市体育馆举行。",
        "科学家发现了一种新的治疗癌症的方法。",
        "政府宣布提高科研经费，支持创新项目。",
        "最新的手机技术将在下个月发布。",
        "环保组织发起全球范围的植树运动。",
        "某公司发布最新款折叠屏手机。",
        "新的医疗技术有望提高手术成功率。",
        "世界各地的科技巨头争相投资量子技术。",
        "一家环保公司发起全球清洁能源倡议。",
        "新型电动汽车在全球市场上取得成功。",
        "科技园区引进国际一流的研发团队。",
        "环保志愿者走进社区，倡导垃圾分类。",
        "全球篮球联赛冠军产生，精彩赛事吸引关注。",
    ],
    'label': ['科技', '体育', '科技', '科技', '科技', '环保', '科技', '科技', '科技', '环保',
              '娱乐', '科技', '环保', '体育']
}

df = pd.DataFrame(data)

# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(df['text'], df['label'], test_size=0.2, random_state=11)

# 中文分词
def chinese_tokenizer(text):
    return list(jieba.cut(text))

# 构建模型
text_clf = Pipeline([
    ('tfidf', TfidfVectorizer(tokenizer=chinese_tokenizer, token_pattern=None)),
    ('svm', SVC(kernel='linear', decision_function_shape='ovr'))
])
# # 其他写法
# tfidf = TfidfVectorizer(tokenizer=chinese_tokenizer, token_pattern=None)
# svm = SVC(kernel='linear', decision_function_shape='ovr')
# text_clf = Pipeline([('tfidf', tfidf), ('svm', svm)])

# 训练模型
text_clf.fit(X_train, y_train)

# 在测试集上进行预测
y_pred = text_clf.predict(X_test)

# 评估模型性能
print("准确率:", accuracy_score(y_test, y_pred))
print("分类报告:\n", classification_report(y_test, y_pred))


# 添加新的新闻内容
new_texts = [
    "一项突破性的环保技术在国际会议上首次亮相。",
    "一家科技公司宣布成功研发出新一代人工智能芯片。",
    "一场精彩的足球比赛在城市体育场上演，吸引了数万名观众。"
]

# 使用模型进行标签预测
predicted_labels = text_clf.predict(new_texts)

# 打印预测结果
for text, label in zip(new_texts, predicted_labels):
    print(f"新闻内容: {text}")
    print(f"预测标签: {label}\n")


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76

运行上述代码后，结果如下：

通过上面的结果，我们可以得到模型的性能非常高，这可能是运气使然，实际运用时基本不会有这么高的准确率。从文本中，我们也看到预测的类别。

---

值得注意的是，这里的代码只是一个简单的示例，实际上在应用中你可能需要进一步调整模型的参数，进行交叉验证等来提高模型的性能。

此外，深度学习模型如卷积神经网络（CNN）和循环神经网络（RNN）在文本分类中也有出色的表现。在使用这些模型时，你可以考虑使用深度学习框架如TensorFlow或PyTorch，以便更好地处理复杂的语义信息。

3. 模型评估和性能优化

一个好的文本分类模型不仅需要选择合适的算法，还需要进行充分的评估和性能优化。

3.1 朴素贝叶斯（Naive Bayes）

模型评估：

• 1).准确率（Accuracy）： 表示分类正确的样本数占总样本数的比例。计算公式为 (TP + TN) / (TP + TN + FP + FN)，其中 TP 为真正例，TN 为真负例，FP 为假正例，FN 为假负例。

• 2).精确度（Precision）： 表示预测为正例中实际为正例的比例。计算公式为 TP / (TP + FP)。

• 3).召回率（Recall）： 表示实际为正例中被正确预测为正例的比例。计算公式为 TP / (TP + FN)。

• 4).F1 分数： 是精确度和召回率的调和平均值，计算公式为 2 * (Precision * Recall) / (Precision + Recall)。

性能优化：

• 1).特征选择： 选择关键特征可以提高模型的性能，可以使用信息增益、卡方检验等方法进行特征选择。

• 2).平滑处理： 在朴素贝叶斯中，当某个词在训练集中未出现时，会导致概率为零，可以使用平滑处理（如拉普拉斯平滑）来避免这个问题。

• 3).处理不平衡数据： 如果正负样本不平衡，可以考虑采用过采样或欠采样等方法来平衡数据。

3.2 支持向量机（SVM）

模型评估

• 1).准确率、精确度、召回率、F1 分数： 同样适用于SVM，采用混淆矩阵来计算这些指标。

• 2).SVM的决策函数： SVM在预测时可以得到样本到超平面的距离，可以根据距离的阈值来调整分类的灵敏度。

性能优化

• 1).核函数选择： SVM的性能高度依赖于核函数的选择，可以尝试不同的核函数（如线性核、多项式核、高斯核等）来找到最适合数据的模型。

• 2).正则化参数（C参数）调优： 调整正则化参数C，以平衡模型的复杂度和训练集拟合度。

• 3).特征工程： 对文本进行适当的特征工程，如使用TF-IDF向量表示文本。

• 4).调整类别权重： 对于不平衡的数据集，可以通过调整类别权重来平衡模型对不同类别的关注度。

• 5).交叉验证： 使用交叉验证来评估模型在不同子集上的性能，确保模型的泛化能力。

此外，随着深度学习技术的不断发展，调整深度学习模型的参数和结构也是提高文本分类性能的有效途径。深度学习模型在学习大规模语料库中的复杂特征方面具有独特优势，可以进一步提升文本分类的水平。

写在最后

通过本文的学习，你不仅了解了文本分类的原理和应用，还掌握了在Python中实现高级文本分类的方法。在解决实际问题时，你可以灵活选择不同的模型和参数，提高分类效果。文本分类作为NLP领域的重要技术，为我们更好地理解和利用文本信息提供了强有力的工具。希望本文能够帮助你在数据分析和数据挖掘的旅程中更进一步。继续保持学习，探索NLP的更多可能性吧！