基于FPGA的数字信号处理（10）--定点数的舍入模式（1）四舍五入round_fpga四舍五入

1、前言

将浮点数定量化为定点数时，有一个避不开的问题：某些小数是无法用有限个数的2进制数来表示的。比如：

0.5(D) = 0.1(B)

0.1(D) = 0.0001100110011001~~~~(B)

可以看到0.5是可以精准表示的，但是0.1却不行。原因是整数是离散的，而小数是连续的。在固定范围内整数的个数是有限个，而小数的个数则是无限个，所以某些小数注定是不能被有限个数的编码来精准表示的。

显然，在工程中不可能做无限位的定点化，我们只能根据需求，确定好精度从而决定定点数的格式。确定好定点数的格式后，有一个无法避免的问题，那就是如何对超过范围的部分进行处理，即如何舍入（Rounding）？

常见的舍入方式有向上取整(ceil)，向下取整（floor），向0取整（fix），四舍五入（round）等等，本文只讨论四舍五入这种舍入方式。

---

2、10进制中的四舍五入

10进制的四舍五入大家都很熟悉了，比如：

1.456保留0位小数，第1位小数是4，小于5，所以向第0位小数（个位）进位0并舍去其他小数位，结果是1

1.456保留1位小数，第2位小数是5，等于5，所以向第1位小数进位1并舍去其他小数位，结果是1.5

1.456保留2位小数，第3位小数是6，大于5，所以向第2位小数进位1并舍去其他小数位，结果是1.46

假如有1个4位小数（整数2位）要舍入到2位小数（整数2位），例如 21.4567 >> 21.46 ，这类转换可以写如下的Verilog伪代码：

wire [5:0]	data_in;	//4位小数,整数2位
wire [3:0]	data_out;	//2位小数,整数2位
wire	carry;			//进位

assign carry = (data_in[1]>4)? 1 : 0;		//判断第3位小数是否大于4，大于4产生进位1，否则产生进位0
assign data_out = data_in[5:2] + carry;		//舍去其他小数位，并加上进位值
1
2
3
4
5
6

---

3、二进制中的四舍五入

2进制的四舍五入和10进制的原理是一样的。10进制的四舍五入，其中的4和5分别代表的是数据的上半部分0_{4和下半部分5}9。2进制没有4和5，只有0和1，所以严格来讲，2进制的四舍五入应该叫 “0舍1入”。

首先对定点数的格式做如下约定：

• Qm.n 表示整体长度为m，小数部分长度为n的有符号定点数。例如，Q8.5表示 1bits符号位 + 2bits整数 + 5bits小数的有符号定点数
• UQm.n表示整体长度为m，小数部分长度为n的无符号定点数。例如，UQ8.5表示 3bits整数 + 5bits小数的无符号定点数

对于10进制的整数和负数的四舍五入，规则如下：

• -1.3四舍五入到，-1.5会四舍五入到-2，-1.8会四舍五入到-2
• 1.3四舍五入到1，1.5会四舍五入到2，1.8会四舍五入到2

比较需要注意的是0.5这类中间数据的处理规则：0.5四舍五入到1，-0.5四舍五入到-1。

这说明四舍五入和符号位是无关的，它只和数据的绝对值有关。但在2进制中，负数不单单只是用符号位来和正数区分的，所以对于二者的处理还是有一些区别。接下来分别讨论。

3.1、无符号数的四舍五入

假设有一个UQ8.6格式的定点数要转换为UQ5.3格式的定点数，要求舍入模式为四舍五入（round）。即用四舍五入的方法保留3位小数，那么只需要判断第4位小数是否为1即可。若为1，则向第3位小数产生进位1，若为0，则向第3位小数产生进位0，其余小数部分舍去。例如

10进制数1.703125的UQ8.6格式为：01_101_101，第4位小数为1，则向第3位小数产生进位1，所以有01_101+1=01_110，这就是该数做了四舍五入后的UQ5.3格式结果，即10进制数1.75。

10进制数3.796875的UQ8.6格式为：11_110_011，第4位小数为0，则向第3位小数产生进位0，所以有11_110+0=11_110，这就是该数做了四舍五入后的UQ5.3格式结果，即10进制数3.75。

接下来就可以写Verilog代码了：

module test(
	input		[7:0]	data_U8Q6,	//无符号数，整数2位，小数6位
	output		[4:0]	data_U5Q3	//无符号数，整数2位，小数3位	
);

reg	carry;	//对高位小数的进位

assign	data_U5Q3 = data_U8Q6[7:3] + carry;
			
always@(*)begin
	//xx.xxx x xx
	//xx.xxx
	//只要判断第4位小数的值是否为1即可
	if(data_U8Q6[2])	//5入	
		carry = 1'b1;
	else				//4舍
		carry = 1'b0;
end
  
endmodule
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

因为当次位的值是1时，就加1；当次位的值是0时，就加0。所以上面的写法和下面的写法是等价的：

assign data_U5Q3 = data_U8Q6[7:3] + data_U8Q6[2];

接下来写个TB测试一下，把转换的结果保存在文本文件**<vivado.txt>**里，后面再跟matlab的转换结果做比较。TB如下：

`timescale 1ns/1ns
module test_tb();

reg		[7:0]	data_U8Q6;
wire	[5:0]	data_U5Q3;

//例化被测试模块
test	test_inst(
	.data_U8Q6		(data_U8Q6),
	.data_U5Q3		(data_U5Q3)
);

integer i;		//循环变量
integer	fid;	//文件句柄

initial begin
	data_U8Q6 = 0;			//赋初值
	fid = $fopen("G:/new/vivado.txt","w");	//打开文件
	
	for(i=0;i<=255;i=i+1)begin	//遍历所有的输入
		data_U8Q6 = i;		
		#5 $fdisplay(fid,"%h",data_U5Q3);	//把对应输出写入文件
	end
	#20 
	$fclose(fid);	//关闭文件
	$stop();		//结束仿真
end

endmodule
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

matlab对定点数的处理就方便很多了，主要需要用到两个函数 fi 和 hex。

• fi 可以生成一个/多个指定格式的定点数
• hex可以将定点数以16进制显示，方便写入文件

matlab代码如下（看注释吧）：

%--------------------------------------------------
% 关闭无关内容
clear;		
close all;
clc;

%--------------------------------------------------
% 确定U8Q6格式的定点数的范围及精度
data_min = 0;				% 确定定点数的最小值	
data_max = 4-1/2^6;			% 确定定点数的最大值	
data_step = 1/2^6;			% 确定定点数的精度即步长	

% 生成U8Q6格式的定点数
% fi(数值，符号位（0正1负），位长，小数长度)
data_fi_U8Q6 = fi(data_min:data_step:data_max,0,8,6);	

% 在U8Q6的基础上生成U5Q3格式的定点数
data_fi_U5Q3 = fi(data_fi_U8Q6,0,5,3);

%--------------------------------------------------
% 把生成的U8Q6数据保存在txt文件
fid = fopen('matlab.txt','w');		% 打开文件

% 往文件写入数据
for k = 1:length(data_fi_U5Q3)
    fprintf(fid, '%s\n', hex( data_fi_U5Q3(k) ) );	% hex可以将fi数据转化为16进制显示
end
fclose(fid);						% 关闭文件
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

这时就分别生成了两个文件：<vivado.txt> 和 <matlab.txt> ，只要比对两个文件的内容，就可以知道RTL代码有没有问题了。比对两个文件的方法可太多了，比如用matlab对比，或者直接在TB里对比也行，看你自己喜好吧。

因为这里数据量不多，所以我是直接打开两个文件用插件对比的，仿真结果有一点小小的问题，下面四个数据是对不上的：

左边是matlab的对照输出，右边是RTL的输出。这四个数据分别是二进制的：

• 11_111_100
• 11_111_101
• 11_111_110
• 11_111_111

matlab四舍五入后的结果是 0x1F 即5bits的11_111，而RTL的结果则是 0x00 即5bits的00_000，这是数据明显溢出了，因为我们没有设计对应的溢出保护机制，所以结果就出错了。关于溢出的几种处理方式在前两篇文章已经讲过了，这里就不讲了。

3.2、有符号数的四舍五入

讨论有符号数的四舍五入处理之前，需要先了解两个问题：

1. 如何根据有符号数的补码快速求得对应的数值？
2. 将定点数的小数部分截断，在数值上相当于什么操作？

（1）如何根据有符号数的补码快速求得对应的数值？

我相信很多人在把一个负数的补码转换成求其10进制数值时采取的方法是将其转化按位取反（除符号位外）+1，然后再把数值位都加起来。例如：

求4’b1010对应的十进制数，首先按位取反，得到4‘b1101，再加1，得到4’b1110，最高位是负数的符号位，剩余的3位是数值，即4+2=6，所以最终的结果是-6.

其实有更加简便的方法的，那就是让符号位也参与运算，但是权重是负的，例如：

求4’b1010对应的十进制数，即 -8 + 0 + 2 + 0 = -6

（2）将定点数的小数部分截断，在数值上相当于什么操作？

例如通过直接截断方式把Q4.2格式的定点数转换成Q2.0格式的，实际上就是直接去除小数部分。去除小数部分，实际上就相当于在数值上向下取整（floor）。例如：

1.75向下取整是 1，对应的定点数01_11截掉小数部分就是01（1），二者的结果是一致的。

-1.75向下取整是 -2，对应的定点数10_01截掉小数部分就是10（-2），二者的结果也是一致的。

现在可以继续讨论如何实现有符号数的四舍五入了。

其实直接套用上面的方法也可以对有符号数做四舍五入，只是有一个例外，那就是对小数部分是0.5的这类数需要特殊处理。为了方便说明，接下来以Q4.2格式转Q2.0格式为例（实际上就是对小数做四舍五入）。

10_10（-1.5）和11_10（-0.5）这两个数按理来讲的四舍五入结果应该是：

-1.5 >> -2，即10_10 >> 10

-0.5 >> -1，即11_10 >> 11

如果用老办法，那就是 整数位直接加第1位小数的值 ，所以结果应该是：

10_10 >> 10 + 1 >> 11 即-1

11_10 >> 11 + 1 >> 00 即0

虽然二者的处理结果是不同的，但也只是一个舍入到了左边的整数，一个舍入到了右边的整数，二者在精度上是一致的。如果算法不对这方面做特别的要求或者要求比较松，这种方法其实也是可以用的。这种方法最大的好处就是省资源，因为它不用判断0.5这类特殊情况嘛。

如果你希望严格遵守四舍五入的定义，那么我们接着分析。

从上面我们知道了，负数的最高位是可以参与加法的，所以计算一个负数的数值时，可以分为以下3种情况：

（1）要截掉的小数位的最高位为1，且剩余位全为0。

例如Q4.2转Q2.0，即xx.10，小数的最高位的值是0.5，剩余小数部分都是0则部分的和是0，相加说明小数的值为0.5，加上整数部分的值后，整个定点数应该是个x.5 类型的小数。

因为-1.5是舍入到-2（相当于向下取整）。所以这种情况的处理方式为：

先把小数部分去除（相当于向下取整），然后在+0（这样可以把电路复用起来）。

例如1.5舍入到2，即01.10除去小数位即01，然后再加1即 01 + 1 =10（2）；-1.5舍入到 -2，即10.10除去小数位即10，然后再加0即 10 + 0 =10（-2）。

（2）要截掉的小数位的最高位为1，且剩余位不全0

最高位为1表示的值是0.5，其他位不全为0，说明小数部分的值是(0.5,1)，上面说过了，最高位的符号位是可以参加到数值的运算的，所以正数部分的值是个负数，整数 + 小数后 ，其小数部分的值的绝对值就处于（0,0.5）范围内了。比如：

-1.25即10.11，小数部分11的值是0.5+0.25 = 0.75，在(0.5,1)范围内，整数部分的值一定是负的即 -2 + 0 = -2 ，二者相加后 -2 + 0.75 = -1.25，其小数部分的值的绝对值就在（0,0.5）范围内了。

因为这个范围内的值舍入都是向上取整的，例如 -1.25>> -1，-1.375>> -1。所以这种情况的处理方式为：

先把小数部分去除（相当于向下取整），然后在+1（二者相当于实现了向上取整操作）

（3）要截掉的小数位的最高位为0

小数的最高位为0，说明整个小数的部分不会超过0.5，加上整数部分的负数后，整个定点数的值的小数部分的绝对值肯定在范围(0.5,1)。例如：

-1.75即10.01，小数部分01的值是0+0.25 = 0.25，在(0，0.5)范围内，整数部分的值一定是负的即 -2 + 0 = -2 ，二者相加后 -2 + 0.25 = -1.75，其小数部分的值的绝对值就在（0.5,1）范围内了。

因为这个范围内的值舍入都是向下取整的，例如 -1.75 >> -2，-1.875 >> -2。所以这种情况的处理方式为：

先把小数部分去除（相当于向下取整），然后在+0（实际上只要去除小数部分就可以了，再加0是为了把电路复用起来）

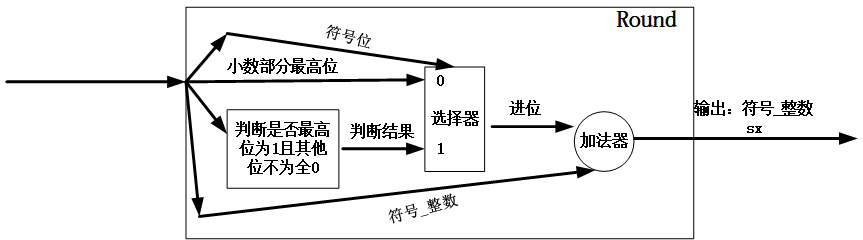
可以采用与无符号数的转换类似的例子：

将一个Q8.6格式的定点数要转换为Q5.3格式的定点数，要求舍入模式为四舍五入（round）。

根据上面的分析，可以写如下的Verilog伪代码，首先出掉多余的小数位，并加上进位：

assign	data_5Q3 = data_8Q6[7:3] + carry;
1

然后对不同的情况来判断应该加的进位值：

if(~data_8Q6[7])begin	//是正数
	if(data_8Q6[2])		//5入	
		carry = 1'b1;	//即carry = data_8Q6[2]
	else				//4舍
		carry = 1'b0;	//即carry = data_8Q6[2]
end
else begin				//是负数
	if(data_8Q6[2] && (|data_8Q6[1:0]))		//如果最高位为1，且剩余位不全为0
		carry = 1'b1;	//即carry = data_8Q6[2] && (|data_8Q6[1:0])
	else
		carry = 1'b0;	//即carry = data_8Q6[2] && (|data_8Q6[1:0])
end
1
2
3
4
5
6
7
8
9
10
11
12
13

上面的判断可以简化一下：

assign	carry = data_8Q6[7] ? (data_8Q6[2] && (|data_8Q6[1:0]) ) : data_8Q6[2]	
1

综上，这部分的Verilog代码如下：

module test(
	input	[7:0]	data_8Q6,	//有符号数，符号位1位，整数2位，小数6位
	output	[4:0]	data_5Q3	//有符号数，符号位1位，整数2位，小数3位	
);

wire	carry;	//对高位小数的进位

assign	carry = data_8Q6[7] ? (data_8Q6[2] && (|data_8Q6[1:0]) ) : data_8Q6[2];
assign	data_5Q3 = data_8Q6[7:3] + carry;
  
endmodule
1
2
3
4
5
6
7
8
9
10
11

这一次，我们先用matlab生成所有的Q8.6格式的定点数和Q5.3格式的定点数，然后把Q8.6格式的定点数通过TB输入到RTL模块，观察RTL输出的Q5.3格式的定点数和matlab生成的是否一致，就可判断电路是否设计正确。

matlab部分代码如下：

%--------------------------------------------------
% 关闭无关内容
clear;
close all;
clc;

%--------------------------------------------------
% 确定8Q6格式的定点数的范围及精度
data_min = -2^1;		% 确定定点数的最小值	
data_max = 2-1/2^6;     % 确定定点数的最大值	
data_step = 1/2^6;      % 确定定点数的精度即步长	

F = fimath('RoundingMethod','round');					% 设定定点数的溢出模式为四舍五入
% fi(数值，符号位（0正1负），位长，小数长度)
data_fi_8Q6 = fi(data_min:data_step:data_max,1,8,6,F);	% 生成8Q6格式的定点数

% 在8Q6的基础上生成5Q3格式的定点数
data_fi_5Q3 = fi(data_fi_8Q6,1,5,3,F);					

%--------------------------------------------------
% 把生成的8Q6数据保存在txt文件
fid_8Q6 = fopen('matlab_8Q6.txt','w');
for k = 1:length(data_fi_8Q6)
    fprintf(fid_8Q6, '%s\n', hex( data_fi_8Q6(k) ) );
end
fclose(fid_8Q6);

%--------------------------------------------------
% 把生成的5Q3数据保存在txt文件
fid_5Q3 = fopen('matlab_5Q3.txt','w');
for k = 1:length(data_fi_5Q3)
    fprintf(fid_5Q3, '%s\n', hex( data_fi_5Q3(k) ) );
end
fclose(fid_5Q3);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

然后编写TB，导入输入和输出，并将两个输出做比对，如果二者不一致则错误统计+1，最后观察错误个数即可。

`timescale 1ns/1ns
module tb_test();

reg		[7:0]	data_8Q6;
wire	[4:0]	data_5Q3;

//例化被测试模块
test	test_inst(
	.data_8Q6		(data_8Q6),
	.data_5Q3		(data_5Q3)
);

integer i;								//循环变量

reg	[7:0]	data_8Q6_ref	[0:255];	//将matlab生成的8Q6输入保存到该memory中，做为标准输入
reg	[4:0]	data_5Q3_ref	[0:255];	//将matlab生成的5Q3输出保存到该memory中，作为比对的参考
reg	[8:0]	err;						//错误统计计数器

//从文件中读取数据写入到MEM中
initial begin
	$readmemh("G:/matlab_test/matlab_8Q6.txt",data_8Q6_ref);	
	$readmemh("G:/matlab_test/matlab_5Q3.txt",data_5Q3_ref);	
end

initial begin
	data_8Q6 = 0;	//赋初值
	err = 0;
	
	for(i=0;i<=255;i=i+1)begin	//遍历所有的输入，共256个
		data_8Q6 = data_8Q6_ref[i];				//载入matlab生成的输入		
		#5; 
		if(data_5Q3 != data_5Q3_ref[i])begin	//如果matlab的输出和RTL的输出不同
			err = err + 1;						//错误个数加1
			$display("fixed input:%b	matlab output:%b	RTL output:%b",data_8Q6_ref[i],data_5Q3_ref[i],data_5Q3);
		end	
		else
			err = err;
	end
	#20 
	if(err == 'd0)
        $display("pass");
	else
        $display("fail,there is %d errors",err);
	$stop();		//结束仿真
end

endmodule
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

仿真结果如下，有四个地方是对不上的：

和上面的无符号数的情况是一样，因为电路没有设计溢出保护，所以数据溢出了，因为matlab是有溢出处理的，所以二者的结果会对不上。