盐析白兔

这个屌丝很懒，什么也没留下！

热门标签

2022年4月第十三届蓝桥杯C/C++程序设计A组（省赛）试题及题解_蓝桥杯a组真题

作者：盐析白兔 | 2024-03-24 14:17:02

踩

蓝桥杯a组真题

试题A：裁纸刀

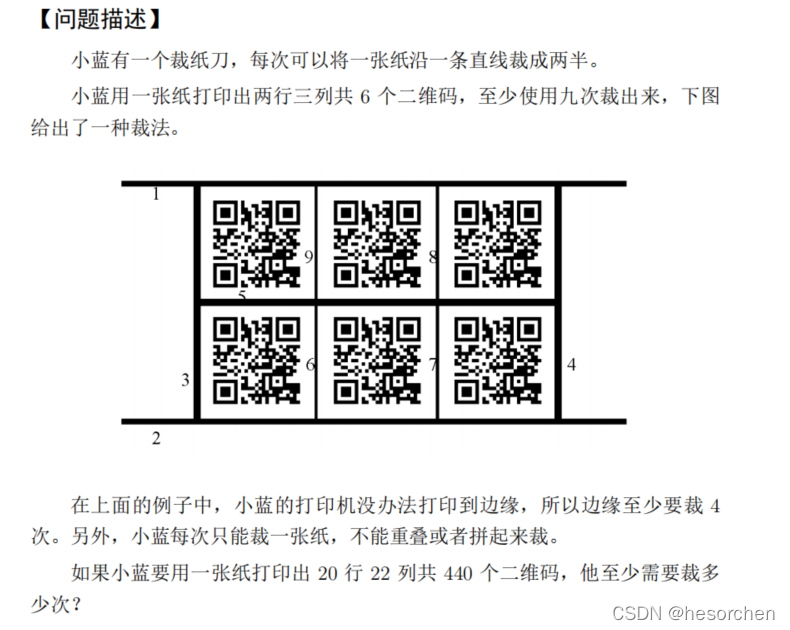
在这里插入图片描述

答案为 $n * m - 1 + 4$

443

试题B：灭鼠先锋

在这里插入图片描述

LLLV

试题C：求和

在这里插入图片描述

预计得分100%

思路：维护一个前缀 $s u m$ 即可。

总时间复杂度 $O (n)$

参考代码：

#include <bits/stdc++.h>
using namespace std;

const int N = 2e5 + 5;

int a[N];

void solve()
{
    int n;
    scanf("%d", &n);
    long long ans = 0, sum = 0;
    for (int i = 1; i <= n; i++)
    {
        scanf("%d", &a[i]);
        ans += sum * a[i];
        sum += a[i];
    }
    cout << ans << endl;
}
int main()
{
    solve();
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

试题 D: 选数异或

**在这里插入图片描述**

预计得分100%

对于每个位置 $i$ ，设 $y = a [i]$ ^ $x$ ，找到最近的一个 $y$ 的下标 $i d x$ ，记作 $b [i]$ 。再用线段树维护 $b$ 数组的区间最大值 $ma xx$ ，如果 $ma xx >= L$ ，那么为 $yes$ 。

总时间复杂度 $O (n l o g n)$

参考代码：

#include <bits/stdc++.h>
using namespace std;

const int N = 3e5 + 5;

int a[N], b[N];

struct node
{
    int l, r, val, maxx;
} tr[N * 4];

void pushup(int k) { tr[k].maxx = max(tr[k * 2].maxx, tr[k * 2 + 1].maxx); }
void build(int k, int l, int r)
{
    tr[k].l = l;
    tr[k].r = r;
    if (tr[k].l == tr[k].r)
    {
        tr[k].val = tr[k].maxx = b[l];
        return;
    }
    int mid = l + r >> 1;
    build(k * 2, l, mid);
    build(k * 2 + 1, mid + 1, r);
    pushup(k);
}

int query(int k, int l, int r)
{
    if (tr[k].l == l && tr[k].r == r)
        return tr[k].maxx;
    int mid = tr[k].l + tr[k].r >> 1;
    if (r <= mid)
        return query(k * 2, l, r);
    else if (l > mid)
        return query(k * 2 + 1, l, r);
    else
        return max(query(k * 2, l, mid), query(k * 2 + 1, mid + 1, r));
}

void solve()
{
    int n, m, x;
    scanf("%d %d %d", &n, &m, &x);
    for (int i = 1; i <= n; i++)
        scanf("%d", &a[i]);
    map<int, int> last;
    for (int i = 1; i <= n; i++)
    {
        int y = a[i] ^ x;
        if (!last.count(y))
            b[i] = -1;
        else
            b[i] = last[y];
        last[a[i]] = i;
    }
    build(1, 1, n);
    while (m--)
    {
        int l, r;
        scanf("%d %d", &l, &r);
        int maxx_pos = query(1, l, r);
        puts(maxx_pos >= l ? "yes" : "no");
    }
}

int main()
{
    solve();
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72

试题 E: 爬树的甲壳虫

在这里插入图片描述

暂时不会。

试题 F: 青蛙过河

在这里插入图片描述

2022.4.25 UPDATE：少了一个语句，已修正

预计得分100%

二分经典题改编题，一眼二分，check有点难写。

check思路：

可以令 $d p [i]$ 表示跳到第 $i$ 个石头的最大次数。
把最后 $mi d$ 个石头的 $d p [i]$ 加起来， $s u m >= 2 * x$ 即合法。

总时间复杂度 $O (n l o g n)$

参考代码：

#include <bits/stdc++.h>
using namespace std;

const int N = 3e5 + 5;
int a[N];

long long dp[N];
// dp[i]表示最多能跳到位置i dp[i]次

int n, x;
bool check(int mid)
{
    long long sum = 0;
    for (int i = 1; i <= mid; i++) //前mid个都可以
        dp[i] = a[i];
    int l = 1;
    for (int i = mid + 1; i <= n; i++)
    {
        while (i - l > mid)//控制跳跃距离。
            ++l;
        dp[i] = 0;
        while (dp[i] < a[i] && l < i)
        {
            if (dp[l] + dp[i] <= a[i])
            {
                dp[i] += dp[l];
                dp[l] = 0;
                ++l;
            }
            else
            {
                dp[l] -= a[i] - dp[i];
                dp[i] = a[i];
            }
        }
    }
    long long ans = 0;
    int L = n - mid + 1;
    for (int i = L; i <= n; i++)
        ans += dp[i];
    return ans >= 2 * x;
}

void solve()
{
    scanf("%d %d", &n, &x);
    --n;
    for (int i = 1; i <= n; i++)
        scanf("%d", &a[i]);
    int l = 1, r = n, ans = n + 1;
    while (l <= r)
    {
        int mid = l + r >> 1;
        if (check(mid))
        {
            ans = mid;
            r = mid - 1;
        }
        else
            l = mid + 1;
    }
    printf("%d\n", ans);
}

int main()
{
    solve();
    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70

试题 G: 最长不下降子序列

在这里插入图片描述

预计得分10% ~ 30%

暴力思路：

枚举修改位置，二分法 $O (n l o g n)$ 求最长不下降子序列，（跳过中间那段长度为 $k$ 的数组）

总时间复杂度 $O(n^2logn)$

参考代码：

#include <bits/stdc++.h>
using namespace std;

const int N = 1e5 + 5;

int a[N], dp[N];
int n, k;
int LIS(int L, int R) //二分求LIS
{
    int len = 0;
    dp[len] = -0x3f3f3f3f;
    for (int i = 1; i <= n; i++)
    {
        if (i == L) //跳过k个
        {
            i = R;
            continue;
        }

        if (a[i] >= dp[len])
        {
            ++len;
            dp[len] = a[i];
        }
        int p = upper_bound(dp + 1, dp + 1 + len, a[i]) - dp;
        dp[p] = a[i];
    }
    return len;
}
void solve()
{
    scanf("%d %d", &n, &k);
    for (int i = 1; i <= n; i++)
        scanf("%d", &a[i]);
    if (n - 1 <= k)
    //修改k个必然能全部满足
    {
        printf("%d\n", n);
        return;
    }
    int ans = k + 1;
    for (int i = 1; i + k - 1 <= n; i++)
        ans = max(ans, k + LIS(i, i + k - 1));
    printf("%d\n", ans);
}

int main()
{
    solve();
    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

试题 H: 扫描游戏

在这里插入图片描述

预计得分10% ~ 30%

暴力思路：

极角排序。之后每次暴力扫描，循环直到扫描不到物品。

总时间复杂度 $O(n^2)$

参考代码：

#include <bits/stdc++.h>
using namespace std;

const int N = 3e5 + 5;
const int INF = 0x3f3f3f3f;
struct node
{
    long long x, y, z, id;
    double theta;
    bool operator<(const node &tmp) const { return theta < tmp.theta; }
};

vector<node> vec;
int out[N];
node tmp;
void solve()
{
    int n;
    long long L;
    scanf("%d %lld", &n, &L);
    for (int i = 1; i <= n; i++)
    {
        out[i] = -1;
        tmp.id = i;
        scanf("%lld %lld %lld", &tmp.x, &tmp.y, &tmp.z);
        tmp.theta = atan2(tmp.y, tmp.x);
        vec.push_back(tmp);
    }
    sort(vec.begin(), vec.end());
    int len = (int)vec.size();
    int p = -1;
    for (int i = len - 1; i >= 0; i--)
    {
        if (vec[i].x >= 0)
        {
            p = i;
            break;
        }
    }
    if (p == -1)
    {
        for (int i = len - 1; i >= 0; i--)
        {
            if (vec[i].y <= 0)
            {
                p = i;
                break;
            }
        }
    }

    if (p == -1)
        p = (int)vec.size() - 1;

    vector<node> tmp = vec;
    vec.clear();
    for (int i = p; i >= 0; i--)
        vec.push_back(tmp[i]);
    for (int i = (int)tmp.size() - 1; i > p; i--)
        vec.push_back(tmp[i]);
    int rk = 0, sum = 0;
    node pre;
    pre.theta = INF;
    while (1)
    {
        vector<node> now;
        int m = vec.size();
        for (int i = 0; i < m; i++)
            if (vec[i].x != INF)
                now.push_back(vec[i]);
        m = now.size();
        bool flag = 0;
        for (int i = 0; i < m; i++)
        {
            if (L * L >= now[i].x * now[i].x + now[i].y * now[i].y)
            {
                L += now[i].z;
                now[i].x = INF; //标记
                flag = 1;
                if (fabs(now[i].theta - pre.theta) <= 1e-6)
                    out[now[i].id] = rk;
                else
                {
                    rk = sum + 1;
                    out[now[i].id] = rk;
                }
                sum++;
                pre = now[i];
            }
        }
        if (!flag)
            break;
        vec = now;
    }
    for (int i = 1; i <= n; i++)
        printf("%d%c", out[i], i == n ? '\n' : ' ');
}
int main()
{
    solve();
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102

试题 I: 数的拆分

在这里插入图片描述

预计得分10%

暴力思路：筛出所有质因子，不能有出现次数只有一次的质因子，并且最多有两个出现次数为奇数次的质因子（出现偶数次只需均分给 $x_1$ 和 $y_1$ ）

总时间复杂度 $O (t s q r t (n))$

参考代码：

#include <bits/stdc++.h>
using namespace std;

bool check(long long x)
{
    map<int, int> mp;
    for (int i = 2; i * i <= x; i++)
    {
        if (x % i == 0)
            while (x % i == 0)
            {
                x /= i;
                mp[i]++;
            }
    }
    if (x >= 2)
        mp[x]++;
    int odd = 0, flag = 0;
    for (auto it : mp)
    {
        if (it.second == 1)
            return 0;
        if (it.second & 1)
            odd++;
        if (it.second >= 2)
            flag = 1;
    }
    return odd <= 2;
}
void solve()
{
    int t;
    scanf("%d", &t);
    while (t--)
    {
        long long x;
        scanf("%lld", &x);
        puts(check(x) ? "yes" : "no");
    }
}

int main()
{
    solve();
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

试题 J: 推导部分和

在这里插入图片描述

暂时不会。

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/盐析白兔/article/detail/302882

2022年4月第十三届蓝桥杯C/C++程序设计A组（省赛）试题及题解_蓝桥杯a组真题

目录

试题A：裁纸刀

试题B：灭鼠先锋

试题C：求和

试题 D: 选数异或

试题 E: 爬树的甲壳虫

试题 F: 青蛙过河

试题 G: 最长不下降子序列

试题 H: 扫描游戏

试题 I: 数的拆分

试题 J: 推导部分和