- 1tsconfig.js配置属性含义-编译上下文_allowjs": true是开启什么
- 2软件系统质量属性_2.面向架构评估的质量属性
- 3基于opencv和python的人脸识别签到系统设计与实现_python课堂签到系统
- 4MySQL8.0安装教程
- 5【opencv】示例-detect_mser.cpp 使用 MSER 算法来检测图像中的极值区域
- 6猫头虎分享:什么是Promise异步编程
- 7学深度学习的实现路径_小学数学深度学习认识及实践路径
- 8建议收藏:超详细ChatGPT(GPT 4.0)论文润色指南+最全提示词咒语_chat gpt 润色论文
- 9基于预训练模型 ERNIE-Gram 实现语义匹配-数据预处理_预训练语言模型 语义匹配
- 10书写高质量代码之状态维护_生命周期函数不进行实际业务代码书写
单指标时间序列异常检测——基于重构概率的变分自编码(VAE)代码实现(详细解释)_vae重构概率
赞
踩
1. 编写目的
不少论文都是基于VAE完成的异常检测,比如 Donut 、Bagel。尽管 Donut 实现的模型很容易通过继承于重写父类方法的方式实现一个 VAE-baseline,并且 Bagel 中自带了一个 VAE-baselina(感兴趣的小伙伴可以前去查看一下源码),但为了简化过程,详细解释 VAE 用于单指标时间序列异常检测的方法,我重新实现了一个简单的 VAE-baselina,并进行了详细的解释,希望可以帮助到需要的小伙伴们。
可以的话,点个赞并发表评论吧 ~ 一定回复 ~~
2. 参考资料
| 名称 | 链接 |
|---|---|
| vae + 重构概率 => 异常检测 | https://blog.csdn.net/smileyan9/article/details/109255466 |
| donut 进行了一定的改进的 vae | https://blog.csdn.net/smileyan9/article/details/112307506 |
| Bagel 条件变分自编码 | https://smileyan.blog.csdn.net/article/details/113463339 |
| tensorflow官网实现->卷积 vae | https://tensorflow.google.cn/tutorials/generative/cvae |
| 龙书作者 vae 源码 | https://github.com/dragen1860/TensorFlow-2.x-Tutorials/blob/master/12-VAE/main.py |
版权声明
未经本人 (smile-yan) 允许,不得转发与转载。
3. 源代码
整个项目的源码地址为:https://github.com/smile-yan/vae-anomaly-detection-for-timeseries,觉得可以的话,顺手点个星星吧,感谢~
3.1 网络结构
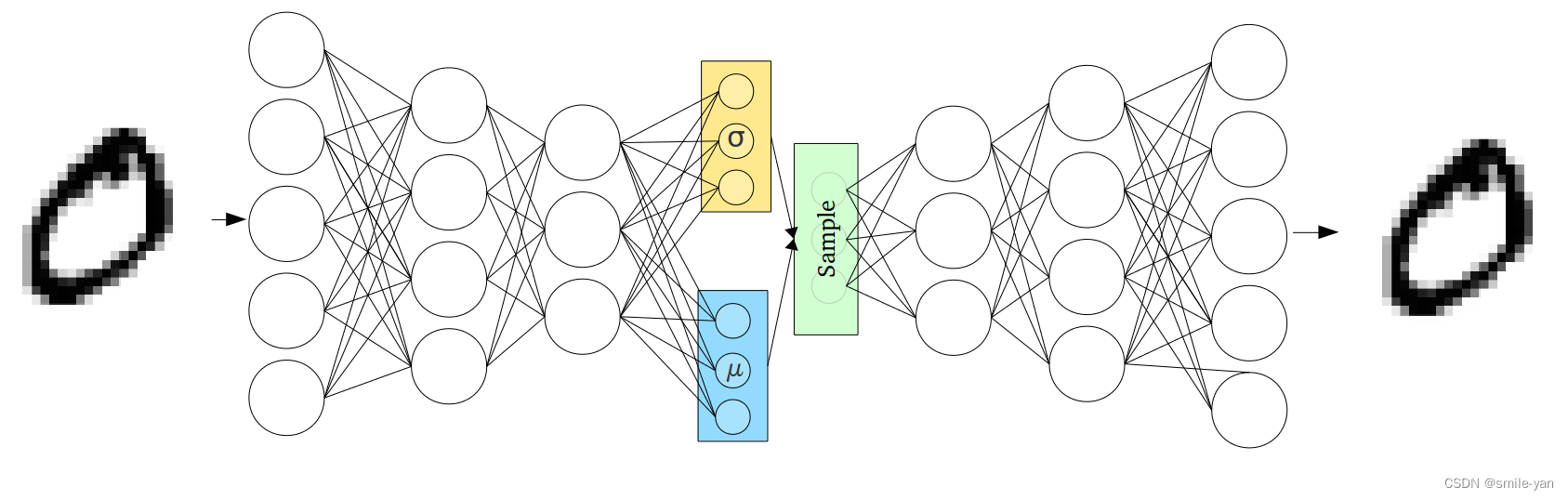
图片源地址为龙书作者开源地址 https://github.com/dragen1860/TensorFlow-2.x-Tutorials/tree/master/12-VAE
我们简化整个过程,写到 VAE 的初始化函数中如下所示:
class VAE(tf.keras.Model):
def __init__(self, latent_size=4):
super(VAE, self).__init__()
# 与输入数据对接
self.fc1 = tf.keras.layers.Dense(100)
# fc1 => μ and log σ^2
self.fc2 = tf.keras.layers.Dense(latent_size)
self.fc3 = tf.keras.layers.Dense(latent_size)
# decode
self.fc4 = tf.keras.layers.Dense(100)
# 试图还原原始数据
self.fc5 = tf.keras.layers.Dense(120)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
所以这个部分可以概述为 fc1 与 fc2 构成了 encode 的过程,此过程完成以后,我们可以得到由 μ \mu μ 和 log σ 2 \log \sigma^2 logσ2 组成的隐变量。
而 decode 过程则是分两步还原原始数据。
3.2 encode 过程
初始化过程只是初始化我们要用的变量,真正的 编码过程从这个函数开始,这个过程是非常简单的,可以看作盲盒降维操作。
def encode(self, x):
"""encode过程,返回 μ 和 log σ^2
:param x: 单窗口数据
:return: μ 和 log σ^2
"""
h = tf.nn.relu(self.fc1(x))
# mu, log_variance
return self.fc2(h), self.fc3(h)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
3.3 decode 过程
为了重用方便,将 decode 按照是否使用 sigmoid 函数分为两个过程,这个与 https://tensorflow.google.cn/tutorials/generative/cvae 的 decode 函数添加一个参数的效果是一样的。
def decode_logits(self, z):
h = tf.nn.relu(self.fc4(z))
return self.fc5(h)
def decode(self, z):
return tf.nn.sigmoid(self.decode_logits(z))
- 1
- 2
- 3
- 4
- 5
- 6
3.4 概率密度方法(Probability Density Function)
decode 过程可以分为两个步骤,如下面右图所示,可以理解为
g
(
z
)
g(z)
g(z) 对应的是一个数据分布,而
g
(
z
)
g(z)
g(z) 以后的就是重构数据,也就是说重构数据可以理解为从这个分布中采样而得到的,当然,深度神经网络采样过程是模糊的,所以这样的对应关系可以理解为采样得到的,至于怎么采样就是神经网络的参数调整过程了。
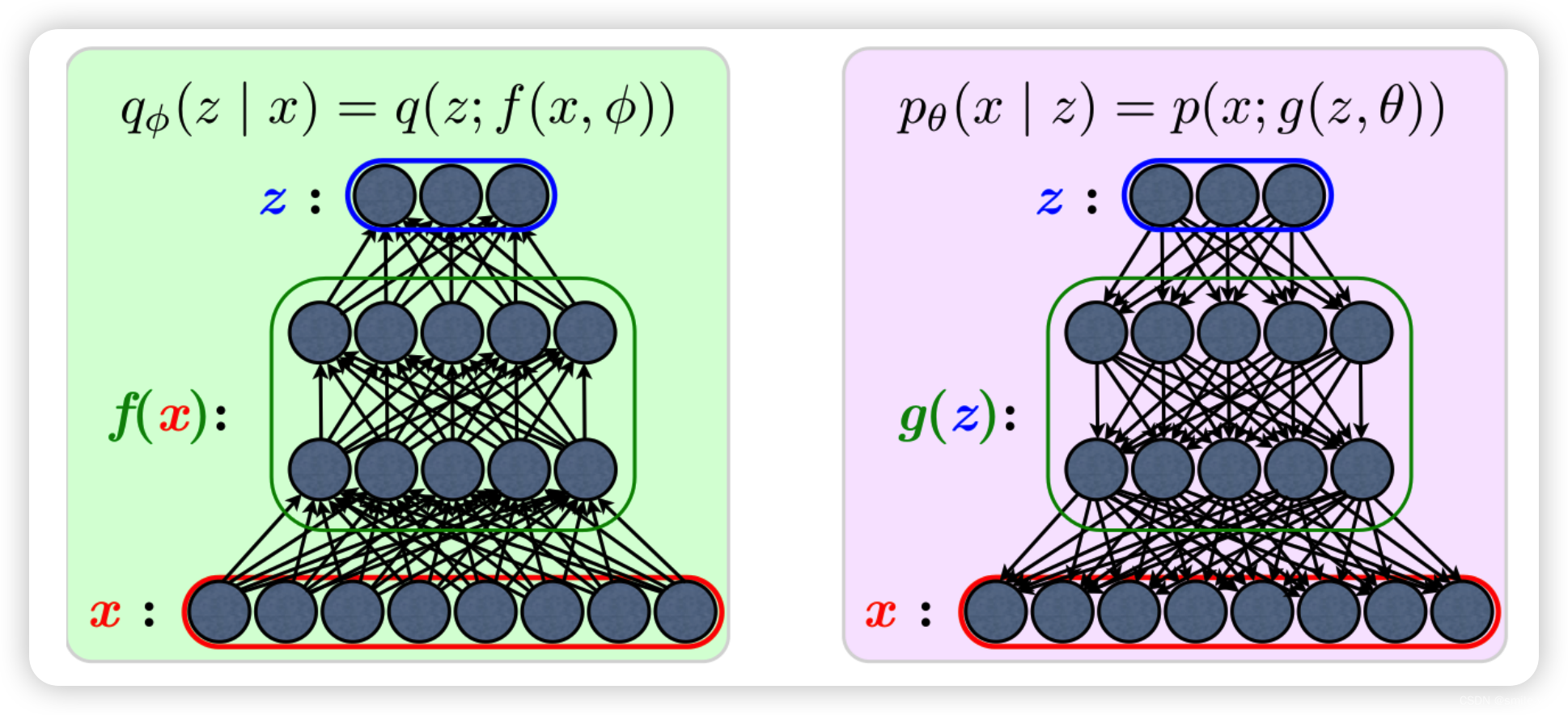
所以训练目标,就是使得得到的分布
g
(
z
)
g(z)
g(z) 中采样得到的
x
′
x'
x′ 尽可能地接近于观测数据
x
x
x。接下来我们计算重构概率就是基于这个理论:
使用正常数据训练模型后,对于测试数据 x t x_t xt:
- 如果它是正常数据,那么它在 g ( z ) g(z) g(z) 对应的分布中,分布密度较大;
- 如果它是异常数据,那么它在 g ( z ) g(z) g(z) 对应的分布中,分布密度较小。
所以计算一个测试数据的重构概率,实质就是计算这个 g ( z ) g\ (z) g (z) 分布中的分布密度。
考虑到没有基础的小伙伴们,现在我们快速需要介绍一下分布密度的计算:
这里是参考维基百科的内容 https://en.wikipedia.org/wiki/Probability_density_function :

更一般的情况,我们会计算分布密度的对数值,这里做一个简单的公式推导:
log_normal_pdf ( x ; μ , σ 2 ) = log 1 σ 2 π e − 1 2 ( x − μ σ ) 2 = − log ( σ 2 π ) − 1 2 ( x − μ σ ) 2 = − log σ − 1 2 log 2 π − 1 2 ( x − μ σ ) 2 = − 1 2 ( log σ 2 + log 2 π + ( x − μ ) 2 σ 2 ) (1) \text{log\_normal\_pdf}\ (x; \mu, \sigma^2) = \log \frac{1}{\sigma\sqrt{2\pi}} \ e^{-\frac{1}{2}(\frac{x-\mu}{\sigma})^2} \\ = - \log\ (\sigma \sqrt{2\pi}) - {\frac{1}{2}(\frac{x-\mu}{\sigma})^2} \\ = - \log \sigma - \frac{1}{2} \log 2\pi - {\frac{1}{2}(\frac{x-\mu}{\sigma})^2} \\ = -\frac{1}{2}\bigl(\log \sigma^2 + \log 2\pi + \frac{(x-\mu)^2}{\sigma^2}\bigr) \tag{1} log_normal_pdf (x;μ,σ2)=logσ2π 1 e−21(σx−μ)2=−log (σ2π )−21(σx−μ)2=−logσ−21log2π−21(σx−μ)2=−21(logσ2+log2π+σ2(x−μ)2)(1)
所以我们可以得到一个 log_normal_pdf 的 python 代码,如下所示:
def log_normal_pdf(sample, mean, log_var, axis=1):
log2pi = tf.math.log(2. * np.pi)
return tf.reduce_sum(-.5 * ((sample - mean) ** 2. * tf.exp(-log_var) + log_var + log2pi), axis=axis)
- 1
- 2
- 3
在后面的内容中我们会多次用到这个计算方法。
3.5 重参数化
重参数化过程就是建立 z z z 与 μ \mu μ 、 σ \sigma σ 之间的关系,为了简化这个关系一般都会直接使用最简单的线性关系(同时也要考虑到梯度下降的需要),所以会令
z = μ + ε ⋅ σ (2) z = \mu + \varepsilon \cdot \sigma \tag{2} z=μ+ε⋅σ(2)
这个对应的python 代码实现非常简单:
def reparameterize(mu, log_var):
"""重参数化,计算隐变量 z = μ + ε ⋅ σ
:param mu: 均值
:param log_var: 方差的 log 值
:return: 隐变量 z
"""
std = tf.exp(log_var * 0.5)
eps = tf.random.normal(std.shape)
return mu + eps * std
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
3.6 VAE 的损失函数 ELBO 的计算
在 《VAE 模型基本原理简单介绍》 中我们已经比较了解了VAE的面貌,VAE 的损失函数 ELBO 的计算方法如下公式:
log p ( x ) ≥ ELBO = E q ( z ∣ x ) [ log p ( x , z ) q ( z ∣ x ) ] (3) \log p(x) \ge \text{ELBO} = \mathbb{E}_{q(z|x)}\left[\log \frac{p(x, z)}{q(z|x)}\right] \tag{3} logp(x)≥ELBO=Eq(z∣x)[logq(z∣x)p(x,z)](3)
为了方便我们利用对数函数的性质拆解成三个式子的和:
ELBO = E q ( z ∣ x ) [ log p ( x ∣ z ) + log p ( z ) − log q ( z ∣ x ) ] (4) \text{ELBO} = \mathbb{E}_{q(z|x)}\left[ \log p(x| z) + \log p(z) - \log q(z|x) \right] \tag{4} ELBO=Eq(z∣x)[logp(x∣z)+logp(z)−logq(z∣x)](4)
像这种条件概率计算一般可以使用蒙特卡洛方法进行求解,也就转换成 从特定分布
q
(
z
∣
x
)
q(z|x)
q(z∣x) 中采样得到
z
z
z ,然后计算一下式子的值:
log
p
(
x
∣
z
)
+
log
p
(
z
)
−
log
q
(
z
∣
x
)
(5)
\log p(x| z) + \log p(z) - \log q(z|x) \tag{5}
logp(x∣z)+logp(z)−logq(z∣x)(5)
现在开始写代码求解这个式子:
def compute_loss(model, x):
mean, log_var = model.encode(x)
z = reparameterize(mean, log_var)
x_logit = model.decode_logits(z)
cross_ent = tf.nn.sigmoid_cross_entropy_with_logits(logits=x_logit, labels=x)
log_p_x_z = -tf.reduce_sum(cross_ent)
log_p_z = log_normal_pdf(z, 0., 0.)
log_q_z_x = log_normal_pdf(z, mean, log_var)
return -tf.reduce_mean(log_p_x_z + log_p_z - log_q_z_x)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
因为最终我们需要的是一个double类型的数值,所以最后一步是 tf.reduce_mean。
3.7 训练过程
@tf.function
def train_step(model, x, optimizer):
with tf.GradientTape() as tape:
loss = compute_loss(model, x)
gradients = tape.gradient(loss, model.trainable_variables)
optimizer.apply_gradients(zip(gradients, model.trainable_variables))
- 1
- 2
- 3
- 4
- 5
- 6
3.8 重构概率计算函数
这个地方一定要参考原论文 《Variational Autoencoder based Anomaly Detection using Reconstruction Probability》,关于重构概率的计算,原文中的描述为:
The reconstruction probability that is calculated here is the Monte Carlo estimate of
E
q
ϕ
(
z
∣
x
)
[
log
p
θ
(
x
∣
z
)
]
E_{q_\phi(z|x)}[\log p_\theta (x|z)]
Eqϕ(z∣x)[logpθ(x∣z)], the second term of the right hand side of equation (7).
摘录其中的算法截图如下:

为了观看更加方便,我们把
x
(
i
)
x^{(i)}
x(i) 看作一次测试数据,这里的对应是一个窗口的数据,所以整个过程,我们写一下:
- μ \mu μ, σ \sigma σ = encoder ( x ) \text{encoder}(x) encoder(x);
- 进行 L L L 次重参数化,得到 L L L 个 z z z,也可以理解为 L L L 个正态分布 z ∼ N ( μ z ( i ) , σ z ( i ) ) z\sim \mathcal{N}\bigl(\mu_{z^{(i)}},\sigma_{z^{(i)}}\bigr) z∼N(μz(i),σz(i));
- 对于每一个
z
∼
N
(
μ
z
(
i
)
,
σ
z
(
i
)
)
z\sim \mathcal{N}\bigl(\mu_{z^{(i)}},\sigma_{z^{(i)}}\bigr)
z∼N(μz(i),σz(i)),进行 decode 操作,并计算 每一次重构数据与原始数据(观测数据)之间的差异。换句话说,decode 之后,在添加 sigmoid 之前,计算
log_p_x_z作为本次数据的重构概率。
def reconstruction_prob(self, x, L=10):
mean, log_var = self.encode(x)
samples_z = []
for i in range(L):
z = reparameterize(mean, log_var)
samples_z.append(z)
reconstruction_prob = 0.
for z in samples_z:
x_logit = self.decode_logits(z)
cross_ent = tf.nn.sigmoid_cross_entropy_with_logits(logits=x_logit, labels=x)
log_p_x_z = -tf.reduce_sum(cross_ent)
reconstruction_prob += log_p_x_z
return reconstruction_prob / L
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
3.9 数据窗口化处理
给定一个时序数据,不断切片,处理成多个窗口数据。
3.10 寻找最合适的重构概率阈值
异常检测是一个二分类任务,因此需要寻找一个合适的重构概率阈值,与每一个点的重构概率进行比较大小,从而确定是否为异常。
关于如何找到最合适的阈值可以参考我以前的一篇博客 快速求解 best F1-score 以及对应的阈值。
4. 直接入手 demo
4.1 clone 到本地
$ git clone git@github.com:smile-yan/vae-anomaly-detection-for-timeseries.git
- 1
4.2 安装依赖
依赖比较少,主要就是 tensorflow 2.x
$ cd vae-anomaly-detection-for-timeseries
$ pip install -r requirement.txt
- 1
- 2
4.3 运行 demo
$ python main.py
- 1
输出效果如下:
The size of train_value_windows is 12179.
The size of test_value_windows is 5151.
Epoch: 1/2, test set ELBO: -38.2476, train time elapse : 77.35 s, test time elapse : 10.38 s
Epoch: 2/2, test set ELBO: -37.8864, train time elapse : 76.15 s, test time elapse : 10.94 s
Epoch: 1/2, test set ELBO: -38.2476, train time elapse : 77.35 s, test time elapse : 10.38 s
Epoch: 2/2, test set ELBO: -37.8864, train time elapse : 76.15 s, test time elapse : 10.94 s
The best threshold: 0.3978
The best f1-score: 0.4375
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
4.4 任何疑问欢迎留言
如果查看源码遇到不理解之处,结合本文依然不能理解的话,请在下面评论,一定想办法解决问题。感谢支持~~
如果觉得不错,请务必点个赞吧~~您的支持是我更新的最大动力。
5. 总结
VAE 用于异常检测的 demo 拖了好久,向各位道歉 ~ 主要是写博客确确实实不能当饭吃,官方也不会打赏啥的,而我只求个点赞,感谢各位的理解与支持。
提前祝各位中秋快乐~
Smileyan
2022.9.6 14:50


