【数据结构】外部排序与最佳归并树_最佳归并树虚段数

外部排序

• （1）按照内存大小，将大文件分成若干长度为 l 的子文件（l 应小于内存的可使用容量），然后将各个子文件依次读入内存，使用适当的内部排序算法对其进行排序，将排好序的归并段重新写入外存，为下一个子文件排序腾出内存空间；

  （2）对得到的归并段进行合并，直至得到整个有序的文件为止。

  下图为2路归并示例

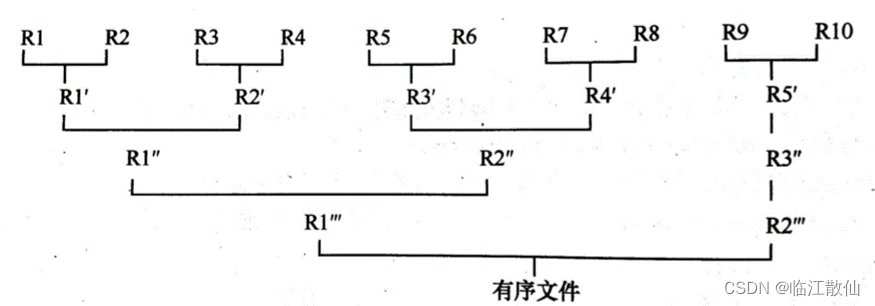
• 基本方法

  例如，有一个含有 10000 个记录的文件，但是内存的可使用容量仅为 1000 个记录，毫无疑问需要使用外部排序算法，具体分为两步：

  • 将整个文件其等分为 10 个临时文件（每个文件中含有 1000 个记录），然后将这 10 个文件依次进入内存，采取适当的内存排序算法对其中的记录进行排序，将得到的有序文件（初始归并段）移至外存。
  • 对得到的 10 个初始归并段进行如图 1 的两两归并，直至得到一个完整的有序文件。

  对于外部排序算法来说，影响整体排序效率的因素主要取决于读写外存的次数，即访问外存的次数越多，算法花费的时间就越多，效率就越低。

  对于同一个文件来说，对其进行外部排序时访问外存的次数同归并的次数成正比，即归并操作的次数越多，访问外存的次数就越多。（每一次归并进行一次读写操作）

  除此之外，一般情况下对于具有 m 个初始归并段进行 k-路平衡归并时，归并的次数为：s=[$lo{g}_{k}m$]（其中 s 表示归并次数，向上取整）。进行内部排序时，可用的内存工作区的大小决定了一次内部排 序可以产生的有序序列的长度l ，m也随其而限定。

  改进：

  （1）增加 k-路平衡归并中的 k 值；

  （2）尽量减少初始归并段的数量 m，即增加每个归并段的容量；

  

  采用 2-路平衡归并时，若每次从 2 个文件中想得到一个最小值时只需比较 1 次；而采用 5-路平衡归并时，若每次从 5 个文件中想得到一个最小值就需要比较 4 次。

  K增大，内部归并时间也增大。 可能抵消由于增大k而减少外存信息读写时间所得的效益。

  改进1：多路归并排序——败者树

  两个结点进行比较，双亲结点记录比较的败者，胜者去参加更高一层的比赛

  

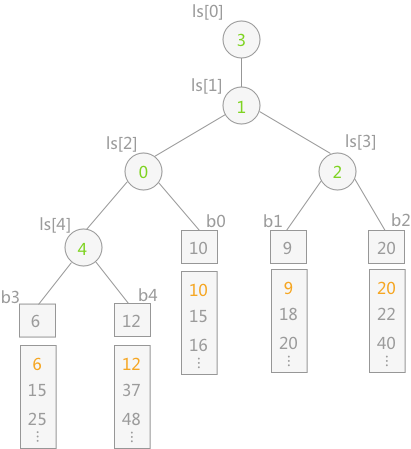
  改进2：减少初始归并段的个数m-置换选择排序

  如果要想减小 m 的值，在外部文件总的记录数 n 值一定的情况下，只能增加每个归并段中所包含的记录数 l。

  1. 首先从初始文件中输入6(内存工作区大小)个记录到内存工作区中；
  2. 从内存工作区中选出关键字最小的记录，将其记为 MINIMAX 记录；
  3. 然后将 MINIMAX 记录输出到归并段文件中；
  4. 此时内存工作区中还剩余 5 个记录，若初始文件不为空，则从初始文件中输入下一个记录到内存工作区中；
  5. 从内存工作区中的所有比 MINIMAX 值大的记录中选出值最小的关键字的记录，作为新的 MINIMAX 记录；
  6. 重复过程 3—5，直至在内存工作区中选不出新的 MINIMAX 记录为止，由此就得到了一个初始归并段；
  7. 重复 2—6，直至内存工作为空，由此就可以得到全部的初始归并段。

  

  

  

  

  置换-选择算法的子序列长度分析：

  输入文件中记录的关键字为随机数时，所得初始归并段的平均 长度为内存工作区大小的2倍。

  在上述创建初始段文件的过程中，需要不断地在内存工作区中选择新的 MINIMAX 记录，即选择不小于旧的 MINIMAX 记录的最小值，此过程需要利用“败者树”来实现。

  在不断选择新的 MINIMAX 记录时，为了防止新加入的关键字值小的的影响，每个叶子结点附加一个序号位，当进行关键字的比较时，先比较序号，序号小的为胜者；序号相同的关键字值小的为胜者。

  

  

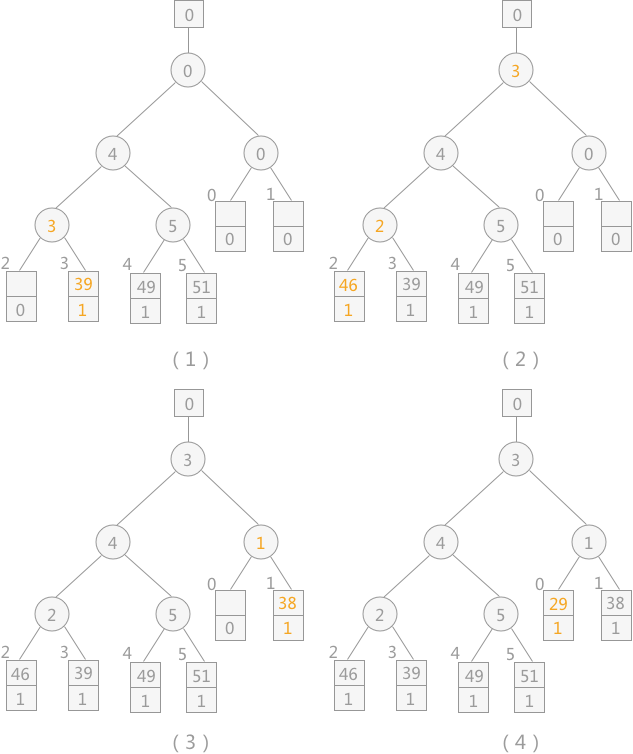
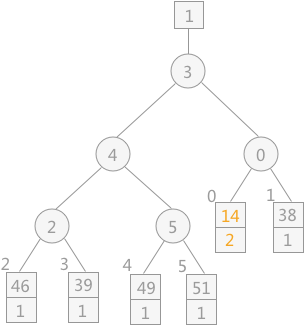
  注意：当读入新的记录时，如果其值比刚刚输出的 MINIMAX 大，其序号则仍为 1；反之则为 2 ，比较时序号 1 比序号 2的记录大。

  通过不断地向败者树中读入记录，会产生多个 MINIMAX，直到最终所有叶子结点中的序号都为 2，此时产生的新的 MINIMAX 值的序号 2，表明此归并段生成完成，而此新的 MINIMAX 值就是下一个归并段中的第一个记录。

• 最佳归并树

  
  
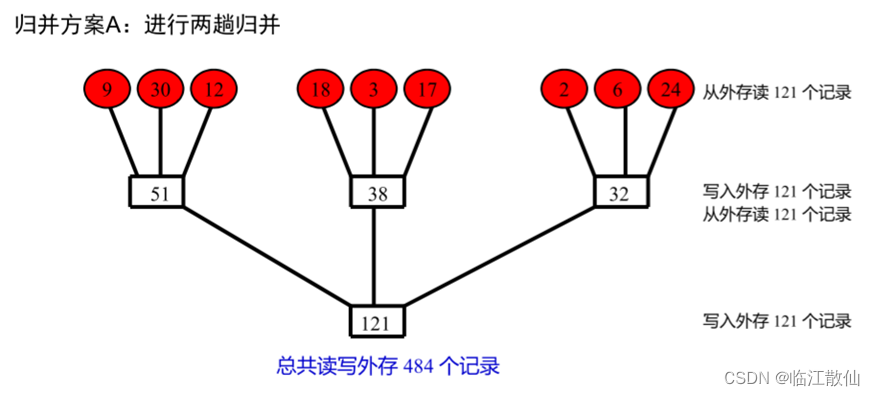
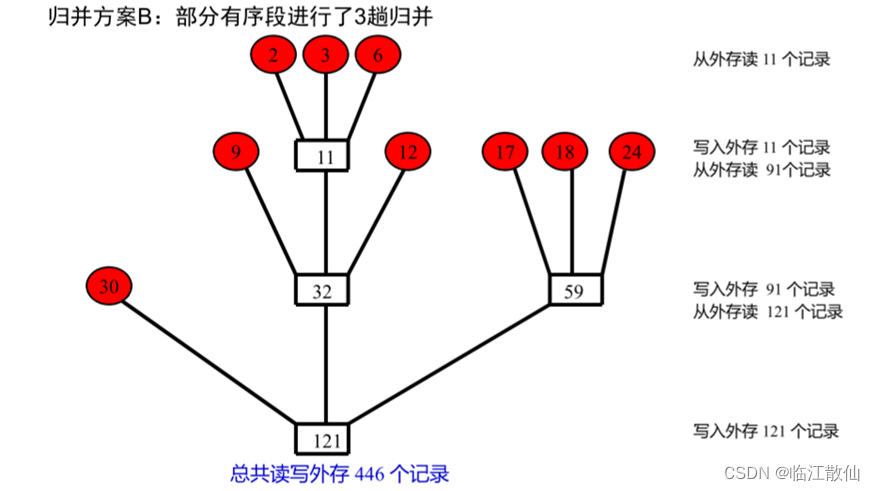
  初始归并段的长度看成是归并树中叶子结点的权，求最佳归并树即求叶子结点带权路径长度最短的树。

  Huffman算法——寻找具有最小加权外部路径长度的二叉树的方法。

  按照 Huffman 树的思想，记录少的段最先合并。

  归并段数量不足时，附加长度为“0”的虚段

  

  

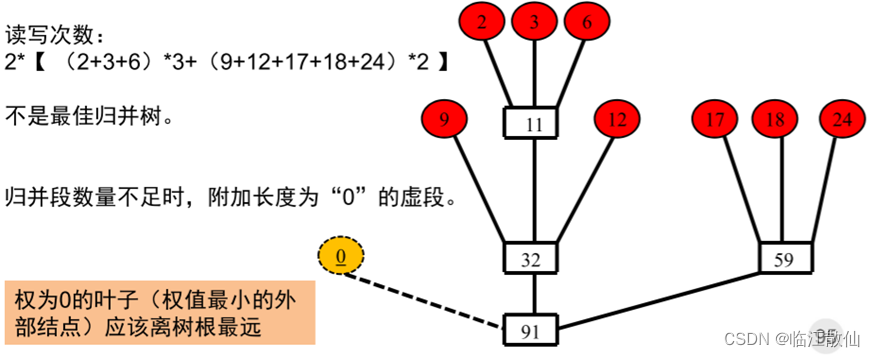
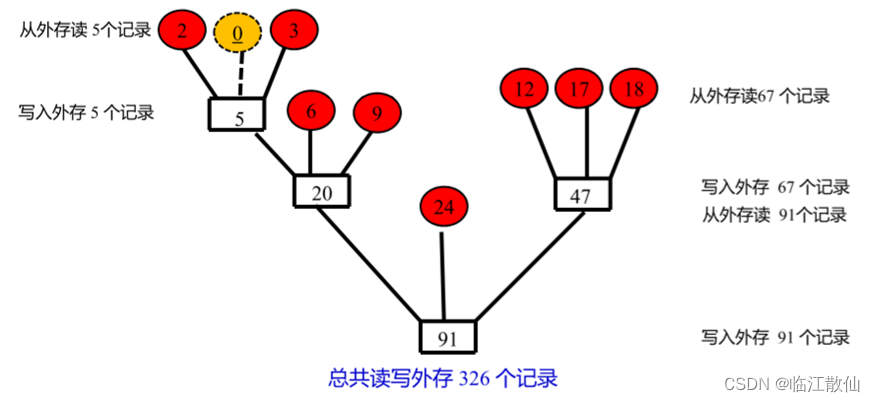
  如何判断附加虚段的数目？

  

  若（m-1）MOD（k-1）=0,则不需要加虚段。 否则，需附加 （k-1）-（m-1）MOD（k-1）个虚段。即第一趟归并参加的实际归并段为（m-1）MOD（k-1）+1

• 小结

  （1）外部排序小结：

  （2）使用“置换-选择”排序产生若干初始归并段。

  （3）确定k。

  （4）根据“最佳归并树”的方法，确定归并方案。
  （5）使用k-路平衡归并完成若干趟归并。