2024五一杯数学建模竞赛A题完整成品论文和代码分析：建立钢板切割的工艺路径动态规划、贪心与分层优化模型_五一杯成品论文

2024五一杯数学建模竞赛A题：建立钢板切割的工艺路径动态规划、贪心与分层优化模型

2024五一数学建模A题完整代码和成品论文获取↓↓↓↓↓

https://www.yuque.com/u42168770/qv6z0d/gyoz9ou5upvkv6nx?singleDoc#

本文文章较长，建议先目录。经过不懈的奋战，目前我们已经完成了2024五一数学建模竞赛A题的40+页完整论文和代码，相关完整内容可见文末参考，

代码为A题全部问题的代码，论文包括摘要、问题重述、问题分析、模型假设、符号说明、模型的建立和求解（问题1模型的建立和求解、问题2模型的建立和求解、问题3模型的建立和求解、问题4模型的建立和求解）、模型的评价等等

文章较长，建议可以先看目录，部分图片如下：

摘要

本文针对钢板切割的工艺路径优化问题，从实际工程背景出发，通过分析影响切割路径的各种因素，提出了一系列具有针对性和创新性的数学模型和优化算法，有效地解决了从简单到复杂的一系列钢板切割优化问题。

针对直线切割路径优化问题，本文将其抽象为图论中的最小权重哈密尔顿回路问题，建立了以切割线段为边、切割起点和交点为节点的图模型。在此基础上，设计了一种基于动态规划的精确算法，通过预处理和状态压缩技术，将算法复杂度降低。本文的创新点在于，充分利用了切割路径的几何特征，提出了一种高效实用的动态规划算法，为后续复杂切割路径优化奠定了基础。

在复杂曲线切割优化问题中，本文提出了一种曲线离散化与逼近的方法，通过等距采样将圆弧、椭圆等曲线转化为折线段，从而将复杂切割简化为直线切割。在此基础上，本文设计了一种基于贪心构造和2-opt局部搜索的切割路径优化启发式算法。该算法首先按照贪心策略生成初始解，然后通过局部邻域搜索对解进行迭代改进。本文的一个创新点是，针对复杂切割提出了高效的离散化与局部搜索相结合的策略，在保证求解质量的同时大幅提升了计算效率。（后面的摘要略，见完整版本）

问题重述

由于篇幅有限，对2024五一杯数学建模竞赛A题的问题重述略。下面直接开始问题分析：

问题分析

2024年五一数学建模A题的分析如下

首先,从整体上看,本题目以钢板切割路径优化为背景,提出了一系列具有实际工程意义和挑战性的子问题。这些子问题涉及到切割路径的几何拓扑、切割顺序约束、嵌套零件切割以及"过桥"连接等多个方面,覆盖了切割加工过程中的关键决策和影响因素。

接下来,我们对各个子问题进行逐一分析:

问题1分析

问题1要求在给定的简单切割布局下设计最优切割路径,使得空程总长度最小。这实际上是一个经典的图论问题,即在切割线段构成的无向图中寻找最短哈密顿路径或回路。尽管问题的概念和形式比较简单,但其计算复杂度却非常高,属于NP-hard问题。为了高效地求解这一问题,我们需要根据切割布局的特点和规模,选择适当的优化建模方法和求解算法,如整数规划、动态规划、启发式搜索等 。

问题2分析

问题2在问题1的基础上,引入了更复杂的切割布局,包括锯齿型外轮廓、圆形和椭圆形内轮廓等曲线切割元素。这些曲线切割元素增加了问题的几何复杂度,使得切割路径的拓扑结构和距离度量变得更加多样化和非线性。为了建模和求解这一问题,我们需要将曲线切割元素离散化和线性化,转化为由直线段组成的近似切割布局,然后在此基础上应用问题1的建模和求解方法。同时,我们还需要针对曲线切割元素的特点,设计合适的离散化方案和逼近策略,在保证逼近精度的同时,兼顾计算效率和优化性能。

问题3分析

问题3在问题2的基础上,进一步引入了内部嵌套零件的切割要求,即要求先切割内部的小矩形零件,再切割外部的椭圆轮廓。这实际上是一个具有优先级约束的组合优化问题,需要在切割路径优化的同时,考虑不同切割对象之间的先后顺序和依赖关系。为了建模和求解这一问题,我们可以采用分层优化的思想,将问题分解为两个子问题:内部零件的切割路径优化和外部轮廓的切割路径优化。这两个子问题可以用不同的优化模型和算法来处理,如TSP模型、最短路模型等,并通过迭代和反馈机制来协调它们之间的耦合和互斥关系。

问题4分析

问题4在问题3的基础上,进一步引入了"过桥"的概念,即在相邻的小矩形零件之间设置一定宽度的连接区域,以防止切割后零件掉落。"过桥"的引入不仅增加了切割路径优化的难度,还带来了新的决策变量和约束条件,即"过桥"的数量、位置和切割时机。为了建模和求解这一问题,我们可以将其转化为一个混合整数非线性规划问题,并采用分支定界、外逼近、罚函数等方法进行求解。同时,我们还可以考虑启发式算法,如遗传算法、模拟退火算法等,通过智能搜索和优化,在合理的时间内找到近似最优解。

模型假设

本文对2024五一数模A题问题1到问题4的模型建立与求解过程中,我们使用了以下几个主要的模型假设:

1. 切割路径的几何抽象假设:我们假设切割路径可以抽象为图论中的哈密顿路径或哈密顿回路,即每个切割点或切割线段对应图中的一个节点,相邻切割点或切割线段之间的切割路径对应图中的一条边,从而将切割路径优化问题转化为在图上寻找最短哈密顿路径或回路的问题。

2. 切割代价的距离度量假设:在计算切割路径的代价或长度时,我们通常假设切割点或切割线段之间的距离可以用某种几何距离度量来衡量,如欧氏距离、曼哈顿距离等,从而将切割路径长度表示为各边距离的加权求和。

3. 切割顺序的线性化假设:（略）

4. "过桥"的几何简化假设:（略）

5. 切割路径的连续化假设:（略，完整见文末参考）

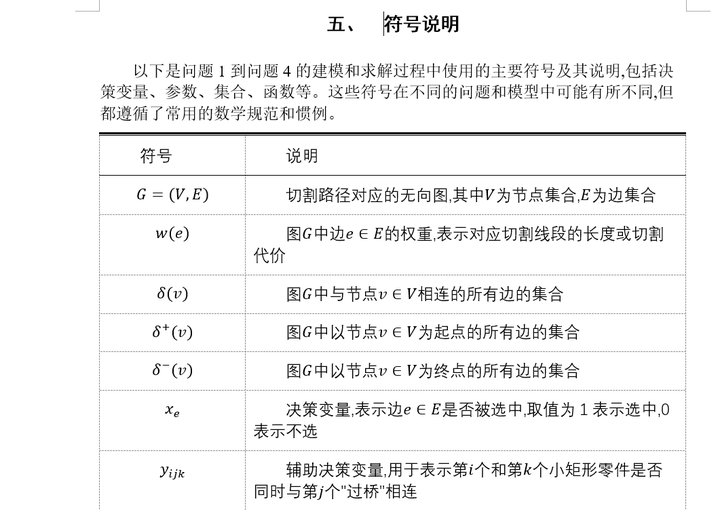
符号说明（部分）

以下是问题1到问题4的建模和求解过程中使用的主要符号及其说明,包括决策变量、参数、集合、函数等。这些符号在不同的问题和模型中可能有所不同,但都遵循了常用的数学规范和惯例。

模型的建立与求解（部分）

问题一模型的建立

首先,让我们来分析一下问题1的特点和求解思路。问题1给出了一个相对简单的下料切割布局N1,要求设计最优切割路径方案,使得空程总长度最小。这里的关键是如何合理地安排切割线的切割顺序,以避免不必要的空程。直观地看,我们希望切割路径尽可能地连续,减少起点到各个切割线之间的来回移动。同时,由于切割起点固定为布局的右下角点,我们还希望优先切割靠近起点的切割线,延迟切割远离起点的切割线。这样可以避免切割路径的"交叉",降低空程长度。

问题一最小权重哈密尔顿回路问题建模

基于以上分析,我们可以将问题1抽象为一个图论问题。具体地,我们将切割线看作图的边,切割线的交点和端点看作图的节点,那么整个切割布局就对应着一个无向图。在该图中,我们需要找到一条经过所有边且总权重最小的哈密尔顿回路,其中边的权重定义为两个节点之间的曼哈顿距离。这样,问题1就转化为了一个经典的图论优化问题——最小权重哈密尔顿回路问题。

接下来,我们来建立问题1的数学模型。设切割布局N1对应的无向图为