opencv系列-图像配准_c++ openc光流法配准

前言：配准方面的知识，在工作中多有用到，对于原理了解一些，但是知之不深，最近时间比较充裕，专门写一篇文章，加深对配准方面知识的学习。

一、简介

通俗定义：给定两幅图像P1,P2，图像配准算法的目标是找到一种变换T: $\Omega 1$ $\Omega 2$，使得变换某一图后，两幅图像的相似程度达到最大。

二、应用场景

Panorama全景拼接；recognition识别；SLAM（同步定位与地图绘制）；去噪；hdr算法

三、算法分类

Feature based; Optical Flow based;CNN based

四、特征点

特征检测。手动或者可能自动检测显著和独特的对象(闭合边界区域，边缘，轮廓，交线，角点等)。为了进一步处理，这些特征可以通过点来表示(重心，线尾，特征点)，这些点称为控制点(CP)。
特征匹配。建立场景图像和参考图像特征之间的相关性。使用各种各样的特征描述符，相似性度量，连同特征的空间相关性。
转换模型估计。估计将感测图像和参考图像对齐的所谓映射函数的类型和参数。映射函数的参数通过特征相关性计算。
图像重采样和转换。使用映射函数转换感测图像。使用合适的插值技术计算非整数坐标的图像值。

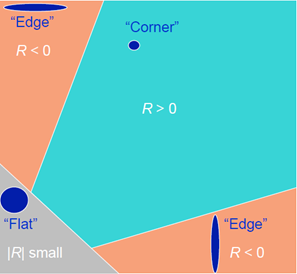
4.1 Haris

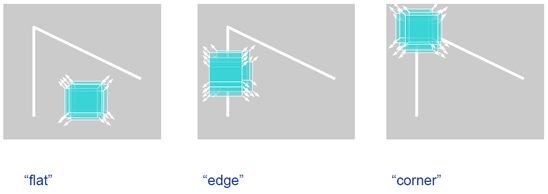
window fuction:

SIFT

SURF

五、特征匹配

Opencv特征寻找及匹配的步骤有哪些？

1. 根据特征点定义寻找特征点
2. 对特征点进行描述
3. 将寻找到的关键点和现有特征点，利用描述符进行量化后，进行匹配。

六、全局配准

坐标旋转变换公式的推导

围绕原点的旋转

$s=r\ast cos(b+a)=r\ast cos(a)\ast cos(b)-r\ast sin(a)\ast sin(b)$
$t=r\ast sin(b+a)=r\ast sin(b)\ast cos(a)+r\ast sin(a)\ast cos(b)$
$x=r\ast cos(a)$
$y=r\ast sin(a)$
将x，y带入s，y当中：
$s=x\ast cos(b)-y\ast sin(b)$
$t=x\ast sin(b)+y\ast cos(b)$
写成矩阵的形式：
[ s t ] = [ c o s ( b ) − s i n ( b ) s i n ( b ) c o s ( b ) ] [ x y ]

$$\begin{bmatrix} s \\ t \end{bmatrix}$$ = $$\begin{bmatrix} cos(b) & -sin(b) \\ sin(b) & cos(b) \end{bmatrix}$$ $$\begin{bmatrix} x \\ y \end{bmatrix}$$ [st​]=[cos(b)sin(b)​−sin(b)cos(b)​][xy​]

坐标系（逆时针）的旋转

以P点坐标为例，在原始坐标系中坐标是（x,y）,在新的坐标系中的坐标为（s,t）
$s=os=oa+as=y\ast sin(\theta )+x\ast cos(\theta )$
$t=ot=ay-by=y\ast cos(\theta )-x\ast sin(\theta )$
写成矩阵的形式：
[ s t ] = [ c o s ( θ ) s i n ( θ ) − s i n ( θ ) c o s ( θ ) ] [ x y ]

$$\begin{bmatrix} s \\ t \end{bmatrix}$$ = $$\begin{bmatrix} cos(\theta) & sin(\theta) \\ -sin(\theta) & cos(\theta) \end{bmatrix}$$ $$\begin{bmatrix} x \\ y \end{bmatrix}$$ [st​]=[cos(θ)−sin(θ)​sin(θ)cos(θ)​][xy​]

绕某一点进行旋转

待补充

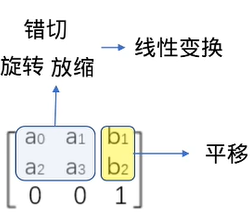
仿射变换

仿射变换（Affine Transformation or Affine Map），在几何上，是一个向量空间，经过线性变换和平移转换为另外一个向量空间的操作。仿射变换的特点，保持图像的平移性（直线仍然是直的）和平行性（平行线仍然平行，且直线点上的位置顺序不变）。
常见的三种变换操作：

• 旋转（rotation）
  坐标系顺时针，内容逆时针
  $$\left[\begin{array}{cc}cos(\theta )& -sin(\theta )\\ sin(\theta )& cos(\theta )\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]=\left[\begin{array}{c}{x}_1\\ y_1\end{array}\right]$$
• 平移（translation）
  $$\left[\begin{array}{ccc}1& 0& T_x\\ 0& 1& T_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}X\\ Y\\ 1\end{array}\right]=\left[\begin{array}{c}X+T_x\\ Y+T_y\\ 1\end{array}\right]$$
• 缩放（scale）
  $$\left[\begin{array}{cccc}{T}_x& 0& 0& \\ 0& T_y& 0& \\ 0& 0& 1& \end{array}\right]\left[\begin{array}{c}X\\ Y\\ 1\end{array}\right]=\left[\begin{array}{c}X\ast T_x\\ Y\ast T_y\\ 1\end{array}\right]$$
• 错切(shear)
  x轴移动
  $$\left[\begin{array}{cccc}1& tan\theta & 0& \\ 0& 1& 0& \\ 0& 0& 1& \end{array}\right]\left[\begin{array}{c}X\\ Y\\ 1\end{array}\right]=\left[\begin{array}{c}X+Y\ast tan\theta \\ Y\\ 1\end{array}\right]$$
  y轴移动
  $$\left[\begin{array}{cccc}1& 0& 0& \\ tan\alpha & 1& 0& \\ 0& 0& 1& \end{array}\right]\left[\begin{array}{c}X\\ Y\\ 1\end{array}\right]=\left[\begin{array}{c}X\\ Y+X\ast tan\alpha \\ 1\end{array}\right]$$
  x、y轴移动
  $$\left[\begin{array}{cccc}1& tan\theta & 0& \\ tan\alpha & 1& 0& \\ 0& 0& 1& \end{array}\right]\left[\begin{array}{c}X\\ Y\\ 1\end{array}\right]=\left[\begin{array}{c}X+Y\ast tan\theta \\ Y+X\ast tan\alpha \\ 1\end{array}\right]$$
  

A = [ a 00 a 01 a 10 a 11 ] B = [ b 00 b 10 ] M = [ A B ] A =

$$\begin{bmatrix} a_{00} & a_{01} \\ a_{10} & a_{11} \\ \end{bmatrix}$$ B= $$\begin{bmatrix} b_{00} \\ b_{10} \\ \end{bmatrix}$$ M= $$\begin{bmatrix} A& B \end{bmatrix}$$ A=[a00​a10​​a01​a11​​]B=[b00​b10​​]M=[A​B​]
$$T=A\ast \left[\begin{array}{c}x\\ y\end{array}\right]+B或者T=M\ast \left[\begin{array}{c}x\\ y\\ 1\end{array}\right]$$
对于图片的每个位置进行转换：
$$T=\left[\begin{array}{c}{a}_{00}\ast x+a_{01}\ast y+b_{00}\\ a_{10}\ast x+a_{11}\ast y+b_{10}\end{array}\right]$$

透视变换与仿射变换

opencv函数使用

什么是光流（optical flow）？

所谓光流即瞬时速度，时间很小时，等同于目标点的位移。
光流的物理意义：光流是由目标物体的运动以及相机的运动，或者二者共同的运动所产生。研究光流场的目的是为了获得运动场。

光流法基本原理

七、 局部配准

• [1]局部配准综述

• [2]仿射变换与透视变换

• [3]kl配准

• [4]配准综述

• [5]配准paperwithcode

• [6]openCV中的findHomography函数分析以及RANSAC算法的详解（源代码分析）

• [7] Python+Opencv2（三）图像特征匹配

-[8]surf特征提取算法