数学学习的瓶颈到底在哪里？到底谁是“学数学的那块料”？

作者：知新_RL | 2024-05-27 21:12:58

踩

我们到底是因为什么而恐惧数学呢？是因为怎么都解答不了的数学题吗？还是理解不了，背不完的数学公式呢？或者是不断“神化”的数学思维？数学学习的瓶颈又到底在哪里呢？谁又是学数学的那块料呢？

如果有一本数学科普书，全书没有一个公式，没有一道数学题目，全都是文字性的语言描述，深入浅出，小学生都能读完，却讲透了数学的本质，那么你是否还会因为书名加了“数学”两字而敬而远之呢？

如果你不相信，不妨读一下《数学的雨伞下：理解世界的乐趣》这本书，从代数、几何到相对论，从温度计到黑洞，作者用简洁而生动的笔触阐释了如何更好地思索、观察与理解世界。

我记得几年前经常合作的一位数学家朋友曾经说过一句话。当时我们俩正要道别，我们决定在两周后的同一天、同一时间再见。在她掏出记事本以便记下见面的日期时，我听到她喃喃低语了一句，多半是说给她自己而不是说给我听的：“今天是 4 月 20 号，那么 14 天之后就是 34 号，那就是 34 减 30——5 月 4 号。”

这个算法让我笑了。我在回程的地铁上想了很长时间，她发明了一个不存在的日期：4 月 34 号。这种思维方式对于一个受过数学训练的人来说既自然又典型！当天晚上，我对几个并非数学专业出身的朋友提出了这个问题：“14 天后是几号？”我发现。他们每一个人推导日期的方式都不一样。有人说，10 天之后是 4 月 30 号，所以 11 天之后就是 5 月 1 号，那么 14 天之后就是 5 月 4 号。从 4 月到 5 月的过渡打破了算术的规则，因为 30 的后面是 1，这一过渡似乎把他们限制在一个数学之外的步骤上去进行月份转换。由于数字的自然增长被打断了，因此必须着意打断这种思维。而我必须承认，如果有人对我提出这个问题，我很可能也会这样推导日期。

相反，我的那位数学家朋友并没有在这些太过实际的障碍上停滞不前。4 月的最后一个日期没有对她的加法形成任何妨碍。因为 20 加14 等于 34，所以日期就会是 4 月 34 号。而 4 月 34 号就等于 5 月 4号，仅此而已（图 2.6）。她发明了一个不存在的日期，以便让自己的推导直达目标。而这丝毫没有妨碍她得到正确的结果！

这是数学颠覆我们三观的优点之一：可以用不存在的东西去恰当地思考。实际上，思考不存在的东西甚至可以说是数学的特性。不存在的东西也就是抽象的东西。

数字显然是最引人注目的例子之一。一旦脱离了被它们模型化的现实，数字就成了纯抽象的概念。它们是想法，是我们用作思维中间环节的想象之物。就像发明 4 月 34 号来推导日期会是方便之法一样，发明新的数字对思考新的问题也会有所帮助。

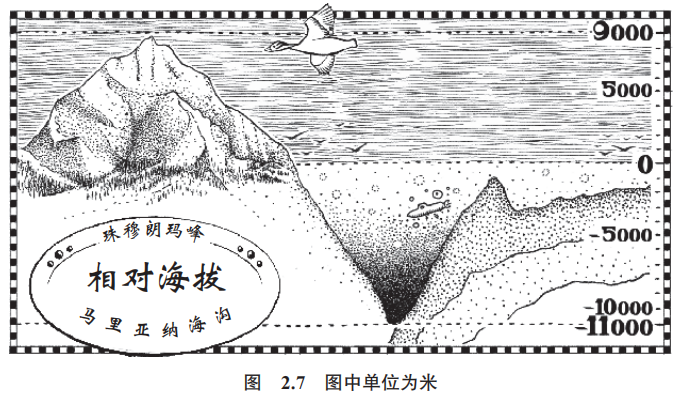
比如，复数就是这样不期而至的。没有任何距离会是 − 11 千米。无论从哪种逻辑上来讲，距离都应该用一个正数来表示。但是，在测量地球上各点之于海平面的海拔时，把位于海平面之下的海渊的海拔看作负数会很实用。照此，位于地壳最深点的马里亚纳海沟的海拔就是约 − 11 千米（图 2.7）。负海拔就是地理学家的 4 月 34 号。

研究数学，就是创造想象的世界，在这些世界中，我们的思维可以自由漫步，不必担心现实的妨碍。这种思维方式虽然涵盖的范围要广得多，但和尼普尔人在加法世界中用来简化乘法的思维方式非常相似。当你碰到一个科学问题时，下面这种解决方法往往会很有效：

1. 创造一个数学世界，你可以在这个世界里把问题模型化；

2. 在这个数学世界里解决问题；

3. 把结果转回到现实世界中。

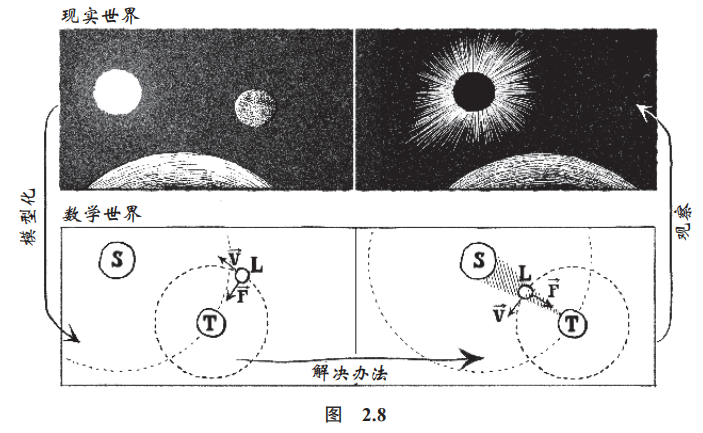
比如说，这种通用的方法就被天文学家用来了解行星的轨迹或预测日食（图 2.8）。

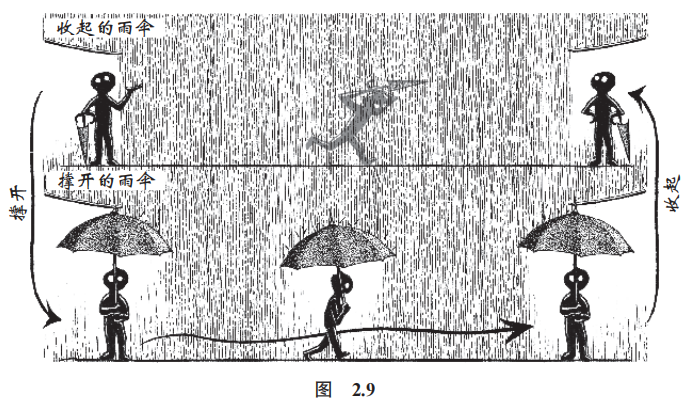
这种解决问题的模式叫作“雨伞定理”。如果你在雨天想要在不被淋湿的情况下从一个地方前往另一个地方，请按照以下步骤操作（图 2.9）：

1. 撑开你的雨伞；

2. 开始你的行程；

3. 收起你的雨伞。

步骤 1 和步骤 3 的操作是相反的，如果你能够在雨伞为你打开的特定世界中达成预期的目标，那么你在操作结束时就会恢复到开始时的状态。负数的雨伞为地理学家测量海拔提供了研究上的便利。对数的雨伞让淹没在乘法中的天文学家得以进入加法的世界。而更广泛地说，抽象的雨伞为所有科学家进入数学世界提供了可能。

在接下来的路途中，我们还会用到很多雨伞。雨伞，是观点的改变，是差异，是从另一个角度看待事物的艺术，一种更适合、更有效的角度。

走得更远，并不总是意味着长久而乏味的努力，而是首先要找到解决所面临的问题的正确方法。如果我们以正确的方式看待问题，那么最错综复杂的问题也会在一瞬间变得简单明了。伟大的智者能尽显其才，首先是因为他们拥有在正确的时间发明正确的雨伞的能力。

在 18 世纪，古怪的作家和旅行家乔纳斯·汉韦（Jonas Hanway）是第一个使用雨伞的伦敦人。这是一把真的雨伞——挡雨的伞。他为此遭受了很多白眼和伦敦马车夫赤裸裸的恶意，因为在当时，搭乘马车一直是在糟糕天气出行而不会被淋湿的唯一方法。毫不畏惧旁人眼光的汉韦继续自豪地使用了三十多年的雨伞，并慢慢看到他的同胞们也开始使用雨伞。在他去世后几个月，第一批商业化雨伞出现在英国，并获得了我们今日所知的成功。

不要惧怕与众不同，这就是雨伞的智慧。让我们无所畏惧，既不感到羞耻，也不抱有偏见。一旦接受在头顶撑起抽象的雨伞并进入数学的世界，我们就不会再全然依赖现实。不必让自己陷在无用的限制或令人尴尬的既有观念之中。你想要一个 4 月 34 号吗？拿去吧！你想要负数吗？拿去吧！你想要无穷吗？拿去吧！如果所有这些想法不会干扰你组织思维，甚至还有所帮助，那为什么要剥夺它们呢？你是自由的！

如此自由，甚至容易让人头晕目眩。在这一点上，数学和一大盘点心有着异曲同工之妙——选择太多，就难以做出选择了。懂得如何在数学世界里自我驾驭，是一种需要实践和直觉的能力。

为此，数学家制造出很多导航工具，其中有两个指南针：一个名叫“实用”，一个名叫“优雅”。“实用”引导我们创造出最贴近现实的抽象世界，在这些抽象世界中进行的研究能够轻松地转化为关于我们宇宙的知识。“优雅”告诉我们要完全抛开现实，并沉醉在抽象世界的奇观中。那里有许许多多美丽的事情要做——如果一件事是无用的，那它就更美了。

每个人都能以自己的方式使用这两个指南针。有些人偏爱其中的某一个，有些人则两个一起用，并不断在两个指南针指示的方向之间寻找完美的平衡。但世界充满奥秘，因此，探索实用之人和探索优雅之人常常会在走过不同的道路之后，在同一个地方不期而遇。看到大自然如此喜爱按照优雅的数学原理运转，真是既让人目瞪口呆，又让人不知所措。

推荐阅读