在做时序预测时，一个显然的思路是：认为离着预测点越近的点，作用越大。比如我这个月体重100斤，去年某个月120斤，显然对于预测下个月体重而言，这个月的数据影响力更大些。假设随着时间变化权重以指数方式下降——最近为0.8，然后0.8**2，0.8**3…，最终年代久远的数据权重将接近于0。将权重按照指数级进行衰减，这就是指数平滑法的基本思想。

指数平滑法有几种不同形式：一次指数平滑法针对没有趋势和季节性的序列，二次指数平滑法针对有趋势但没有季节性的序列，三次指数平滑法针对有趋势也有季节性的序列。“Holt-Winters”有时特指三次指数平滑法。

所有的指数平滑法都要更新上一时间步长的计算结果，并使用当前时间步长的数据中包含的新信息。它们通过”混合“新信息和旧信息来实现，而相关的新旧信息的权重由一个可调整的参数来控制。

产生背景：指数平滑由布朗提出、他认为时间序列的态势具有稳定性或规则性，所以时间序列可被合理地顺势推延；他认为最近的过去态势，在某种程度上会持续的未来，所以将较大的权数放在最近的资料。

基本原理：指数平滑法是移动平均法中的一种，其特点在于给过去的观测值不一样的权重，即较近期观测值的权数比较远期观测值的权数要大。根据平滑次数不同，指数平滑法分为一次指数平滑法、二次指数平滑法和三次指数平滑法等。但它们的基本思想都是：预测值是以前观测值的加权和，且对不同的数据给予不同的权数，新数据给予较大的权数，旧数据给予较小的权数。

方法应用：指数平滑法是生产预测中常用的一种方法。也用于中短期经济发展趋势预测，所有预测方法中，指数平滑是用得最多的一种。

指数平滑法的基本公式是：

式中，

St--时间t的平滑值；
yt--时间t的实际值；
St − 1--时间t-1的平滑值；
a--平滑常数，其取值范围为[0,1]；

由该公式可知：

St 是 yt 和 St − 1 的加权算数平均数，随着 a 取值的大小变化，决定 yt 和 St − 1 对 St 的影响程度，当a取1时，St = yt；当a取0时，St = St − 1。
St具有逐期追溯性质，可探源至St − t + 1为止，包括全部数据。其过程中，平滑常数以指数形式递减，故称之为指数平滑法。指数平滑常数取值至关重要。平滑常数决定了平滑水平以及对预测值与实际结果之间差异的响应速度。平滑常数a越接近于1，远期实际值对本期平滑值影响程度的下降越迅速；平滑常数a越接近于 0，远期实际值对本期平滑值影响程度的下降越缓慢。由此，当时间数列相对平稳时，可取较大的a；当时间数列波动较大时，应取较小的a，以不忽略远期实际值的影响。生产预测中，平滑常数的值取决于产品本身和管理者对良好响应率内涵的理解。
尽管St包含有全期数据的影响，但实际计算时，仅需要两个数值，即 yt 和 St − 1，再加上一个常数a，这就使指数滑动平均具逐期递推性质，从而给预测带来了极大的方便。
根据公式 $S_1=a\cdot y_1+(1-a)S_0$ ，当欲用指数平滑法时才开始收集数据，则不存在y0。无从产生S0，自然无法据指数平滑公式求出S1，指数平滑法定义S1为初始值。初始值的确定也是指数平滑过程的一个重要条件。

　　如果能够找到y1以前的历史资料，那么，初始值S1的确定是不成问题的。数据较少时可用全期平均、移动平均法；数据较多时，可用最小二乘法。但不能使用指数平滑法本身确定初始值，因为数据必会枯竭。

　　如果仅有从y1开始的数据，那么确定初始值的方法有：

　　1）取S1等于y1；

　　2）待积累若干数据后，取S1等于前面若干数据的简单算术平均数，如：S1=（y1+ y2+y3）/3等等。

2 一次指数平滑预测（又叫简单指数平滑，simple exponential smoothing， SES）

2.1 定义

当时间数列无明显的趋势变化，可用一次指数平滑预测。其预测公式为：

式中， $y_{t+1}^\prime$ 为 t + 1 期的预测值，即本期（t 期）的平滑值St； yt为 t 期的实际值； $y_{t}^\prime$ 为 t 期的预测值，即上期的平滑值St − 1 。

该公式又可以写作： $y_{t+1}^\prime = y_{t} + a (y^{t}-y_{t}^\prime)$ 。可见，下期预测值又是本期预测值与以a为折扣的本期实际值与预测值误差之和。

初始值y1和y2一般设为y1。或者y1定为前三个数的平均值。

可以看出，在指数平滑法中，所有先前的观测值都对当前的平滑值产生了影响，但它们所起的作用随着参数的幂的增大而逐渐减小。那些相对较早的观测值所起的作用相对较小。同时，称 α 为记忆衰减因子可能更合适——因为 α 的值越大，模型对历史数据“遗忘”的就越快。从某种程度来说，指数平滑法就像是拥有无限记忆（平滑窗口足够大）且权值呈指数级递减的移动平均法。

α的选择：

一次指数平滑所得的计算结果可以在数据集及范围之外进行扩展，因此也就可以用来进行预测。预测方式为：

是最后一个已经算出来的值。h等于1代表预测的下一个值。即一次指数平滑预测的未来多个值都是相等的。

2.2 例题

已知某种产品最近15个月的销售量如下表所示：

用一次指数平滑值预测下个月的销售量y16。

为了分析加权系数a的不同取值的特点，分别取a=0.1，a=0.3，a=0.5 计算一次指数平滑值，并设初始值为最早的三个数据的平均值，以a = 0.5的一次指数平滑值计算为例，有

计算得到下表：

按上表可得时间15月对应的19.9 26.2 28.1可以分别根据预测公式来预测第16个月的销售量。

以a = 0.5为例：

由上述例题可得结论：

指数平滑法对实际序列具有平滑作用，权系数（平滑系数）a 越小，平滑作用越强，但对实际数据的变动反应较迟缓。
在实际序列的线性变动部分，指数平滑值序列出现一定的滞后偏差的程度随着权系数（平滑系数）a 的增大而减少，但当时间序列的变动出现直线趋势时，用一次指数平滑法来进行预测仍将存在着明显的滞后偏差。因此，也需要进行修正。修正的方法也是在一次指数平滑的基础上再进行二次指数平滑，利用滞后偏差的规律找出曲线的发展方向和发展趋势，然后建立直线趋势预测模型，故称为二次指数平滑法。

3 二次指数平滑法（Holt’s linear trend method）

3.1 定义

1） a为加权系数；

2）指数平滑法对实际序列具有平滑作用，权系数（平滑系数）越小，平滑作用越强，但是对实际数据的变动反映较迟缓；

3）在实际序列的线性变动部分，指数平滑值序列出现一定的滞后偏差的程度随着权系数(平滑系数)的增大而减少；但当时间序列的变动出现直线趋势时，用一次指数平滑法来进行预测仍将存在着明显的滞后偏差。因此，也需要进行修正。

4）修正的方法也是在一次指数平滑的基础上再进行二次指数平滑，利用滞后偏差的规律找出曲线的发展方向和发展趋势，然后建立直线趋势预测模型，故称为二次指数平滑法。

在一次指数平滑的基础上得二次指数平滑的计算公式为：

式中：

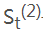——第t周期的二次指数平滑值；
——第t周期的一次指数平滑值；
——第t-1周期的二次指数平滑值；
a ——加权系数（也称为平滑系数）。

二次指数平滑法是对一次指数平滑值作再一次指数平滑的方法。它不能单独地进行预测，必须与一次指数平滑法配合，建立预测的数学模型，然后运用数学模型确定预测值。

二次指数平滑数学模型：

3.2 例题

（1）某地1983年至1993年财政入的资料如下，试用指数平滑法求解趋势直线方程并预测1996年的财政收入

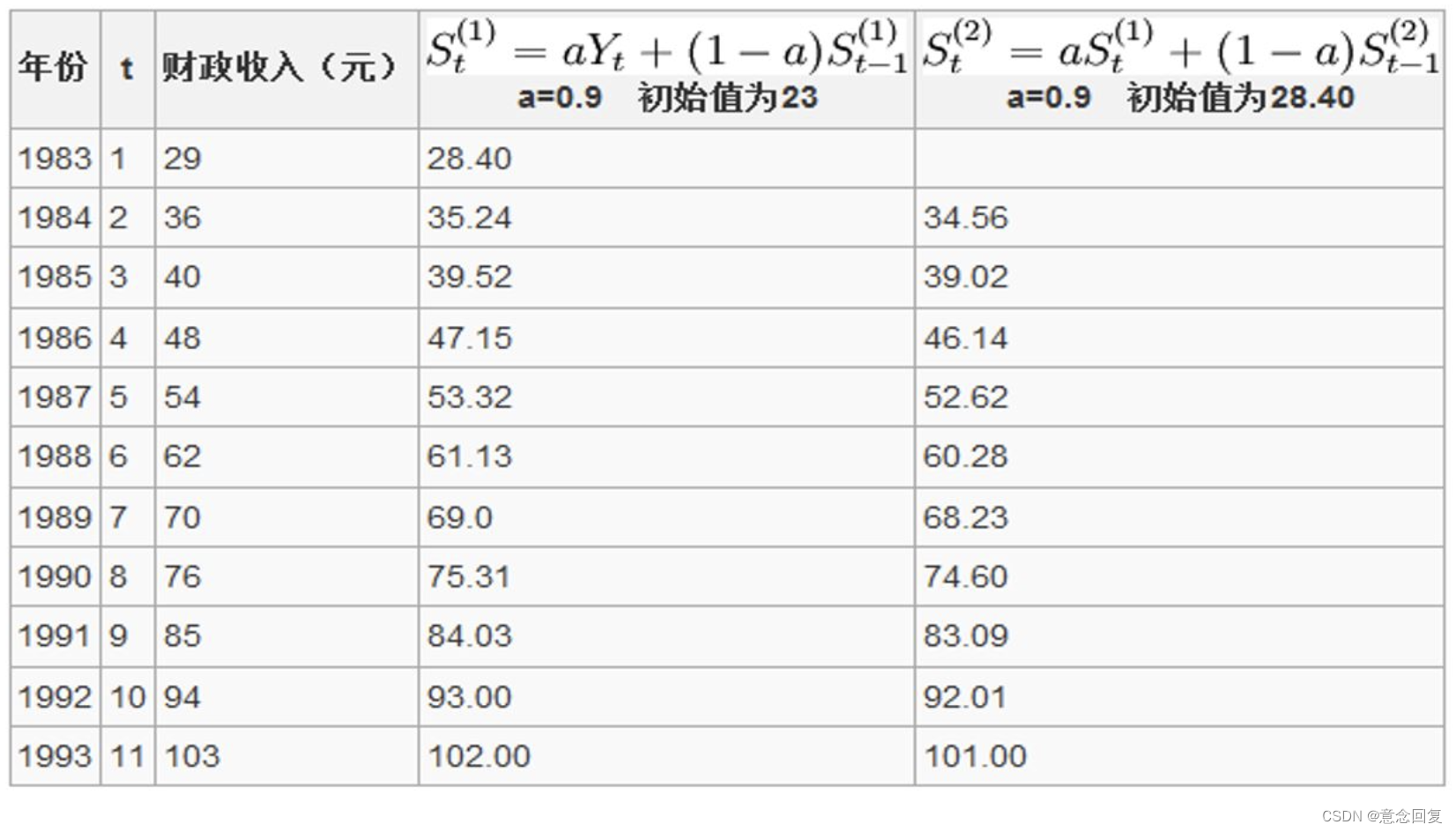
（2）已知某厂1978～1998年的钢产量如下表所示，试预测1999年、2000年该厂的钢产量。（用excel如何实现平滑指数）

根据二次平滑指数数学模型进行计算a、b值。

得到趋势线预测模型：y=3994.9+141.2T，从而可以计算出：

y1999=3994.9+141.2*1=4136.14

y2000=3994.9+141.2*2= 4277.34

4 三次指数平滑预测（Holt-Winters’ seasonal method）

4.1 定义

若时间序列的变动呈现出二次曲线趋势，则需要采用三次指数平滑法进行预测。三次指数平滑是在二次指数平滑的基础上再进行一次平滑，其计算公式为：

三次指数平滑法的预测模型为：

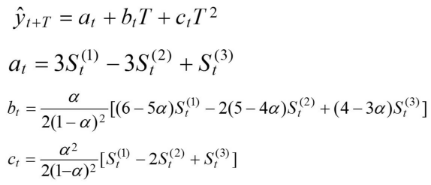
4.2 例题

我国某种耐用消费品1996年至2006年的销售量如表所示，试预测2007、2008年的销售量。

三次指数平滑的计算表：

解：通过实际数据序列呈非线性递增趋势，采用三次指数平滑预测方法。解题步骤如下。确定指数平滑的初始值和权系数（平滑系数）a。设一次、二次指数平滑的初始值为最早三个数据的平均值，即

实际数据序列的倾向性变动较明显，权系数（平滑系数）a 不宜取太小，故取a= 0.3。

根据指数平滑值计算公式依次计算一次、二次、三次指数平滑值：

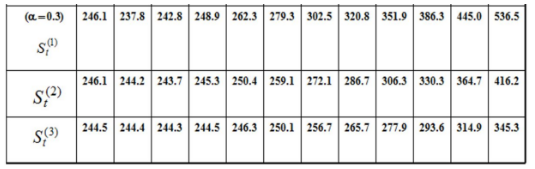
计算非线性预测模型的系数at,bt,ct。目前周期数t = 11，将表中的有关数据代入式后分别得

建立非线性预测模型。将各系数代入式（1-18）得

预测2007年和2008年的产品销售量。2007年，其预测超前周期为T = 1；2008年，其预测超前周期为T = 2。代入模型，得

于是得到2007年的产品销售量的预测值为809万台，2008年的产品销售量的预测值为920万台。预测人员可以根据市场需求因素的变动情况，对上述预测结果进行评价和修正。

5 加权系数a的选择

在指数平滑法中，预测成功的关键是 a 的选择。a 的大小规定了在新预测值中新数据和原预测值所占的比例。a 值愈大，新数据所占的比重就愈大，原预测值所占比重就愈小，反之亦然。

理论界一般认为有以下方法可供选择：

经验判断法。这种方法主要依赖于时间序列的发展趋势和预测者的经验做出判断。

1、当时间序列呈现较稳定的水平趋势时，应选较小的α值，一般可在0.05～0.20之间取值；

2、当时间序列有波动，但长期趋势变化不大时，可选稍大的α值，常在0.1～0.4之间取值；

3、当时间序列波动很大，长期趋势变化幅度较大，呈现明显且迅速的上升或下降趋势时，宜选择较大的α值，如可在0.6～0.8间选值，以使预测模型灵敏度高些，能迅速跟上数据的变化；

4、当时间序列数据是上升（或下降）的发展趋势类型，α应取较大的值，在0.6~1之间。

试算法。根据具体时间序列情况，参照经验判断法，来大致确定额定的取值范围，然后取几个α值进行试算，比较不同α值下的预测标准误差，选取预测标准误差最小的α。

在实际应用中预测者应结合对预测对象的变化规律做出定性判断且计算预测误差，并要考虑到预测灵敏度和预测精度是相互矛盾的，必须给予二者一定的考虑，采用折中的α值。

指数平滑法的缺点：

对数据的转折点缺乏鉴别能力，但这一点可通过调查预测法或专家预测法加以弥补。
长期预测的效果较差，故多用于短期预测。

指数平滑法的优点：

对不同时间的数据的非等权处理较符合实际情况。
实用中仅需选择一个模型参数a 即可进行预测，简便易行。
具有适应性，也就是说预测模型能自动识别数据模式的变化而加以调整。

6 Holt Winter线性和季节性指数平滑法

6.1 Holt Winter线性指数平滑法

Holt Winter线性指数平滑法本质上就是二次指数平滑法，可以预测具有趋势的时间序列。

霍尔特扩展简单指数平滑方法，允许有趋势的数据预测。它只适用于两个等级（多个序列的平均值）和趋势的指数平滑方法。用数学符号表示，现在需要三个等式：一个用于等级，一个用于趋势，一个结合等级与得到预测值Ŷ的趋势：

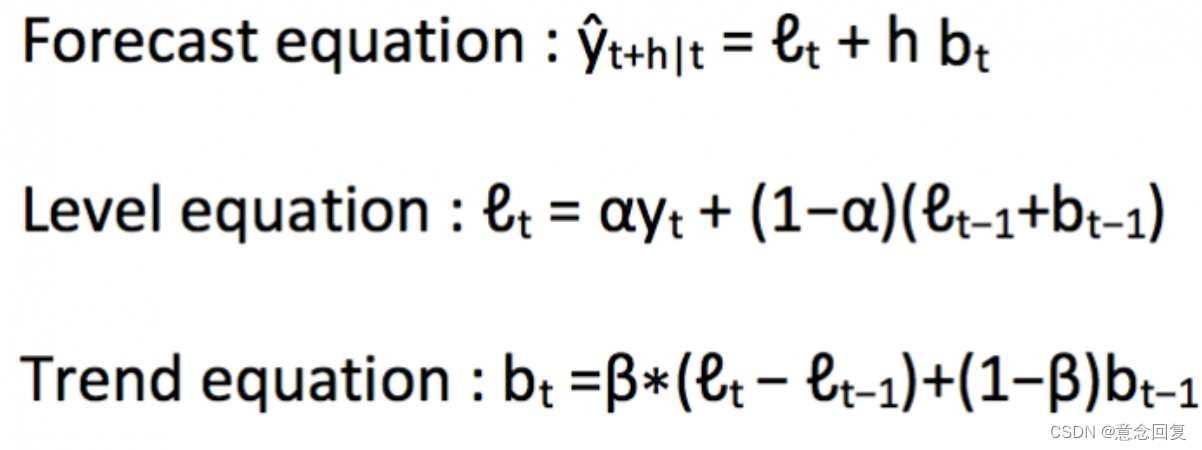
我们在上述算法中预测的值称为等级。在上面的三个等式中，可以注意到我们增加了等级和趋势来生成预测等式。

作为简单指数平滑法，这里的等级等式表明它是一个观察数的加权平均值和样本内前步预测。趋势等式表明，这是一个基于ℓ(t)−ℓ(t−1)和和b（t−1）的时间t的预测趋势的加权平均值。

我们将添加这些等式来生成预测等式。也可以通过乘以趋势和等级而不是增加，来生成乘法预测等式。当趋势呈线性上升或下降时，则采用加法等式，而当趋势呈指数下降时，则采用乘法等式。实践表明乘法是一种更稳定的预测，但加性方法更容易理解。

6.2 Holt Winter季节性指数平滑法

Holt Winter季节性指数平滑本质上就是三次指数平滑法，添加了一个新的参数p来表示平滑后的趋势。

当一个序列在每个固定的时间间隔中都出现某种重复的模式，就称之具有季节性特征，而这样的一个时间间隔称为一个季节(理解：比如说在一个周内，销量呈现出重复的模式)。

一个季节的长度k为它所包含的序列点个数。

二次指数平滑考虑了序列的baseline和趋势，三次就是在此基础上增加了一个季节分量。类似于趋势分量，对季节分量也要做指数平滑。比如预测下一个季节第3个点的季节分量时，需要指数平滑地考虑当前季节第3个点的季节分量、上个季节第3个点的季节分量...等等。详细的有下述公式(累加法)：

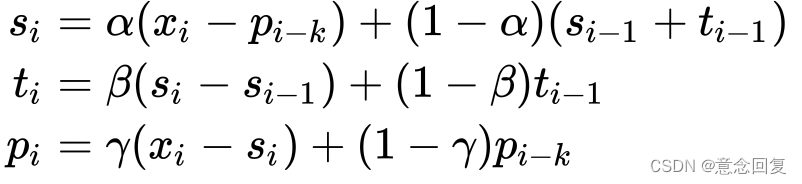
其中，是指“周期性”部分。

预测公式如下：

是这个周期的长度。

7 python实现

7.1 一次指数平滑


import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.holtwinters import SimpleExpSmoothing
 
x1 = np.linspace(0, 1, 100)
y1 = pd.Series(np.multiply(x1, (x1 - 0.5)) + np.random.randn(100))
ets1 = SimpleExpSmoothing(y1)
r1 = ets1.fit()
pred1 = r1.predict(start=len(y1), end=len(y1) + len(y1)//2)
 
pd.DataFrame({
    'origin': y1,
    'fitted': r1.fittedvalues,
    'pred': pred1
}).plot(legend=True)
plt.show()

7.2 二次指数平滑


import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
 
from statsmodels.tsa.holtwinters import Holt
 
x2 = np.linspace(0, 99, 100)
y2 = pd.Series(0.1 * x2 + 2 * np.random.randn(100))
ets2 = Holt(y2)
r2 = ets2.fit()
pred2 = r2.predict(start=len(y2), end=len(y2) + len(y2)//2)
 
pd.DataFrame({
    'origin': y2,
    'fitted': r2.fittedvalues,
    'pred': pred2
}).plot(legend=True)
plt.show()

7.3 三次指数平滑

无趋势：


import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
 
from statsmodels.tsa.holtwinters import ExponentialSmoothing
 
x3 = np.linspace(0, 4 * np.pi, 100)
y3 = pd.Series(20 + 8 * np.cos(2 * x3) + 2 * np.random.randn(100))
ets3 = ExponentialSmoothing(y3, trend=None, seasonal='add', seasonal_periods=25)
r3 = ets3.fit()
pred3 = r3.predict(start=len(y3), end=len(y3) + len(y3)//2)
 
pd.DataFrame({
    'origin': y3,
    'fitted': r3.fittedvalues,
    'pred': pred3
}).plot(legend=True)
plt.show()

累加：


import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
 
from statsmodels.tsa.holtwinters import ExponentialSmoothing
 
x3 = np.linspace(0, 4 * np.pi, 100)
y3 = pd.Series(20 + 0.1 * np.multiply(x3, x3) + 8 * np.cos(2 * x3) + 2 * np.random.randn(100))
ets3 = ExponentialSmoothing(y3, trend='add', seasonal='add', seasonal_periods=25)
r3 = ets3.fit()
pred3 = r3.predict(start=len(y3), end=len(y3) + len(y3)//2)
 
pd.DataFrame({
    'origin': y3,
    'fitted': r3.fittedvalues,
    'pred': pred3
}).plot(legend=True)
plt.show()

累乘：


import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
 
from statsmodels.tsa.holtwinters import ExponentialSmoothing
 
x3 = np.linspace(0, 4 * np.pi, 100)
y3 = pd.Series(20 + 0.1 * np.multiply(x3, x3) + 8 * np.cos(2 * x3) + 2 * np.random.randn(100))
ets3 = ExponentialSmoothing(y3, trend="multiplicative", seasonal='add', seasonal_periods=25)
r3 = ets3.fit()
pred3 = r3.predict(start=len(y3), end=len(y3) + len(y3)//2)
 
pd.DataFrame({
    'origin': y3,
    'fitted': r3.fittedvalues,
    'pred': pred3
}).plot(legend=True)
plt.show()

https://www.jianshu.com/p/2c607fe926f0

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/笔触狂放9/article/detail/132394