改善神经网络——优化算法（mini-batch、动量梯度下降法、Adam优化算法）_动量梯度下降优化

优化算法可以使神经网络运行的更快，机器学习的应用是一个高度依赖经验的过程，伴随着大量迭代的过程，你需要训练诸多模型，才能找到合适的那一个，所以，优化算法能够帮助你快速训练模型。

其中一个难点在于，深度学习没有在大数据领域发挥最大的效果，我们可以利用一个巨大的数据集来训练神经网络，而在巨大的数据集基础上进行训练速度很慢。因此，你会发现，使用快速的优化算法，使用好用的优化算法能够大大提高你和团队的效率

梯度下降

在机器学习中，最简单就是没有任何优化的梯度下降(GD,Gradient Descent)，我们每一次循环都是对整个训练集进行学习，这叫做批量梯度下降(Batch Gradient Descent)，参考文章 机器学习——梯度下降算法。

使用梯度下降算法时，假设对 m 个样本进行计算，把训练样本放大巨大的矩阵 $X$ 当中去，$X=[x^{(1)}{x}^{(2)}{x}^{(3)}...x^{(m)}]$ ，$Y$ 也是如此，$Y=[y^{(1)}{y}^{(2)}{y}^{(3)}...y^{(m)}]$ ，向量化能够让你相对较快地处理所有 m 个样本。如果 m 很大的话，处理速度仍然缓慢。比如说，如果 m 是500万或5000万或者更大的一个数，在对整个训练集执行梯度下降法时，你要做的是，你必须处理整个训练集，然后才能进行一步梯度下降法，然后你需要再重新处理500万个训练样本，才能进行下一步梯度下降法。所以如果你在处理完整个500万个样本的训练集之前，先让梯度下降法处理一部分，你的算法速度会更快。

Mini-batch 梯度下降（Mini-batch Gradient Descent）

把训练集分割为小一点的子集训练，这些子集被取名为mini-batch。

梯度下降算法演变来的有随机梯度下降（SGD）算法和小批量梯度下降算法（Mini-batch Gradient Descent）。随机梯度下降相当于小批量梯度下降，但是和mini-batch不同的是其中每个小批量(mini-batch)仅有1个样本，和梯度下降不同的是你一次只能在一个训练样本上计算梯度，而不是在整个训练集上计算梯度。

在随机梯度下降中，在更新梯度之前，只使用1个训练样本。 当训练集较大时，随机梯度下降可以更快，但是参数会向最小值摆动，而不是平稳地收敛，我们来看一下比较图:

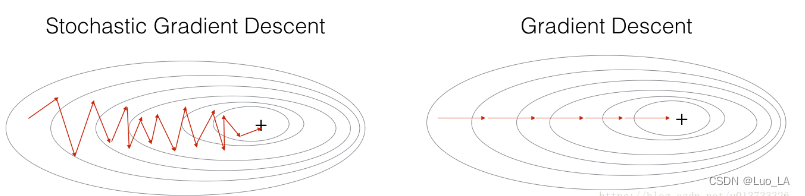
在实际中，更好的方法是使用小批量(mini-batch)梯度下降法，小批量梯度下降法是一种综合了梯度下降法和随机梯度下降法的方法，在它的每次迭代中，既不是选择全部的数据来学习，也不是选择一个样本来学习，而是把所有的数据集分割为一小块一小块的来学习，它会随机选择一小块（mini-batch），块大小一般为2的n次方倍。

假设每一个子集中只有1000个样本，那么把其中的 $x^{(1)}$到$x^{(1000)}$ 取出来，将其称为第一个子训练集，也叫做mini-batch，然后你再取出接下来的1000个样本，从 $x^{(1001)}$到$x^{(2000)}$ ，然后再取1000个样本，以此类推。

假设训练样本 m = 500万，每个mini-batch 都有1000个样本，也就是说，有5000个mini-batch。把$x^{(1)}$到$x^{(1000)}$ 称为 X { 1 } X^{\{1\}} X{1}，$x^{(1001)}$到$x^{(2000)}$ 称为 X { 2 } X^{\{2\}} X{2}，以此类推直到 $X^{(5000)}$， 对 $Y$ 进行同样的处理。mini-batch的数量 t 组成了 X { t } X^{\{t\}} X{t}， Y { t } Y^{\{t\}} Y{t}。 X { t } X^{\{t\}} X{t}的维数是$(n_x,1000)$，$n_x$ 是样本输入单元个数， Y { t } Y^{\{t\}} Y{t} 的维数是$(1,1000)$

之前我们使用了上角小括号 ( i ) 表示训练集里的值，所以 $x^{(i)}$是第 i 个训练样本。我们用了上角中括号 [ l ] 来表示神经网络的层数， $z^{[l]}$ 表示神经网络中第 l 层的 z 值，我们现在引入了大括号 t 来代表不同的 mini-batch，所以我们有 X { t } X^{\{t\}} X{t}， Y { t } Y^{\{t\}} Y{t}。

在训练集上运行mini-batch梯度下降法，你运行for t=1……5000，因为我们有5000个各有1000个样本的组，在for循环里你要做得基本就是对 X { t } X^{\{t\}} X{t} 和 Y { t } Y^{\{t\}} Y{t} 执行一步梯度下降法。

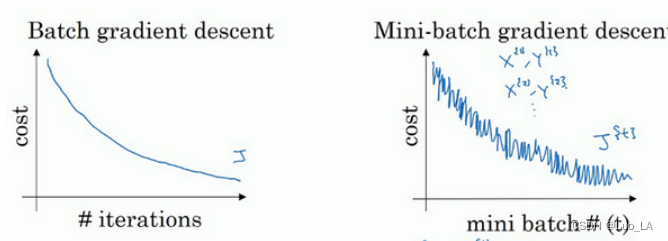
使用batch梯度下降法时，每次迭代都需要历遍整个训练集，可以预期每次迭代成本都会下降，所以如果成本函数 J 是迭代次数的一个函数，它应该会随着每次迭代而减少，如果 J 在某次迭代中增加了，那肯定出了问题，也许你的学习率太大。

使用mini-batch梯度下降法，如果你作出成本函数在整个过程中的图，则并不是每次迭代都是下降的，特别是在每次迭代中，你要处理的是 X { t } X^{\{t\}} X{t} 和 Y { t } Y^{\{t\}} Y{t} ，作出成本函数 J { t } J^{\{t\}} J{t} 的图只和 X { t } X^{\{t\}} X{t} ， Y { t } Y^{\{t\}} Y{t} 有关，成本函数 J 的图的结果走向朝下，但有更多的噪声。这是因为每次迭代下你都在训练不同的样本集或者说训练不同的mini-batch。

使用mini-batch梯度下降法时，需要决定的变量之一是mini-batch的大小， m 就是训练集的大小，极端情况下，如果mini-batch的大小等于 m ，其实就是batch梯度下降法；假设mini-batch大小为1，就是随机梯度下降法。

在随机梯度下降法中，从某一点开始，我们重新选取一个起始点，每次迭代，你只对一个样本进行梯度下降，大部分时候你向着全局最小值靠近，有时候你会远离最小值，因为那个样本恰好给你指的方向不对，因此随机梯度下降法是有很多噪声的，平均来看，它最终会靠近最小值，不过有时候也会方向错误，因为随机梯度下降法永远不会收敛，而是会一直在最小值附近波动，但它并不会在达到最小值并停留在此。

另外，随机梯度下降法的一大缺点是，你会失去所有向量化带给你的加速，因为一次性只处理了一个训练样本，这样效率过于低下，所以实践中最好选择不大不小的mini-batch尺寸，实际上学习率达到最快。一方面，你得到了大量向量化，如果mini-batch大小为1000个样本，你就可以对1000个样本向量化，比你一次性处理多个样本快得多。另一方面，你不需要等待整个训练集被处理完就可以开始进行后续工作。

指数加权平均

指数加权平均值，也被称为移动平均值，从名字可以看出来它其实也是一种求平均值的算法，在后面介绍动量、RMSProp和Adam的时候都需要用到它。

计算
指数加权平均计算公式：
$$v_t=\beta v_{t-1}+(1-\beta ){\theta }_t$$
其中$\beta$指的是系数通常取0.9，$v_n$ 表示的是当前的指数加权平均值，$\theta$表示的是当前的值。下面用一个例子来介绍。

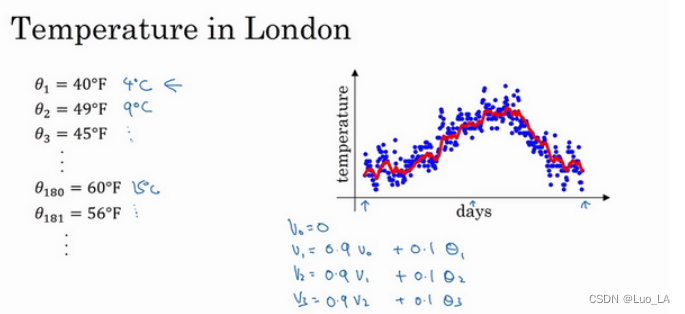
如上图是某年英国伦敦一年的温度散点图，用该数据计算温度的移动平均值。
你要做的是，首先使 $v_0=0$， 每天，需要使用0.9的加权数之前的数值加上当日温度的0.1倍，即 $v_1=0.9v_0+0.1{\theta }_1$，所以这里是第一天的温度值。

第二天，又可以获得一个加权平均数，0.9乘以之前的值加上当日的温度0.1倍，即 $v_2=0.9v_0+0.1{\theta }_2$，以此类推。

如此计算，然后用红线作图，便得到如下图所示的结果。

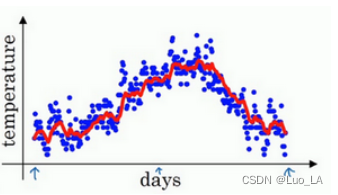
在计算时，可视 $v_t$ 大概是 $\frac{1}{1-\beta }$ 的每日平均温度，如果$\beta$是0.9，$v_t$将是十天的平均值，也就是上图红心部分。

如果将$\beta$设置为接近1的一个值，比如0.98，计算 $\frac{1}{1-0.98}=50$ ，这就是粗略平均了一下过去50天的温度，作图得到下图所示的绿线。

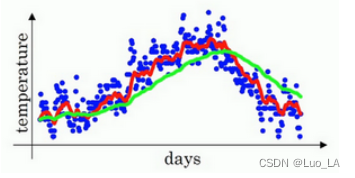
对于 $\beta =0.98$ 时，要注意几点，你得到的曲线要平坦一些，原因在于你多平均了几天的温度，所以这个曲线，波动更小，更加平坦，缺点是曲线进一步右移，因为现在平均的温度值更多，要平均更多的值，指数加权平均公式在温度变化时，适应地更缓慢一些，所以会出现一定延迟，因为当 $\beta =0.98$ ，相当于给前一天的值加了太多权重，只有0.02的权重给了当日的值，所以温度变化时，温度上下起伏，当 $\beta$ 较大时，指数加权平均值适应地更缓慢一些。

如果将$\beta$设置为0.5， 将只平均了两天的温度。

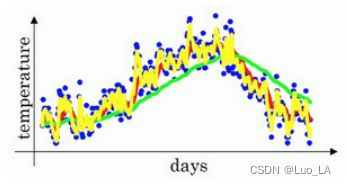
由于仅平均了两天的温度，平均的数据太少，所以得到的曲线有更多的噪声，有可能出现异常值，但是这个曲线能够更快适应温度变化。

通过调整这个参数（$\beta$ 在后面的学习算法中将是一个很重要的参数），可以取得稍微不同的效果，往往中间有某个值效果最好， $\beta$ 为中间值时得到的红色曲线，比起绿线和黄线更好地平均了温度。

指数加权平均数公式的好处之一在于，它占用极少内存，电脑内存中只占用一行数字而已，然后把最新数据代入公式，不断覆盖就可以了，正因为这个原因，其效率，它基本上只占用一行代码，计算指数加权平均数也只占用单行数字的存储和内存。

偏差修正

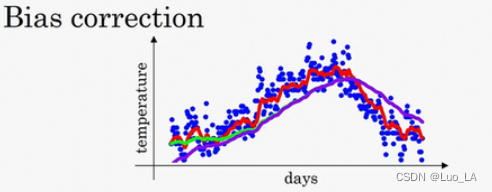
在实际的计算过程中，在 $\beta$ 等于 0.98 的时候，得到的并不是绿色曲线，而是紫色曲线，你可以注意到紫色曲线的起点较低。这是因为在计算移动平均数的时候，初始化 $v_0=0$，$v_1=0.9v{8}_0+0.02{\theta }_1$，但是$v_0=0$，所以计算得 $v_1=0.02{\theta }_1$，因此得到得值会小很多，第一天温度的估测是不准的，同样代入$v_2$得计算公式，$v_2$也不能很好得估测出这一年得前两天的温度。

有个办法可以修改这一估测，让估测变得更好，更准确，特别是在估测初期，也就是不用 $v_t$ ，而是用$\frac{v_t}{1-{\beta }^t}$。

举个例子，当 $t=2$时，$1-{\beta }^t=1-0.98^2=0.0396$，因此对第二天温度的估测变成了$\frac{v_2}{0.0396}=\frac{0.0196{\theta }_1+0.02{\theta }_2}{0.0396}$，也就是${\theta }_1$ 和 ${\theta }_2$的加权平均数，并去除了偏差。你会发现随着 $t$ 增加，${\beta }^t$ 接近于0，所以当 $t$ 很大的时候，偏差修正几乎没有作用，因此当 $t$ 较大的时候，紫线基本和绿线重合了。

包含动量的梯度下降

在普通的梯度下降中，如果遇到了比较复杂的情况，就会出现：如果学习率过大，摆动过大，误差较大；如果学习率过小，又会使得迭代次数增加，学习时间会很长。在神经网络模型中就常常会遇到上面这些情况，总是会出现解一种在小范围震荡而很难达到最优解的情况。

而动量梯度则可以比较好的避免上述问题。它的过程类似于一个有质量的小球在函数曲线上向下滚落。当球滚到最低点后，由于具有惯性还会继续上升一段，然后再滚落回来，再经过最低点上去…最终小球就停留到最低点处。而且由于小球具有惯性这一点，当函数曲线或曲面比较陡峭复杂时，它便可以越过这些而尽快地达到最低点。

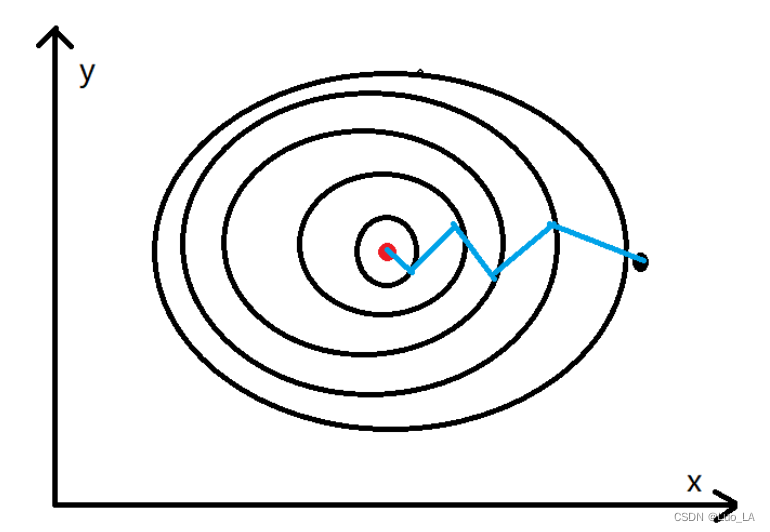
动量梯度下降算法在梯度下降算法的基础上做了一些优化，梯度下降算法的收敛如下图所示。

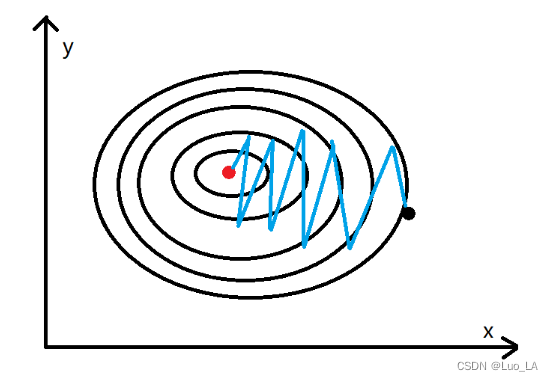
其中黑点表示的是起点，红点表示的是终点。通过梯度下降算法不停的迭代，慢慢的从黑点移动到红点的位置，通过上图可以发现黑点的移动轨迹在y方向上一直存在上下波动，而这个对于黑点移动到红点的位置没有任何的帮助，反而是在浪费时间，因为我们更希望减少这种不必要的计算，加速x轴方向上的移动步伐，如下图所示

实现
梯度下井算法的参数更新公式：
$w=w-\alpha \ast dw$
$b=b-\alpha \ast db$
动量梯度下降算法参数更新公式：
$v_w=\beta v_w+(1-\beta )dw$
$v_b=\beta v_b+(1-\beta )db$
$w=w-\alpha \ast v_w$
$b=b-\alpha \ast v_b$

上式中 $\alpha$ 表示学习率，通过上式可以发现，动量梯度下降算法在更新参数的时候并不是直接使用的梯度，它还利用到以前的梯度，具体到多少，与 $\beta$ 的大小有关，$\beta$ 越大使用到以前的梯度越多，$\beta$ 越小使用到以前的梯度越小。

因为在y轴方向上梯度是有正有负的，所以均值就近似为0，即在y轴方向上不会有太大的变化。而x轴方向上的梯度都是一致的，所以能够为x轴方向上提供动量加速更新。由于动量梯度下降算法，在更新参数的时候不仅使用到了当前的梯度还使用到了以前梯度的均值作为动量，当陷入到局部极小值(梯度接近于0)，在更新的时候动量梯度下降算法还可以利用以前梯度的均值来跳出局部极小值，而梯度下降算法只会陷入到局部极小值。

RMSprop算法

RMSprop算法全称root mean square prop，RMSprop算法的思想和Moment算法的思想是一致的都是通过减少在y轴方向上的抖动，加大x轴方向上的移动步长。而在实现上略有不同，Moment主要是利用累积以前的梯度来实现加速，而RMSprop算法的思想是利用梯度下降算法在y轴方向上的梯度比较大，而在x轴方向上的梯度相对较小。在进行参数更新的时候，让y轴方向上的梯度（$db$）除以一个大的数，这样y轴更新的幅度就小。而x轴方向上的梯度（$dw$）除以一个小的数，这样x轴更新的幅度就大。从而实现了，减小了y轴方向上的更新步长，增大了x轴方向上的更新步长，使得算法能够更快的收敛。更新公式如下：

$S_{dw}=\beta S_{dw}+(1-\beta )d{w}^2$
$S_{db}=\beta S_{db}+(1-\beta )d{b}^2$
$w=w-\alpha \ast \frac{dw}{\sqrt{S_{dw}}+\epsilon }$
$b=b-\alpha \ast \frac{dw}{\sqrt{S_{db}}+\epsilon }$

为了避免在更新参数的时候，分母为0，所以需要在分母上加上一个极小的数$\epsilon$，通常取$10^{-8}$。$d{w}^2$ 表示的是参数 $w$ 的梯度的平方也称为微分的平方。

把纵轴和横轴方向分别称为 $b$ 和 $w$ ，只是为了方便展示而已。实际中，你会处于参数的高维度空间，所以需要消除摆动的垂直维度，你需要消除摆动，实际上是参数 $w_1，w_2$ 等的合集，水平维度可能 $w_3，w_4$ 等等，因此把 $b$ 和 $w$ 分开只是方便说明。实际中 $dw$ 是一个高维度的参数向量， $db$ 也是一个高维度参数向量。

Adam算法

Adam算法全称Adaptive Moment Estimation，主要是结合了Moment算法和RMSprop算法。公式如下：

$v_{dw}=0,v_{db}=0,S_{dw}=0,S_{db}=0$
$v_{dw}={\beta }_1{v}_{dw}+(1-{\beta }_1)dw$
$v_{db}={\beta }_1{v}_{db}+(1-{\beta }_1)db$
$S_{dw}={\beta }_2{S}_{dw}+(1-\beta )d{w}^2$
$S_{db}={\beta }_2{S}_{db}+(1-\beta )d{b}^2$

参数更新：

$w=w-\alpha \ast \frac{v_{dw}}{\sqrt{S_{dw}}+\epsilon }$
$b=b-\alpha \ast \frac{v_{db}}{\sqrt{S_{db}}+\epsilon }$

在使用指数加权平均值算法的时候，可能存在初始化的偏差比较大的情况，可以通过下面的方法进行偏差修正：

$v_{dw}^{corrected}=\frac{v_{dw}}{1-{\beta }_1^t}$， $v_{db}^{corrected}=\frac{v_{db}}{1-{\beta }_1^t}$

$S_{dw}^{corrected}=\frac{S_{dw}}{1-{\beta }_2^t}$， $S_{db}^{corrected}=\frac{S_{db}}{1-{\beta }_2^t}$

$w=w-\alpha \ast \frac{v_{dw}^{corrected}}{\sqrt{S_{dw}^{corrected}}+\epsilon }$，$b=b-\alpha \ast \frac{v_{db}^{corrected}}{\sqrt{S_{db}^{corrected}}+\epsilon }$

上式中 $t$ 表示迭代次数，${\beta }_1$ 是Momentum的超参数通常取0.9，${\beta }_2$ 是RMSprop的超参数通常取0.999，$\epsilon$ 是用来避免分母为0的情况取 $10^{-8}$。

参考文章
https://blog.csdn.net/weixin_36815313/article/details/105432576
https://blog.csdn.net/sinat_29957455/article/details/88088720