FPGA实现图像处理之【直方图均衡-寄存器版】

FPGA实现直方图统计

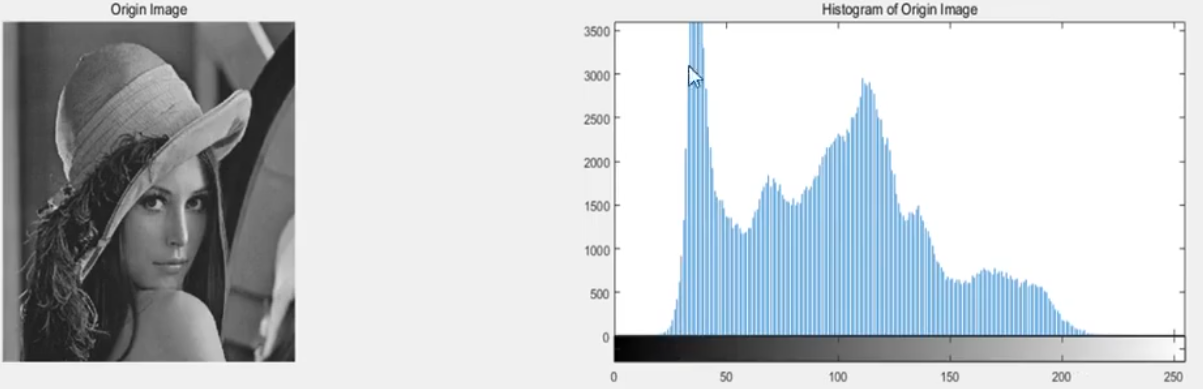
一、图像直方图统计原理

直方图的全称为灰度直方图，是对图像每一灰度间隔内像素个数的统计。即对一张图片中每隔二灰度值的像素数量做统计，然后以直方图的形式展现出来。图下的亮暗分布在直方图中就可以一目了然，直方图在图像前端和后端处理中都有广泛的应用，比如图像的直方图均衡、图像自动曝光控制和图像特征提取等。

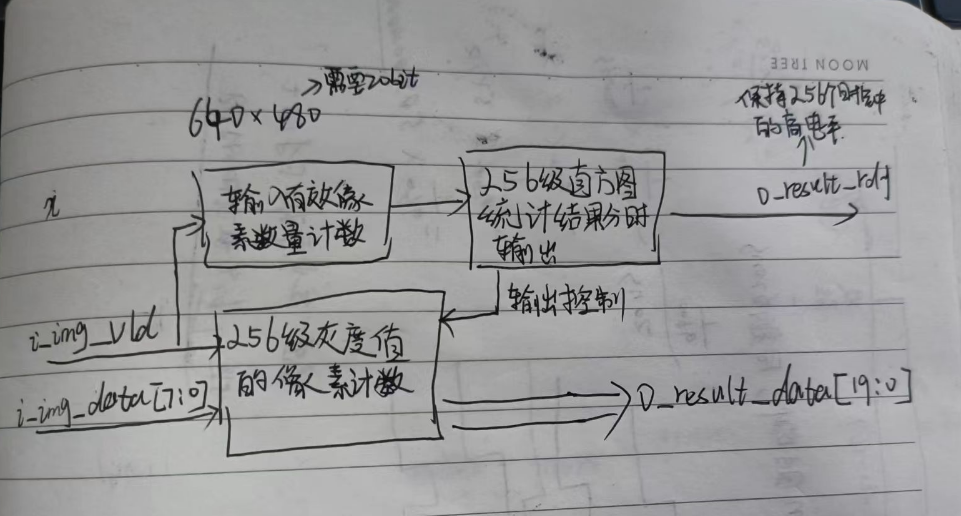
二、基于寄存器（逻辑资源）的直方图统计系统框图

图片大小640x480，需要20bit的位宽来计像素的个数。i_img_vld为高时，输入图片数据i_img_data[7:0]有效，“256级灰度灰度值的像素计数”模块统计0~255中灰度级数的个数，“输入有效像素个数计数”模块用于计算i_mg_data已经输入了几个，“256级直方图统计结果分时输出”模块是输入256个灰度级的统计结果，需要256个时钟周期，每个周期输出一级灰度级的结果。

三、代码实现

这个代码简单而且暴力，主要是易于理解，占用较多的逻辑资源。因为这种统计方法，对于i_image_data来说有256个扇出，所以系统时钟频率不会跑的很高，时序很难收敛

`timescale 1ns/1ps

module m_histogram_reg#(
	parameter P_IMAGE_WIDTH=640,
	parameter P_IMAGE_HIGHT=480

)(
	input i_clk,
	input i_rst_n,
	input i_image_vld,
	input [7:0] i_image_data,
	output reg o_result_rdy,
	output reg [19:0] o_result_data
    );
	
localparam P_IMAGE_SIZE = P_IMAGE_HIGHT*P_IMAGE_WIDTH;
reg [19:0] r_hist_cnt[255:0];//每个灰度值统计的计数器

//256个灰度值的直方图统计
always@(posedge i_clk)begin
	if(!i_rst_n)begin
		r_hist_cnt[0] <= 20'd0;
		r_hist_cnt[1] <= 20'd0;
		r_hist_cnt[2] <= 20'd0;
		r_hist_cnt[3] <= 20'd0;
		r_hist_cnt[4] <= 20'd0;
		r_hist_cnt[5] <= 20'd0;
		r_hist_cnt[6] <= 20'd0;
		r_hist_cnt[7] <= 20'd0;
		r_hist_cnt[8] <= 20'd0;
		r_hist_cnt[9] <= 20'd0;
		r_hist_cnt[10] <= 20'd0;
		r_hist_cnt[11] <= 20'd0;
		r_hist_cnt[12] <= 20'd0;
		r_hist_cnt[13] <= 20'd0;
		r_hist_cnt[14] <= 20'd0;
		r_hist_cnt[15] <= 20'd0;
		r_hist_cnt[16] <= 20'd0;
		r_hist_cnt[17] <= 20'd0;
		r_hist_cnt[18] <= 20'd0;
		r_hist_cnt[19] <= 20'd0;
		r_hist_cnt[20] <= 20'd0;
		r_hist_cnt[21] <= 20'd0;
		r_hist_cnt[22] <= 20'd0;
		r_hist_cnt[23] <= 20'd0;
		r_hist_cnt[24] <= 20'd0;
		r_hist_cnt[25] <= 20'd0;
		r_hist_cnt[26] <= 20'd0;
		r_hist_cnt[27] <= 20'd0;
		r_hist_cnt[28] <= 20'd0;
		r_hist_cnt[29] <= 20'd0;
		r_hist_cnt[30] <= 20'd0;
		r_hist_cnt[31] <= 20'd0;
		r_hist_cnt[32] <= 20'd0;
		r_hist_cnt[33] <= 20'd0;
		r_hist_cnt[34] <= 20'd0;
		r_hist_cnt[35] <= 20'd0;
		r_hist_cnt[36] <= 20'd0;
		r_hist_cnt[37] <= 20'd0;
		r_hist_cnt[38] <= 20'd0;
		r_hist_cnt[39] <= 20'd0;
		r_hist_cnt[40] <= 20'd0;
		r_hist_cnt[41] <= 20'd0;
		r_hist_cnt[42] <= 20'd0;
		r_hist_cnt[43] <= 20'd0;
		r_hist_cnt[44] <= 20'd0;
		r_hist_cnt[45] <= 20'd0;
		r_hist_cnt[46] <= 20'd0;
		r_hist_cnt[47] <= 20'd0;
		r_hist_cnt[48] <= 20'd0;
		r_hist_cnt[49] <= 20'd0;
		r_hist_cnt[50] <= 20'd0;
		r_hist_cnt[51] <= 20'd0;
		r_hist_cnt[52] <= 20'd0;
		r_hist_cnt[53] <= 20'd0;
		r_hist_cnt[54] <= 20'd0;
		r_hist_cnt[55] <= 20'd0;
		r_hist_cnt[56] <= 20'd0;
		r_hist_cnt[57] <= 20'd0;
		r_hist_cnt[58] <= 20'd0;
		r_hist_cnt[59] <= 20'd0;
		r_hist_cnt[60] <= 20'd0;
		r_hist_cnt[61] <= 20'd0;
		r_hist_cnt[62] <= 20'd0;
		r_hist_cnt[63] <= 20'd0;
		r_hist_cnt[64] <= 20'd0;
		r_hist_cnt[65] <= 20'd0;
		r_hist_cnt[66] <= 20'd0;
		r_hist_cnt[67] <= 20'd0;
		r_hist_cnt[68] <= 20'd0;
		r_hist_cnt[69] <= 20'd0;
		r_hist_cnt[70] <= 20'd0;
		r_hist_cnt[71] <= 20'd0;
		r_hist_cnt[72] <= 20'd0;
		r_hist_cnt[73] <= 20'd0;
		r_hist_cnt[74] <= 20'd0;
		r_hist_cnt[75] <= 20'd0;
		r_hist_cnt[76] <= 20'd0;
		r_hist_cnt[77] <= 20'd0;
		r_hist_cnt[78] <= 20'd0;
		r_hist_cnt[79] <= 20'd0;
		r_hist_cnt[80] <= 20'd0;
		r_hist_cnt[81] <= 20'd0;
		r_hist_cnt[82] <= 20'd0;
		r_hist_cnt[83] <= 20'd0;
		r_hist_cnt[84] <= 20'd0;
		r_hist_cnt[85] <= 20'd0;
		r_hist_cnt[86] <= 20'd0;
		r_hist_cnt[87] <= 20'd0;
		r_hist_cnt[88] <= 20'd0;
		r_hist_cnt[89] <= 20'd0;
		r_hist_cnt[90] <= 20'd0;
		r_hist_cnt[91] <= 20'd0;
		r_hist_cnt[92] <= 20'd0;
		r_hist_cnt[93] <= 20'd0;
		r_hist_cnt[94] <= 20'd0;
		r_hist_cnt[95] <= 20'd0;
		r_hist_cnt[96] <= 20'd0;
		r_hist_cnt[97] <= 20'd0;
		r_hist_cnt[98] <= 20'd0;
		r_hist_cnt[99] <= 20'd0;
		r_hist_cnt[100] <= 20'd0;
		r_hist_cnt[101] <= 20'd0;
		r_hist_cnt[102] <= 20'd0;
		r_hist_cnt[103] <= 20'd0;
		r_hist_cnt[104] <= 20'd0;
		r_hist_cnt[105] <= 20'd0;
		r_hist_cnt[106] <= 20'd0;
		r_hist_cnt[107] <= 20'd0;
		r_hist_cnt[108] <= 20'd0;
		r_hist_cnt[109] <= 20'd0;
		r_hist_cnt[110] <= 20'd0;
		r_hist_cnt[111] <= 20'd0;
		r_hist_cnt[112] <= 20'd0;
		r_hist_cnt[113] <= 20'd0;
		r_hist_cnt[114] <= 20'd0;
		r_hist_cnt[115] <= 20'd0;
		r_hist_cnt[116] <= 20'd0;
		r_hist_cnt[117] <= 20'd0;
		r_hist_cnt[118] <= 20'd0;
		r_hist_cnt[119] <= 20'd0;
		r_hist_cnt[120] <= 20'd0;
		r_hist_cnt[121] <= 20'd0;
		r_hist_cnt[122] <= 20'd0;
		r_hist_cnt[123] <= 20'd0;
		r_hist_cnt[124] <= 20'd0;
		r_hist_cnt[125] <= 20'd0;
		r_hist_cnt[126] <= 20'd0;
		r_hist_cnt[127] <= 20'd0;
		r_hist_cnt[128] <= 20'd0;
		r_hist_cnt[129] <= 20'd0;
		r_hist_cnt[130] <= 20'd0;
		r_hist_cnt[131] <= 20'd0;
		r_hist_cnt[132] <= 20'd0;
		r_hist_cnt[133] <= 20'd0;
		r_hist_cnt[134] <= 20'd0;
		r_hist_cnt[135] <= 20'd0;
		r_hist_cnt[136] <= 20'd0;
		r_hist_cnt[137] <= 20'd0;
		r_hist_cnt[138] <= 20'd0;
		r_hist_cnt[139] <= 20'd0;
		r_hist_cnt[140] <= 20'd0;
		r_hist_cnt[141] <= 20'd0;
		r_hist_cnt[142] <= 20'd0;
		r_hist_cnt[143] <= 20'd0;
		r_hist_cnt[144] <= 20'd0;
		r_hist_cnt[145] <= 20'd0;
		r_hist_cnt[146] <= 20'd0;
		r_hist_cnt[147] <= 20'd0;
		r_hist_cnt[148] <= 20'd0;
		r_hist_cnt[149] <= 20'd0;
		r_hist_cnt[150] <= 20'd0;
		r_hist_cnt[151] <= 20'd0;
		r_hist_cnt[152] <= 20'd0;
		r_hist_cnt[153] <= 20'd0;
		r_hist_cnt[154] <= 20'd0;
		r_hist_cnt[155] <= 20'd0;
		r_hist_cnt[156] <= 20'd0;
		r_hist_cnt[157] <= 20'd0;
		r_hist_cnt[158] <= 20'd0;
		r_hist_cnt[159] <= 20'd0;
		r_hist_cnt[160] <= 20'd0;
		r_hist_cnt[161] <= 20'd0;
		r_hist_cnt[162] <= 20'd0;
		r_hist_cnt[163] <= 20'd0;
		r_hist_cnt[164] <= 20'd0;
		r_hist_cnt[165] <= 20'd0;
		r_hist_cnt[166] <= 20'd0;
		r_hist_cnt[167] <= 20'd0;
		r_hist_cnt[168] <= 20'd0;
		r_hist_cnt[169] <= 20'd0;
		r_hist_cnt[170] <= 20'd0;
		r_hist_cnt[171] <= 20'd0;
		r_hist_cnt[172] <= 20'd0;
		r_hist_cnt[173] <= 20'd0;
		r_hist_cnt[174] <= 20'd0;
		r_hist_cnt[175] <= 20'd0;
		r_hist_cnt[176] <= 20'd0;
		r_hist_cnt[177] <= 20'd0;
		r_hist_cnt[178] <= 20'd0;
		r_hist_cnt[179] <= 20'd0;
		r_hist_cnt[180] <= 20'd0;
		r_hist_cnt[181] <= 20'd0;
		r_hist_cnt[182] <= 20'd0;
		r_hist_cnt[183] <= 20'd0;
		r_hist_cnt[184] <= 20'd0;
		r_hist_cnt[185] <= 20'd0;
		r_hist_cnt[186] <= 20'd0;
		r_hist_cnt[187] <= 20'd0;
		r_hist_cnt[188] <= 20'd0;
		r_hist_cnt[189] <= 20'd0;
		r_hist_cnt[190] <= 20'd0;
		r_hist_cnt[191] <= 20'd0;
		r_hist_cnt[192] <= 20'd0;
		r_hist_cnt[193] <= 20'd0;
		r_hist_cnt[194] <= 20'd0;
		r_hist_cnt[195] <= 20'd0;
		r_hist_cnt[196] <= 20'd0;
		r_hist_cnt[197] <= 20'd0;
		r_hist_cnt[198] <= 20'd0;
		r_hist_cnt[199] <= 20'd0;
		r_hist_cnt[200] <= 20'd0;
		r_hist_cnt[201] <= 20'd0;
		r_hist_cnt[202] <= 20'd0;
		r_hist_cnt[203] <= 20'd0;
		r_hist_cnt[204] <= 20'd0;
		r_hist_cnt[205] <= 20'd0;
		r_hist_cnt[206] <= 20'd0;
		r_hist_cnt[207] <= 20'd0;
		r_hist_cnt[208] <= 20'd0;
		r_hist_cnt[209] <= 20'd0;
		r_hist_cnt[210] <= 20'd0;
		r_hist_cnt[211] <= 20'd0;
		r_hist_cnt[212] <= 20'd0;
		r_hist_cnt[213] <= 20'd0;
		r_hist_cnt[214] <= 20'd0;
		r_hist_cnt[215] <= 20'd0;
		r_hist_cnt[216] <= 20'd0;
		r_hist_cnt[217] <= 20'd0;
		r_hist_cnt[218] <= 20'd0;
		r_hist_cnt[219] <= 20'd0;
		r_hist_cnt[220] <= 20'd0;
		r_hist_cnt[221] <= 20'd0;
		r_hist_cnt[222] <= 20'd0;
		r_hist_cnt[223] <= 20'd0;
		r_hist_cnt[224] <= 20'd0;
		r_hist_cnt[225] <= 20'd0;
		r_hist_cnt[226] <= 20'd0;
		r_hist_cnt[227] <= 20'd0;
		r_hist_cnt[228] <= 20'd0;
		r_hist_cnt[229] <= 20'd0;
		r_hist_cnt[230] <= 20'd0;
		r_hist_cnt[231] <= 20'd0;
		r_hist_cnt[232] <= 20'd0;
		r_hist_cnt[233] <= 20'd0;
		r_hist_cnt[234] <= 20'd0;
		r_hist_cnt[235] <= 20'd0;
		r_hist_cnt[236] <= 20'd0;
		r_hist_cnt[237] <= 20'd0;
		r_hist_cnt[238] <= 20'd0;
		r_hist_cnt[239] <= 20'd0;
		r_hist_cnt[240] <= 20'd0;
		r_hist_cnt[241] <= 20'd0;
		r_hist_cnt[242] <= 20'd0;
		r_hist_cnt[243] <= 20'd0;
		r_hist_cnt[244] <= 20'd0;
		r_hist_cnt[245] <= 20'd0;
		r_hist_cnt[246] <= 20'd0;
		r_hist_cnt[247] <= 20'd0;
		r_hist_cnt[248] <= 20'd0;
		r_hist_cnt[249] <= 20'd0;
		r_hist_cnt[250] <= 20'd0;
		r_hist_cnt[251] <= 20'd0;
		r_hist_cnt[252] <= 20'd0;
		r_hist_cnt[253] <= 20'd0;
		r_hist_cnt[254] <= 20'd0;
		r_hist_cnt[255] <= 20'd0;
	end 
	else if(i_image_vld)begin
		case(i_image_data)
			8'd0:r_hist_cnt[0] <=r_hist_cnt[0] + 1;
			8'd1:r_hist_cnt[1] <=r_hist_cnt[1] + 1;
			8'd2:r_hist_cnt[2] <=r_hist_cnt[2] + 1;
			8'd3:r_hist_cnt[3] <=r_hist_cnt[3] + 1;
			8'd4:r_hist_cnt[4] <=r_hist_cnt[4] + 1;
			8'd5:r_hist_cnt[5] <=r_hist_cnt[5] + 1;
			8'd6:r_hist_cnt[6] <=r_hist_cnt[6] + 1;
			8'd7:r_hist_cnt[7] <=r_hist_cnt[7] + 1;
			8'd8:r_hist_cnt[8] <=r_hist_cnt[8] + 1;
			8'd9:r_hist_cnt[9] <=r_hist_cnt[9] + 1;
			8'd10:r_hist_cnt[10] <=r_hist_cnt[10] + 1;
			8'd11:r_hist_cnt[11] <=r_hist_cnt[11] + 1;
			8'd12:r_hist_cnt[12] <=r_hist_cnt[12] + 1;
			8'd13:r_hist_cnt[13] <=r_hist_cnt[13] + 1;
			8'd14:r_hist_cnt[14] <=r_hist_cnt[14] + 1;
			8'd15:r_hist_cnt[15] <=r_hist_cnt[15] + 1;
			8'd16:r_hist_cnt[16] <=r_hist_cnt[16] + 1;
			8'd17:r_hist_cnt[17] <=r_hist_cnt[17] + 1;
			8'd18:r_hist_cnt[18] <=r_hist_cnt[18] + 1;
			8'd19:r_hist_cnt[19] <=r_hist_cnt[19] + 1;
			8'd20:r_hist_cnt[20] <=r_hist_cnt[20] + 1;
			8'd21:r_hist_cnt[21] <=r_hist_cnt[21] + 1;
			8'd22:r_hist_cnt[22] <=r_hist_cnt[22] + 1;
			8'd23:r_hist_cnt[23] <=r_hist_cnt[23] + 1;
			8'd24:r_hist_cnt[24] <=r_hist_cnt[24] + 1;
			8'd25:r_hist_cnt[25] <=r_hist_cnt[25] + 1;
			8'd26:r_hist_cnt[26] <=r_hist_cnt[26] + 1;
			8'd27:r_hist_cnt[27] <=r_hist_cnt[27] + 1;
			8'd28:r_hist_cnt[28] <=r_hist_cnt[28] + 1;
			8'd29:r_hist_cnt[29] <=r_hist_cnt[29] + 1;
			8'd30:r_hist_cnt[30] <=r_hist_cnt[30] + 1;
			8'd31:r_hist_cnt[31] <=r_hist_cnt[31] + 1;
			8'd32:r_hist_cnt[32] <=r_hist_cnt[32] + 1;
			8'd33:r_hist_cnt[33] <=r_hist_cnt[33] + 1;
			8'd34:r_hist_cnt[34] <=r_hist_cnt[34] + 1;
			8'd35:r_hist_cnt[35] <=r_hist_cnt[35] + 1;
			8'd36:r_hist_cnt[36] <=r_hist_cnt[36] + 1;
			8'd37:r_hist_cnt[37] <=r_hist_cnt[37] + 1;
			8'd38:r_hist_cnt[38] <=r_hist_cnt[38] + 1;
			8'd39:r_hist_cnt[39] <=r_hist_cnt[39] + 1;
			8'd40:r_hist_cnt[40] <=r_hist_cnt[40] + 1;
			8'd41:r_hist_cnt[41] <=r_hist_cnt[41] + 1;
			8'd42:r_hist_cnt[42] <=r_hist_cnt[42] + 1;
			8'd43:r_hist_cnt[43] <=r_hist_cnt[43] + 1;
			8'd44:r_hist_cnt[44] <=r_hist_cnt[44] + 1;
			8'd45:r_hist_cnt[45] <=r_hist_cnt[45] + 1;
			8'd46:r_hist_cnt[46] <=r_hist_cnt[46] + 1;
			8'd47:r_hist_cnt[47] <=r_hist_cnt[47] + 1;
			8'd48:r_hist_cnt[48] <=r_hist_cnt[48] + 1;
			8'd49:r_hist_cnt[49] <=r_hist_cnt[49] + 1;
			8'd50:r_hist_cnt[50] <=r_hist_cnt[50] + 1;
			8'd51:r_hist_cnt[51] <=r_hist_cnt[51] + 1;
			8'd52:r_hist_cnt[52] <=r_hist_cnt[52] + 1;
			8'd53:r_hist_cnt[53] <=r_hist_cnt[53] + 1;
			8'd54:r_hist_cnt[54] <=r_hist_cnt[54] + 1;
			8'd55:r_hist_cnt[55] <=r_hist_cnt[55] + 1;
			8'd56:r_hist_cnt[56] <=r_hist_cnt[56] + 1;
			8'd57:r_hist_cnt[57] <=r_hist_cnt[57] + 1;
			8'd58:r_hist_cnt[58] <=r_hist_cnt[58] + 1;
			8'd59:r_hist_cnt[59] <=r_hist_cnt[59] + 1;
			8'd60:r_hist_cnt[60] <=r_hist_cnt[60] + 1;
			8'd61:r_hist_cnt[61] <=r_hist_cnt[61] + 1;
			8'd62:r_hist_cnt[62] <=r_hist_cnt[62] + 1;
			8'd63:r_hist_cnt[63] <=r_hist_cnt[63] + 1;
			8'd64:r_hist_cnt[64] <=r_hist_cnt[64] + 1;
			8'd65:r_hist_cnt[65] <=r_hist_cnt[65] + 1;
			8'd66:r_hist_cnt[66] <=r_hist_cnt[66] + 1;
			8'd67:r_hist_cnt[67] <=r_hist_cnt[67] + 1;
			8'd68:r_hist_cnt[68] <=r_hist_cnt[68] + 1;
			8'd69:r_hist_cnt[69] <=r_hist_cnt[69] + 1;
			8'd70:r_hist_cnt[70] <=r_hist_cnt[70] + 1;
			8'd71:r_hist_cnt[71] <=r_hist_cnt[71] + 1;
			8'd72:r_hist_cnt[72] <=r_hist_cnt[72] + 1;
			8'd73:r_hist_cnt[73] <=r_hist_cnt[73] + 1;
			8'd74:r_hist_cnt[74] <=r_hist_cnt[74] + 1;
			8'd75:r_hist_cnt[75] <=r_hist_cnt[75] + 1;
			8'd76:r_hist_cnt[76] <=r_hist_cnt[76] + 1;
			8'd77:r_hist_cnt[77] <=r_hist_cnt[77] + 1;
			8'd78:r_hist_cnt[78] <=r_hist_cnt[78] + 1;
			8'd79:r_hist_cnt[79] <=r_hist_cnt[79] + 1;
			8'd80:r_hist_cnt[80] <=r_hist_cnt[80] + 1;
			8'd81:r_hist_cnt[81] <=r_hist_cnt[81] + 1;
			8'd82:r_hist_cnt[82] <=r_hist_cnt[82] + 1;
			8'd83:r_hist_cnt[83] <=r_hist_cnt[83] + 1;
			8'd84:r_hist_cnt[84] <=r_hist_cnt[84] + 1;
			8'd85:r_hist_cnt[85] <=r_hist_cnt[85] + 1;
			8'd86:r_hist_cnt[86] <=r_hist_cnt[86] + 1;
			8'd87:r_hist_cnt[87] <=r_hist_cnt[87] + 1;
			8'd88:r_hist_cnt[88] <=r_hist_cnt[88] + 1;
			8'd89:r_hist_cnt[89] <=r_hist_cnt[89] + 1;
			8'd90:r_hist_cnt[90] <=r_hist_cnt[90] + 1;
			8'd91:r_hist_cnt[91] <=r_hist_cnt[91] + 1;
			8'd92:r_hist_cnt[92] <=r_hist_cnt[92] + 1;
			8'd93:r_hist_cnt[93] <=r_hist_cnt[93] + 1;
			8'd94:r_hist_cnt[94] <=r_hist_cnt[94] + 1;
			8'd95:r_hist_cnt[95] <=r_hist_cnt[95] + 1;
			8'd96:r_hist_cnt[96] <=r_hist_cnt[96] + 1;
			8'd97:r_hist_cnt[97] <=r_hist_cnt[97] + 1;
			8'd98:r_hist_cnt[98] <=r_hist_cnt[98] + 1;
			8'd99:r_hist_cnt[99] <=r_hist_cnt[99] + 1;
			8'd100:r_hist_cnt[100] <=r_hist_cnt[100] + 1;
			8'd101:r_hist_cnt[101] <=r_hist_cnt[101] + 1;
			8'd102:r_hist_cnt[102] <=r_hist_cnt[102] + 1;
			8'd103:r_hist_cnt[103] <=r_hist_cnt[103] + 1;
			8'd104:r_hist_cnt[104] <=r_hist_cnt[104] + 1;
			8'd105:r_hist_cnt[105] <=r_hist_cnt[105] + 1;
			8'd106:r_hist_cnt[106] <=r_hist_cnt[106] + 1;
			8'd107:r_hist_cnt[107] <=r_hist_cnt[107] + 1;
			8'd108:r_hist_cnt[108] <=r_hist_cnt[108] + 1;
			8'd109:r_hist_cnt[109] <=r_hist_cnt[109] + 1;
			8'd110:r_hist_cnt[110] <=r_hist_cnt[110] + 1;
			8'd111:r_hist_cnt[111] <=r_hist_cnt[111] + 1;
			8'd112:r_hist_cnt[112] <=r_hist_cnt[112] + 1;
			8'd113:r_hist_cnt[113] <=r_hist_cnt[113] + 1;
			8'd114:r_hist_cnt[114] <=r_hist_cnt[114] + 1;
			8'd115:r_hist_cnt[115] <=r_hist_cnt[115] + 1;
			8'd116:r_hist_cnt[116] <=r_hist_cnt[116] + 1;
			8'd117:r_hist_cnt[117] <=r_hist_cnt[117] + 1;
			8'd118:r_hist_cnt[118] <=r_hist_cnt[118] + 1;
			8'd119:r_hist_cnt[119] <=r_hist_cnt[119] + 1;
			8'd120:r_hist_cnt[120] <=r_hist_cnt[120] + 1;
			8'd121:r_hist_cnt[121] <=r_hist_cnt[121] + 1;
			8'd122:r_hist_cnt[122] <=r_hist_cnt[122] + 1;
			8'd123:r_hist_cnt[123] <=r_hist_cnt[123] + 1;
			8'd124:r_hist_cnt[124] <=r_hist_cnt[124] + 1;
			8'd125:r_hist_cnt[125] <=r_hist_cnt[125] + 1;
			8'd126:r_hist_cnt[126] <=r_hist_cnt[126] + 1;
			8'd127:r_hist_cnt[127] <=r_hist_cnt[127] + 1;
			8'd128:r_hist_cnt[128] <=r_hist_cnt[128] + 1;
			8'd129:r_hist_cnt[129] <=r_hist_cnt[129] + 1;
			8'd130:r_hist_cnt[130] <=r_hist_cnt[130] + 1;
			8'd131:r_hist_cnt[131] <=r_hist_cnt[131] + 1;
			8'd132:r_hist_cnt[132] <=r_hist_cnt[132] + 1;
			8'd133:r_hist_cnt[133] <=r_hist_cnt[133] + 1;
			8'd134:r_hist_cnt[134] <=r_hist_cnt[134] + 1;
			8'd135:r_hist_cnt[135] <=r_hist_cnt[135] + 1;
			8'd136:r_hist_cnt[136] <=r_hist_cnt[136] + 1;
			8'd137:r_hist_cnt[137] <=r_hist_cnt[137] + 1;
			8'd138:r_hist_cnt[138] <=r_hist_cnt[138] + 1;
			8'd139:r_hist_cnt[139] <=r_hist_cnt[139] + 1;
			8'd140:r_hist_cnt[140] <=r_hist_cnt[140] + 1;
			8'd141:r_hist_cnt[141] <=r_hist_cnt[141] + 1;
			8'd142:r_hist_cnt[142] <=r_hist_cnt[142] + 1;
			8'd143:r_hist_cnt[143] <=r_hist_cnt[143] + 1;
			8'd144:r_hist_cnt[144] <=r_hist_cnt[144] + 1;
			8'd145:r_hist_cnt[145] <=r_hist_cnt[145] + 1;
			8'd146:r_hist_cnt[146] <=r_hist_cnt[146] + 1;
			8'd147:r_hist_cnt[147] <=r_hist_cnt[147] + 1;
			8'd148:r_hist_cnt[148] <=r_hist_cnt[148] + 1;
			8'd149:r_hist_cnt[149] <=r_hist_cnt[149] + 1;
			8'd150:r_hist_cnt[150] <=r_hist_cnt[150] + 1;
			8'd151:r_hist_cnt[151] <=r_hist_cnt[151] + 1;
			8'd152:r_hist_cnt[152] <=r_hist_cnt[152] + 1;
			8'd153:r_hist_cnt[153] <=r_hist_cnt[153] + 1;
			8'd154:r_hist_cnt[154] <=r_hist_cnt[154] + 1;
			8'd155:r_hist_cnt[155] <=r_hist_cnt[155] + 1;
			8'd156:r_hist_cnt[156] <=r_hist_cnt[156] + 1;
			8'd157:r_hist_cnt[157] <=r_hist_cnt[157] + 1;
			8'd158:r_hist_cnt[158] <=r_hist_cnt[158] + 1;
			8'd159:r_hist_cnt[159] <=r_hist_cnt[159] + 1;
			8'd160:r_hist_cnt[160] <=r_hist_cnt[160] + 1;
			8'd161:r_hist_cnt[161] <=r_hist_cnt[161] + 1;
			8'd162:r_hist_cnt[162] <=r_hist_cnt[162] + 1;
			8'd163:r_hist_cnt[163] <=r_hist_cnt[163] + 1;
			8'd164:r_hist_cnt[164] <=r_hist_cnt[164] + 1;
			8'd165:r_hist_cnt[165] <=r_hist_cnt[165] + 1;
			8'd166:r_hist_cnt[166] <=r_hist_cnt[166] + 1;
			8'd167:r_hist_cnt[167] <=r_hist_cnt[167] + 1;
			8'd168:r_hist_cnt[168] <=r_hist_cnt[168] + 1;
			8'd169:r_hist_cnt[169] <=r_hist_cnt[169] + 1;
			8'd170:r_hist_cnt[170] <=r_hist_cnt[170] + 1;
			8'd171:r_hist_cnt[171] <=r_hist_cnt[171] + 1;
			8'd172:r_hist_cnt[172] <=r_hist_cnt[172] + 1;
			8'd173:r_hist_cnt[173] <=r_hist_cnt[173] + 1;
			8'd174:r_hist_cnt[174] <=r_hist_cnt[174] + 1;
			8'd175:r_hist_cnt[175] <=r_hist_cnt[175] + 1;
			8'd176:r_hist_cnt[176] <=r_hist_cnt[176] + 1;
			8'd177:r_hist_cnt[177] <=r_hist_cnt[177] + 1;
			8'd178:r_hist_cnt[178] <=r_hist_cnt[178] + 1;
			8'd179:r_hist_cnt[179] <=r_hist_cnt[179] + 1;
			8'd180:r_hist_cnt[180] <=r_hist_cnt[180] + 1;
			8'd181:r_hist_cnt[181] <=r_hist_cnt[181] + 1;
			8'd182:r_hist_cnt[182] <=r_hist_cnt[182] + 1;
			8'd183:r_hist_cnt[183] <=r_hist_cnt[183] + 1;
			8'd184:r_hist_cnt[184] <=r_hist_cnt[184] + 1;
			8'd185:r_hist_cnt[185] <=r_hist_cnt[185] + 1;
			8'd186:r_hist_cnt[186] <=r_hist_cnt[186] + 1;
			8'd187:r_hist_cnt[187] <=r_hist_cnt[187] + 1;
			8'd188:r_hist_cnt[188] <=r_hist_cnt[188] + 1;
			8'd189:r_hist_cnt[189] <=r_hist_cnt[189] + 1;
			8'd190:r_hist_cnt[190] <=r_hist_cnt[190] + 1;
			8'd191:r_hist_cnt[191] <=r_hist_cnt[191] + 1;
			8'd192:r_hist_cnt[192] <=r_hist_cnt[192] + 1;
			8'd193:r_hist_cnt[193] <=r_hist_cnt[193] + 1;
			8'd194:r_hist_cnt[194] <=r_hist_cnt[194] + 1;
			8'd195:r_hist_cnt[195] <=r_hist_cnt[195] + 1;
			8'd196:r_hist_cnt[196] <=r_hist_cnt[196] + 1;
			8'd197:r_hist_cnt[197] <=r_hist_cnt[197] + 1;
			8'd198:r_hist_cnt[198] <=r_hist_cnt[198] + 1;
			8'd199:r_hist_cnt[199] <=r_hist_cnt[199] + 1;
			8'd200:r_hist_cnt[200] <=r_hist_cnt[200] + 1;
			8'd201:r_hist_cnt[201] <=r_hist_cnt[201] + 1;
			8'd202:r_hist_cnt[202] <=r_hist_cnt[202] + 1;
			8'd203:r_hist_cnt[203] <=r_hist_cnt[203] + 1;
			8'd204:r_hist_cnt[204] <=r_hist_cnt[204] + 1;
			8'd205:r_hist_cnt[205] <=r_hist_cnt[205] + 1;
			8'd206:r_hist_cnt[206] <=r_hist_cnt[206] + 1;
			8'd207:r_hist_cnt[207] <=r_hist_cnt[207] + 1;
			8'd208:r_hist_cnt[208] <=r_hist_cnt[208] + 1;
			8'd209:r_hist_cnt[209] <=r_hist_cnt[209] + 1;
			8'd210:r_hist_cnt[210] <=r_hist_cnt[210] + 1;
			8'd211:r_hist_cnt[211] <=r_hist_cnt[211] + 1;
			8'd212:r_hist_cnt[212] <=r_hist_cnt[212] + 1;
			8'd213:r_hist_cnt[213] <=r_hist_cnt[213] + 1;
			8'd214:r_hist_cnt[214] <=r_hist_cnt[214] + 1;
			8'd215:r_hist_cnt[215] <=r_hist_cnt[215] + 1;
			8'd216:r_hist_cnt[216] <=r_hist_cnt[216] + 1;
			8'd217:r_hist_cnt[217] <=r_hist_cnt[217] + 1;
			8'd218:r_hist_cnt[218] <=r_hist_cnt[218] + 1;
			8'd219:r_hist_cnt[219] <=r_hist_cnt[219] + 1;
			8'd220:r_hist_cnt[220] <=r_hist_cnt[220] + 1;
			8'd221:r_hist_cnt[221] <=r_hist_cnt[221] + 1;
			8'd222:r_hist_cnt[222] <=r_hist_cnt[222] + 1;
			8'd223:r_hist_cnt[223] <=r_hist_cnt[223] + 1;
			8'd224:r_hist_cnt[224] <=r_hist_cnt[224] + 1;
			8'd225:r_hist_cnt[225] <=r_hist_cnt[225] + 1;
			8'd226:r_hist_cnt[226] <=r_hist_cnt[226] + 1;
			8'd227:r_hist_cnt[227] <=r_hist_cnt[227] + 1;
			8'd228:r_hist_cnt[228] <=r_hist_cnt[228] + 1;
			8'd229:r_hist_cnt[229] <=r_hist_cnt[229] + 1;
			8'd230:r_hist_cnt[230] <=r_hist_cnt[230] + 1;
			8'd231:r_hist_cnt[231] <=r_hist_cnt[231] + 1;
			8'd232:r_hist_cnt[232] <=r_hist_cnt[232] + 1;
			8'd233:r_hist_cnt[233] <=r_hist_cnt[233] + 1;
			8'd234:r_hist_cnt[234] <=r_hist_cnt[234] + 1;
			8'd235:r_hist_cnt[235] <=r_hist_cnt[235] + 1;
			8'd236:r_hist_cnt[236] <=r_hist_cnt[236] + 1;
			8'd237:r_hist_cnt[237] <=r_hist_cnt[237] + 1;
			8'd238:r_hist_cnt[238] <=r_hist_cnt[238] + 1;
			8'd239:r_hist_cnt[239] <=r_hist_cnt[239] + 1;
			8'd240:r_hist_cnt[240] <=r_hist_cnt[240] + 1;
			8'd241:r_hist_cnt[241] <=r_hist_cnt[241] + 1;
			8'd242:r_hist_cnt[242] <=r_hist_cnt[242] + 1;
			8'd243:r_hist_cnt[243] <=r_hist_cnt[243] + 1;
			8'd244:r_hist_cnt[244] <=r_hist_cnt[244] + 1;
			8'd245:r_hist_cnt[245] <=r_hist_cnt[245] + 1;
			8'd246:r_hist_cnt[246] <=r_hist_cnt[246] + 1;
			8'd247:r_hist_cnt[247] <=r_hist_cnt[247] + 1;
			8'd248:r_hist_cnt[248] <=r_hist_cnt[248] + 1;
			8'd249:r_hist_cnt[249] <=r_hist_cnt[249] + 1;
			8'd250:r_hist_cnt[250] <=r_hist_cnt[250] + 1;
			8'd251:r_hist_cnt[251] <=r_hist_cnt[251] + 1;
			8'd252:r_hist_cnt[252] <=r_hist_cnt[252] + 1;
			8'd253:r_hist_cnt[253] <=r_hist_cnt[253] + 1;
			8'd254:r_hist_cnt[254] <=r_hist_cnt[254] + 1;
			8'd255:r_hist_cnt[255] <=r_hist_cnt[255] + 1;
			default:;
		endcase
	end 
	
	else;
	
end 	

//输入像素计数器,一张图片已经输入了多少个像素
reg[19:0] r_pix_cnt;
wire w_one_frame_done;//一帧图像处理完成标志
always@(posedge i_clk) begin
	if(!i_rst_n)
		r_pix_cnt <= 20'd0;
	else if(w_one_frame_done)//计满一帧图像是，计数器清零。
		r_pix_cnt <=0;
	else if(i_image_vld)
		r_pix_cnt <= r_pix_cnt + 1;
	else;
end 

assign w_one_frame_done = (r_pix_cnt==P_IMAGE_SIZE)?1:0;

//直方图统计结果输出计数

reg [8:0] r_result_cnt;

always@(posedge i_clk) begin
	if(!i_rst_n)
		r_result_cnt<=9'd0;
	else if(w_one_frame_done)
		r_result_cnt <= 9'd1;
	else if( (r_result_cnt>9'd0) && (r_result_cnt<9'd256)) 
		r_result_cnt <= r_result_cnt +1;
	else
		r_result_cnt<=9'd0;
end 

//直方图统计结果的输出
//output reg o_result_rdy,
//output reg [19:0] o_result_data
always@(posedge i_clk) begin
	if(!i_rst_n)
		o_result_rdy <= 0;
	else if(r_result_cnt !=9'd0)
		o_result_rdy <= 1;
	else
		o_result_rdy <=0;
end 	

always@(posedge i_clk) begin
	o_result_data <= r_hist_cnt[r_result_cnt-1];
end 	

endmodule


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
479
480
481
482
483
484
485
486
487
488
489
490
491
492
493
494
495
496
497
498
499
500
501
502
503
504
505
506
507
508
509
510
511
512
513
514
515
516
517
518
519
520
521
522
523
524
525
526
527
528
529
530
531
532
533
534
535
536
537
538
539
540
541
542
543
544
545
546
547
548
549
550
551
552
553
554
555
556
557
558
559
560
561
562
563
564
565
566
567
568
569
570
571
572
573
574
575
576
577
578
579
580
581
582
583
584
585
586
587
588
589
590
591
592
593
594

直方图滤波的Matalb实现可以参考我另一篇博客，里面详细介绍了直方图滤波的原理：
MATLAB图像处理之【直方图均衡】传送门

--晓凡  2024年4月28日于武汉书
1