数据结构之哈希表（HASH）_数据表hash

前言

　　　当我们在编程过程中，往往需要对线性表进行查找操作。在顺序表中查找时，需要从表头开始，依次遍历比较a[i]与key的值是否相等，直到相等才返回索引i；在有序表中查找时，我们经常使用的是二分查找，通过比较key与a[i]的大小来折半查找，直到相等时才返回索引i。最终通过索引找到我们要找的元素。
　　　但是，这两种方法的效率都依赖于查找中比较的次数。我们有一种想法，能不能不经过比较，而是直接通过关键字key一次得到所要的结果呢？这时，就有了散列表查找（哈希表）。

1、什么是哈希表

　　　 要说哈希表，我们必须先了解一种新的存储方式—散列技术。
　　　 散列技术是指在记录的存储位置和它的关键字之间建立一个确定的对应关系f，使每一个关键字都对应一个存储位置。即：存储位置=f（关键字）。这样，在查找的过程中，只需要通过这个对应关系f 找到给定值key的映射f（key）。只要集合中存在关键字和key相等的记录，则必在存储位置f（key）处。我们把这种对应关系f 称为散列函数或哈希函数。
　　　 按照这个思想，采用散列技术将记录存储在一块连续的存储空间中，这块连续的存储空间称为哈希表。所得的存储地址称为哈希地址或散列地址。

2、哈希表查找步骤

　　　①、存储数据时，将数据存入通过哈希函数计算所得哪那个地址里面。
　　　②、查找时，使用同一个哈希函数通过关键字key计算出存储地址，通过该地址即可访问到查找的记录。

3、哈希冲突

　　在理想的情况下，每一个 关键字，通过哈希函数计算出来的地址都是不一样的。但是在实际情况中，我们常常会碰到两个关键字key1≠key2,但是f(key1) = f(key2), 这种现象称为冲突，并把key1和key2称为这个散列函数的同义词。
　　冲突的出现会造成查找上的错误，具体解决方法会在后文提到。

4、哈希函数的构造方法

（1）、原则

　　①、计算简单；
　　②、散列地址分布均匀。

（2）、构造方法

　　①、直接定址法：不常用
　　 　取关键字或关键字的某个线性函数值为哈希地址：
　　 　即：Ｈ(key) = key 或 H(key) = a*key+b
　　　　优点：简单，均匀，不会产生冲突；
　　　　缺点：需要实现直到关键字的分布情况，适合查找表比较小且连续的情况。
　　
　　②、数字分析法
　　　数字分析法用于处理关键字是位数比较多的数字，通过抽取关键字的一部分进行操作，计算哈希存储位置的方法。
　　　例如：关键字是手机号时，众所周知，我们的１１位手机号中，前三位是接入号，一般对应不同运营商的子品牌；中间四位是ＨＬＲ识别号，表示用户号的归属地；最后四位才是真正的用户号，所以我们可以选择后四位成为哈希地址，对其在进行相应操作来减少冲突。
　　　数字分析法适合处理关键字位数比较大的情况，事先知道关键字的分布且关键字的若干位分布均匀。
　　　
　　③、平方取中法
　　　具体方法很简单：先对关键字取平方，然后选取中间几位为哈希地址；取的位数由表长决定，适用于不知道关键字的分布，而位数又不是很大的情况。
　　
　　④、折叠法
　　 将关键字分成位数相同的几部分（最后一部分位数 可以不同），然后求这几部分的叠加和（舍去进位），并按照散列表的表长，取后几位作为哈希地址。
　　 适用于关键字位数很多，而且关键字每一位上数字分布大致均匀。
　　
　　 ⑤、除留余数法
　　 此方法为最常用的构造哈希函数方法。对于哈希表长为m的哈希函数公式为：
　　 f(key) = key mod p (p <= m)
　　 此方法不仅可以对关键字直接取模，也可以在折叠、平方取中之后再取模。
　　 所以，本方法的关键在于选择合适的p，若是p选择的不好，就可能产生 同义词；根据前人经验，若散列表的表长为m，通常p为小于或等于表长（最好接近m）的最小质数或不包含小于20质因子的合数。
　　
　　 ⑥、随机数法
　　 选择一个随机数，取关键字的随机函数值作为他的哈希地址。
　　 即：f(key) = random (key)
　　 当关键字的长度不等时，采用这个方法构造哈希函数较为合适。当遇到特殊字符的关键字时，需要将其转换为某种数字。

（3）、参考因素

　　　在实际应用过程中，应该视不同的情况采用不同的哈希函数。下列是一些参考因素：
　　　　①计算哈希地址所需的时间；
　　　　②关键字的长度；
　　　　③哈希表的大小；
　　　　④关键字的分布情况；
　　　　⑤查找的频率。
　　　选择哈希函数时，我们应该综合以上因素，选择合适的构建哈希函数的方法。

５、哈希冲突的解决

　　　前文提到，哈希冲突不能避免，所以我们需要找到方法来解决它。
　　　哈希冲突的解决方案主要有四种：开放地址法；再哈希；链地址法；公共溢出区法。

（1）、开放地址法　　

　　 开放地址法就是指：一旦发生了冲突就去寻找下一个空的哈希地址，只要哈希表足够大，空的散列地址总能找到，并将记录存入。
　　 公式：Hi=(H(*key) + Di) mod m (i = 1,2,3,….,k k<=m-1)
　　 其中：H（key）为哈希函数；m为哈希表表长；Di为增量序列，有以下3中取法:
　　 　　①Di = 1,2,3,…,m-1, 称为线性探测再散列；
　　 　　②Di = 1²，－１²，２²，－２²，。。。，±ｋ²，（ｋ<= m/2)称为二次探测再散列
　　 　　③Di = 伪随机数序列，称为伪随机数探测再散列。
　　 　　例如：在长度为12的哈希表中插入关键字为38的记录：
　　 　　
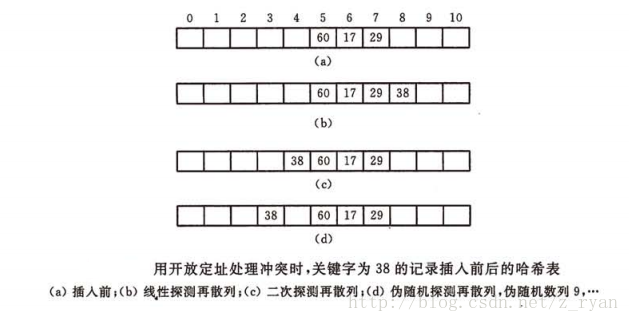
　　 　　从上述线性探测再散列的过程中可以看出一个现象：当表中i、i+1位置上有记录时，下一个哈希地址为i、i+1、i+2的记录都将填入i+3的位置，这种本不是同义词却要争夺同一个地址的现象叫“堆积“。即在处理同义词的冲突过程中又添加了非同义词的冲突；但是，用线探测再散列处理冲突可以保证：只要哈希表未填满，总能找到一个不发生冲突的地方。

（2）、再哈希法

　　 　　公式：Hi = RHi（key） i = 1，2，…，k
　　 　　RHi均是不同的哈希函数，意思为：当繁盛冲突时，使用不同的哈希函数计算地址，直到不冲突为止。这种方法不易产生堆积，但是耗费时间。

（3）、链地址法

　　 　　将所有关键字为同义字的记录存储在一个单链表中，我们称这种单链表为同义词子表，散列表中存储同义词子表的头指针。
　　 　　如关键字集合为{19，14，23，01，68，20，84，27，55，11，10，79}，按哈希函数H（key） = key mod 13；
　　 　　
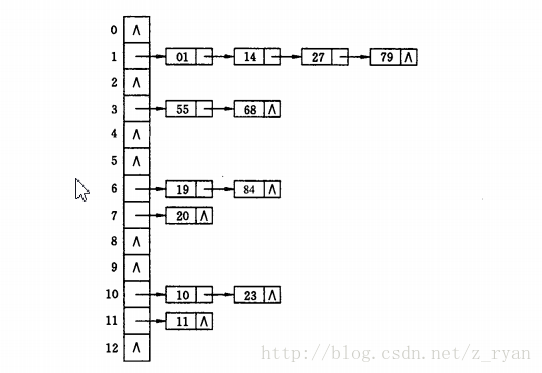
　　 　　链地址法解决了冲突，提供了永远都能找到地址的保证。但是，也带来了查找时需要遍历单链表的性能损耗。

（4）、公共溢出区法

　　 　　即设立两个表：基础表和溢出表。将所有关键字通过哈希函数计算出相应的地址。然后将未发生冲突的关键字放入相应的基础表中，一旦发生冲突，就将其依次放入溢出表中即可。
　　 　　在查找时，先用给定值通过哈希函数计算出相应的散列地址后，首先 首先与基本表的相应位置进行比较，如果不相等，再到溢出表中顺序查找。

6、哈希表查找算法的实现

　　　首先定义一个散列表的结构以及一些相关的常数。其中，HashTables是散列表结构。结构当中的elem为一个动态数组。

#define SUCCESS 1
#define UNSUCCESS 0
#define HASHSIZE 12    /*定义哈希表长为数组的长度*/
#define NULLKEY -32768
{
    int *elem;        /*数组元素存储基址，动态分配数组*/
    int count;        /*当前数据元素的个数*/
}HashTable;
int m = 0;            
1
2
3
4
5
6
7
8
9

初始化哈希表

/*初始化哈希表*/
Status InitHashTable(HashTable *H)
{
    int i;
    m = HASHSIZE;
    H->count = m;
    H->elem = (int *)malloc(m*sizeof(int));
    for(i = 0;i<m;i++)
        H->elem[i] = NULLKEY;

    return OK;
}   
1
2
3
4
5
6
7
8
9
10
11
12

定义哈希函数

/*哈希函数*/
int Hash(int key)
{
    return key % m;     /*除留取余法*/
}
1
2
3
4
5

插入操作

/*将关键字插入散列表*/
void InsertHash(HashTable *H,int key)
｛
     int addr = Hash(Key);             /*求哈希地址*/
     while(H->elem[addr] != NULLKEY)         /*如果不为空则冲突*/
         addr = (addr + 1) % m;           /*线性探测*/
     H->elem[addr] = key;            /*直到有空位后插入关键字*/        
｝   
1
2
3
4
5
6
7
8

查找操作

/*查找*/
Status SearchHash(HashTable H,int key,int *addr)
{
    *addr = Hash(key);        /*求哈希地址*/
    while(H.elem[*addr] != key)        /*若不为空，则冲突*/
    ｛
        *addr = (*addr + 1) % m;         /*线性探测*/
        if(H.elem[*addr) == NULLKEY || *addr == Hash(key))
        {/*如果循环回到原点*/
            return UNSUCCESS;        /*则说明关键字不存在*/
        }
    ｝
    return SUCCESS;
}   
1
2
3
4
5
6
7
8
9
10
11
12
13
14

7、总结

　　１、哈希表就是一种以键值对存储数据的结构。
　　2、哈希表是一个在空间和时间上做出权衡的经典例子。如果没有内存限制，那么可以
直接将键作为数组的索引。那么所查找的时间复杂度为Ｏ(1);如果没有时间限制，那么我们可以使用无序数组并进行顺序查找，这样只需要很少的内存。哈希表使用了适度的时间和空间来在这两个极端之间找到了平衡。只需要调整哈希函数算法即可在时间和空间上做出取舍。