中缀表达式转后缀表达式详解

(1)背景

 中缀表达式是最常用的算术表达式形式——运算符在运算数中间。但运算时需要考虑运算符优先级。

​  后缀表达式是计算机容易运算的表达式，运算符在运算数后面，从左到右进行运算,无需考虑优先级,运算呈线性结构。

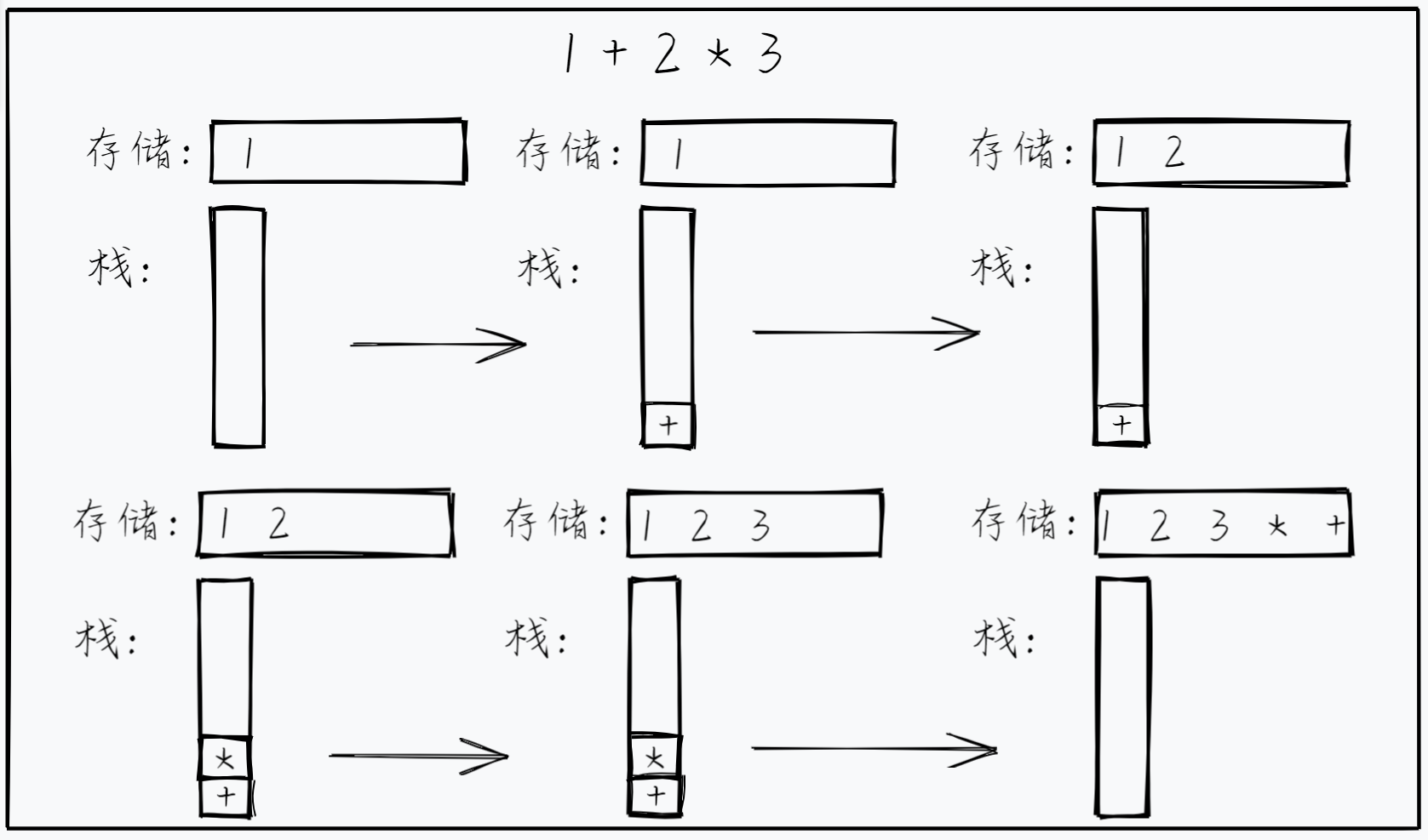
1 + 2 * 3// 中缀表达式
1 2 3 * +// 后缀表达式
1
2

​  计算机直接处理中缀表达式是比较困难的，以表达式1 + 2 * 3为例：当计算机读取到1 + 2后就可以直接得出结果3了吗？答案是否定的，因为后面可能会有优先级更高的运算符。

 ​ 就拿2来说，究竟是先和左操作数计算还是先与右操作数计算？这才是解决这类问题的核心与本质。

(2)中缀表达式转后缀表达式

1.最简单的情况：

后缀表达式也叫逆波兰表达式，我们可以通过以下的方法将中缀表达式转化为后缀表达式（我们用一个栈来临时存储中间遇到的操作符）：

1. 遇到 操作数，直接存储/输出

2. 遇到 操作符

   • 栈为空或者该操作符的优先级比栈顶的操作符的优先级高 → 将该操作符压栈
   • 该操作符的优先级比栈顶的操作符优先级低 or 相同 → 弹出栈顶操作符存储，并将该操作符压栈

3. 遍历结束后将栈里的操作符依次全部弹出，依次存储在末尾（或者直接输出）

2.原理分析：

​  我们以 n1 <O1> n2 <O2> n3 <O3> n4…… 为例加以说明，其中 n_i 表示操作数，O_i 表示操作符。

（1）如果 O1 的优先级高于 O2，那么毫无疑问，n2 会先与左操作数运算。

（2）如果 O1 的优先级低于 O2，那么可以让 n2 与右操作数 n3 发生运算吗？答案是否定的！因为n3 能不能先与 n2 运算还取决于 O2 O3 运算符优先级的高低。但是目前我们可以确定 O2 运算符肯定在 O1 运算符前被使用。

​  O1 操作符先进入，但是在情况二中因为优先级低，只能后运算。能够存储这种先进后出模式的数据结构，栈自然是不二之选！！

3.问题延伸：

1) 对于括号怎么处理?

​  从上面的学习中我们不难发现，先出栈的运算符一定比后出栈的运算符先运算。而括号作为优先级最高的运算符，我们如何体现出它的“优越性”呢?

​  其实处理的办法很简单，进入左括号后遇到的第一个运算符无脑压栈，不管优先级高低。这样就可以保证优先运算。

​  其实可以将括号里的式子看成一个个独立的式子，式子的结束就是遇到右括号的时候。在结束时，我们需要把这个独立子式中的操作符依次全部弹出（左括号之上的操作符，之下的可不归你管）

2) 对于负数怎么处理?

负数会在什么情况下出现呢? 我们不妨简化一下问题，对于一个标准的式子来说：

• 表达式的开始，例如 -1 + 5 * 3；
• 括号的开始，例如 3 + (-6) / 2;

我想到了两种思路来处理：

1. 如果 - 出现在式子的开头，我们则认为其代表负号而非减号
2. 我们只需在遇到负数时首先存储一个0，这样就可以通过减法来模拟负数

4.中缀转后缀参考代码：

这段代码中采用思路一，即需要根据 - 出现的位置判断究竟是减号还是负号。好处是我们便于得到中间的结果——后缀表达式，如果不需要这个结果只是想计算一个中缀表达式最后的结果，推荐参考文章最后一部分中缀表达式直接求解的部分，思路上更加清晰

#include <iostream>
#include <stack>
#include <vector>
#include <string>

#define cmp(c)  (c == '*' || c == '/')? (1) : (0)
using namespace std;

class calc {
public:
	// 中缀表达式转后缀
	void infix2Postfix(const string& s) {
		int n = s.size();
		char top_op;                      // 用来临时存放栈顶的元素
		for (int i = 0; i < n; ++i) {
			if (s[i] == ' ') continue;
			if (first && s[i] == '-') {   // 作为负号而非减号，不需要后续的压栈处理
				sign = -1;
				first = false;
				continue;
			}
			first = false;

			if (isdigit(s[i])) {        // 如果遇到数字，计算后直接存储
				int num = s[i] - '0';
				while (i + 1 < n && isdigit(s[i + 1])) {
					num = num * 10 + (s[++i] - '0');
				}
				output.push_back(to_string(num * sign));
				sign = 1;
			}
			else if (s[i] == '(') {      // 遇到左括号，遇到的下一个 op 可以无脑压栈
				first = true;
				priority = true;
				op.push('(');
			}
			else if (s[i] == ')') {
				priority = false;           // 避免 () 中没有运算符的情况，这样 priority 就带出到了括号外
				while (op.top() != '(') {   // 将 `()` 中的运算符出栈
					top_op = op.top();
					output.emplace_back(1, top_op);
					op.pop();
				}
				op.pop();                   // 最后弹出栈顶的失效的 '('
			}
			else {
				if (op.empty() || priority) { // ‘(’ 的最高优先级就是由 priority保证的 
					op.push(s[i]);
					priority = false;  
				}
				else {
					top_op = op.top();
					if (cmp(top_op) >= cmp(s[i])) {
						output.emplace_back(1, top_op);
						op.pop();
					}
					op.push(s[i]);
				}
			}
		}
		while (!op.empty()) {        // 将剩余的操作符依次全部弹出
			top_op = op.top();
			output.emplace_back(1, top_op);
			op.pop();
		}
		for (const auto& e : output) {
			cout << e << " ";
		}
		cout << endl;
	}
private:
	int sign = 1;             // 代表数字的正负号
	bool first = true;         // 如果 '-' 作为第一个字符出现，那么将其视为负号而非减号
	bool priority = false;     // 进入 ( 的第一个运算符具有压栈的最高优先级
	vector<string> output;     // 存储“输出”的结果
	stack<char> op;            // 用栈保存操作符
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77

(3)后缀表达式的最终求解

​  转化为后缀表达式后，我们就不需要考虑运算符优先级的高低，利用下面的方法就可以求出最终的结果：

• 遇到操作数 → 直接入栈

• 遇到操作符 → 取出栈顶的两个数据进行运算，将计算结果压栈

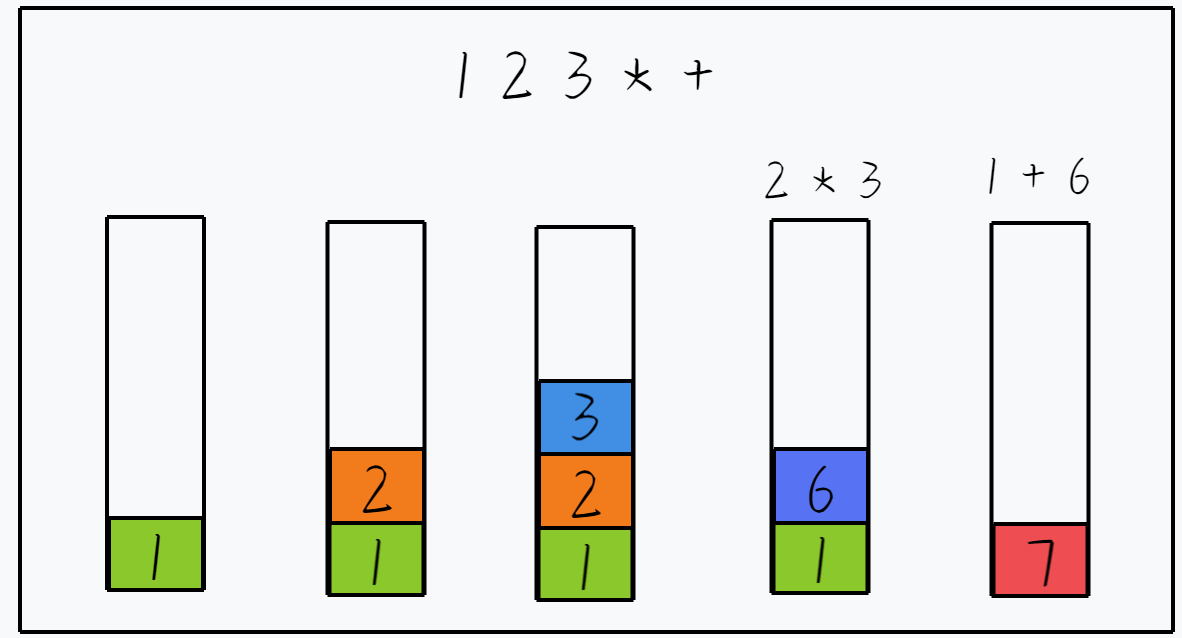
（注意：转换过程中操作数的相对位置始终没有发生改变，所以栈最顶上的是右操作数，它下面的才是左操作数）

class calc {
public:
	void infix2Postfix(const string& s) {
		// 略……
	}

  	int calcPostfix() {
		stack<int> res;
		for (const auto& token : output) {
			if (isNumber(token)) {
				res.push(atoi(token.c_str()));
			}
			else {
				int right = res.top();
				res.pop();
				int left = res.top();
				res.pop();
				switch (token[0]) {
				case '+':
					res.push(left + right);
					break;
				case '-':
					res.push(left - right);
					break;
				case '*':
					res.push(left * right);
					break;
				case '/':
					res.push(left / right);
					break;
				}
			}
		}
		return res.top();
	}
private:
	bool isNumber(const string& s) {
		return !(s == "+" || s == "-" || s == "*" || s == "/");
	}
private: 
	// 成员变量略……
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

(4)中缀表达式的直接求解

这里采用减法来模拟负数，从而避免了 - 是减号还是符号的苦恼，从而让代码在形式上更加统一，思路上也更加简单

inline int priority(char c) {
	return c == '*' || c == '/' ? (1) : (0);
}

class calc
{
public:
	// 例：s = “1 + 6 / 3”
	int eval(const string& s)
	{
		int sz = s.size();
		if (s[0] == '-') //[解释]：对负数的处理，通过减法来模拟负数
			num.push(0);

		for (int i = 0; i < sz; ++i)
		{
			if (s[i] == ' ')
				continue;
			else if (isdigit(s[i])) //[作用]：字符串转数字的操作
			{
				int n = s[i] - '0';
				while (i + 1 < sz && isdigit(s[i + 1]))
					n = n * 10 + (s[++i] - '0');
				num.push(n);
			}
			else if (s[i] == '(')
			{
				op.push('(');
				flag = true;//[解释]：标记进入左括号，下一个 op 无脑压栈 
				if (s[i + 1] == '-')
					num.push(0);
			}
			else if (s[i] == ')')
			{
				flag = false;
				// [注意]：在遇到左括号后的第一个运算符后，flag才会被重置为
				// false，但遇到括号里无运算符的情况就可能会出错，所以加个双保险
				char _operator = op.top();
				while (_operator != '(')
				{
					// [解释]：弹出运算符进行运算的过程
					count_push(_operator);
					op.pop();
					_operator = op.top();
				}
				op.pop();  // 把'('弹出来
			}
			else
			{
				if (op.empty() || flag)
				{
					op.push(s[i]);
					flag = false;
				}
				else
				{
					/**
					* 注意，这里必须采用 while 而非 if，因为同运算级的操作符必须从左往右
					* 使用 if 每次只是弹出一个操作符，这可能会导致同级运算符从右往左计算的出现
					* 例如 0-5*6+(-1) -> 0-30+(-1)， 如果 - 不立即与 30 运算，那们 + 就会
					* 压入栈顶，变成了 0-(30-1)
					*/
					while (!op.empty() && priority(op.top()) >= priority(s[i])) {
						if (op.top() == '(') break;   // ( 不参与运算，只作为限界符
						count_push(op.top());
						op.pop();
					}
					op.push(s[i]);
				}
			}
		}
		while (!op.empty()) //[解释]：遍历结束后将栈里的操作符依次全部弹出
		{
			count_push(op.top());
			op.pop();
		}
		return num.top();
	}

private:
	//[作用]：进行栈顶两个数据的运算并压入栈中 
	void count_push(char _operator)
	{
		int tmp = 0;
		int right = num.top();
		num.pop();
		int left = num.top();
		num.pop();
		switch (_operator)
		{
		case '+':
			tmp = left + right;
			break;
		case '-':
			tmp = left - right;
			break;
		case '*':
			tmp = left * right;
			break;
		case '/':
			tmp = left / right;
			break;
		}
		num.push(tmp);
	}

private:
	bool flag = false;   //[作用]：用来标记是否进入左括号
	bool first = true;   //[作用]：用来标记是否是
	stack<int> num;	     //[作用]：存储数据的栈
	stack<char> op;      //[作用]：存储运算符的栈
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112

同时感谢评论区的大神指出这段代码原先的 bug 并提出简洁优雅的解决方案。

小试牛刀

150. 逆波兰表达式求值

224. 基本计算器