随机信号处理AR模型Yule_Walker方程直接解法和Levinson_Durbin递推法的MATLAB与Python实现_yule-walker方程求ar(2)参数r

AR模型

AR模型的系统函数H(z)可以表示为：

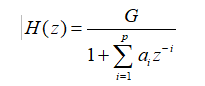
我们的目的就是要求解系统函数的参数a和增益G。

Yule_Walker方程

矩阵形式

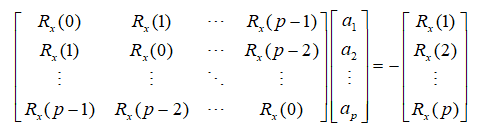
根据生成的矩阵，可以解出p个参数 ，再根据自相关函数，可以求出系统增益G。
Yule_Walker方程也可以写成：

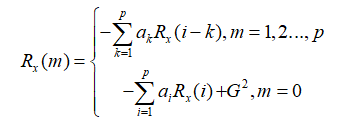
Levinson-Durbin快速递推法

可以看出通过矩阵求逆解Yule-Walker方程的运算量很大，通过观察可以看出Yule_Walker方程的自相关矩阵有一系列良好的性质，可以通过递推的方法求p个参数 ，从而避免矩阵求逆的运算，减少运算量。
令p=1，可以得到1阶AR模型Yule-Walker方程：

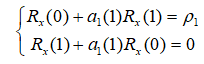
同理，令p=2，3，4…，将不断变化的p用m表示，可以得到m阶AR模型参数Levinson-Durbin递推算法：

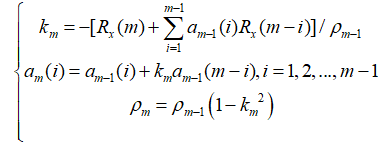
MATLAB实现

Yule_Walker方程

clear
clc
% N = 128;
% p = 64;
N = input('请选择采样点数N:');
p = input('请选择AR模型阶数p（建议N/3<p<N/2):');
n = 0:N-1;
dt = 1;t = n*dt;
xn = 2^0.5*sin(2*pi*0.1*t+pi/3) + 10*sin(2*pi*0.13*t+pi/4); %+ randn(1,N);
R = xcorr(xn,'biased');% 求xn的自相关函数
Rx = zeros(1,p+1);% 预分配内存
% 取对称序列的后半部分
for i = 1:p+1
    Rx(i) = R(i+N-1);
end
Rx
Rmatl = zeros(p,p);
% 生成p个方程对应的矩阵式
for m = 1:p
    for n = 1:p
        Rmatl(m,n) = Rx(max(m,n)-min(m,n)+1);
    end
end
Rmatl
Rmatr = zeros(p,1);
for m = 1:p
    Rmatr(m,1) = -Rx(m+1);
end
% 输出参数ai
ai = (inv(Rmatl)*Rmatr)';% (Rmatl\Rmatr)'
% 根据自相关函数和ai求解系统增益
G = Rx(1);
for i = 1:p
    G = G+ai(i)*Rx(i);
end
fprintf('系统增益G=%f\n',G^0.5);
[H,w] = freqz(G^0.5,[1,ai],N);% 在2*pi范围内N个等分点求系统函数
% Px = (G^0.5)*(abs(H)).^2;
Hf = abs(H);
f = w/(2*pi);
plot(w/(2*pi),Hf);
[magsor,fsor] = findpeaks(Hf,f,'SortStr','descend');% 降序排列
for i = 1:2
    fprintf('预测频率f%d=%f\n',i,fsor(i));
end
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

实验结果

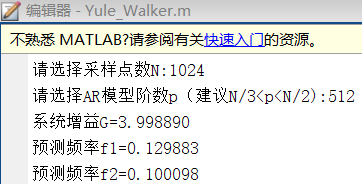
Levinson-Durbin快速递推法

clear
clc
% N = 8;
% p = 4;
N = input('请选择采样点数N:');
p = input('请选择AR模型阶数p（建议N/3<p<N/2):');
n = 0:N-1;
dt = 1;t = n*dt;
xn = 2^0.5*sin(2*pi*0.1*t+pi/3) + 10*sin(2*pi*0.3*t+pi/4);% + randn(1,N);
R = xcorr(xn,'biased');% 求xn的自相关函数
Rx = zeros(1,p+1);% 预分配内存
% 取对称序列的后半部分
for i = 1:p+1
    Rx(i) = R(i+N-1);
end
% 求出1阶AR模型的系数和预测误差功率
a(1,1) = -Rx(2)/Rx(1);
rou(1) = Rx(1)*(1-(a(1,1))^2);
for m = 2:p
    kmsum = 0;
    for i = 1:m-1
        kmsum = kmsum+a(m-1,i)*Rx(m-i+1);
    end
    k(m) = -(Rx(m+1)+kmsum)/rou(m-1);
    a(m,m) = k(m);
    for i = 1:m-1
        a(m,i) = a(m-1,i)+k(m)*a(m-1,m-i);
    end;
    rou(m) = rou(m-1)*(1-(k(m))^2);
end
% rou
% plot(rou)
xlabel('p');ylabel('rou');
G = (rou(p))^2;
[H,w] = freqz(G,[1,a(p,1:p)],N);% 在2*pi范围内N个等分点求系统函数
% Px = (G^0.5)*(abs(H)).^2;
Hf = abs(H);
f = w/(2*pi);
plot(w/(2*pi),Hf);
[magsor,fsor] = findpeaks(Hf,f,'SortStr','descend');% 降序排列
for i = 1:2
    fprintf('预测频率f%d=%f\n',i,fsor(i));
end
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

实验结果

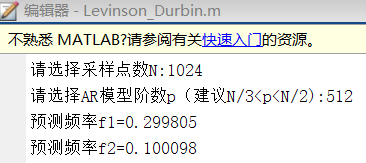
Python实现

Yule_Walker方程

import numpy as np
import scipy.signal
import matplotlib.pyplot as plt
import time

# 定义了寻找峰值的函数，返回值是元素在数组中的位置
def findpeaks(data):
    length = len(data)
    weizhi = []
    for i in range(1,length-1):
        if data[i] > data[i-1] and data[i] > data[i+1]:
            weizhi.append(i)
    return weizhi

# 定义了自相关函数
def xcorr(data):
    length = len(data)
    Rx = []
    datareverse = data[::-1] # 将数组data从后向前取值，每次步进值为1
    Rx = scipy.signal.convolve(data,datareverse)/length # 自相关函数
    return Rx


N = input('请选择采样点数N:') # input输入的N是str类型
p = input('请选择AR模型阶数p（建议N/3<p<N/2):') # 输入阶数
N = int(N) # 把N转换成int类形
p = int(p)
dt = 1
t = np.arange(0,N,dt)# 数组是从0开始的，t=[0 1 2 ... N-1]

# 信号频率
f1 = 0.1
f2 = 0.13
x = np.sqrt(2)*np.sin(2*np.pi*f1*t+(np.pi)/3) + 10*np.sin(2*np.pi*f2*t+(np.pi)/4)# 输入信号
#print(x)
Rx1 = xcorr(x)# 求自相关
Rx = Rx1[N-1:N+p]
#print('Rx=',Rx)

#start = time.clock()
#start = time.perf_counter()
# 生成自相关系数矩阵
Rmatl = np.ones([p,p])
for i in range(0,p):
    for j in range(0,p):
       Rmatl[i][j] = Rx[max(i,j)-min(i,j)]
#print('Rmatl=',Rmatl)

Rmatr = np.ones([p,1])
for i in range(0,p):
    Rmatr[i][0] = -Rx[i+1]
#print('Rmatr=',Rmatr)

# 求系数ai
ai = np.ones([p,1])
Rmatl_inv = np.linalg.inv(Rmatl) # 对左面自相关系数矩阵求逆
ai = np.dot(Rmatl_inv,Rmatr) # 得到各个ai的值
aiT = ai.T # 求ai的转置
#print(aiT)
#end = time.clock()
#end = time.perf_counter()
#print('运行时间=',end-start)

# 求系统增益G
G1 = Rx[0]
for i in range(1,p):
    G1 = G1 + aiT[0][i]*Rx[i]
G = np.sqrt(G1)
#print('系统增益G=',G)

a = np.insert(aiT,0,[1])# 系统函数分母的系数
w,h  = scipy.signal.freqz(G,a,worN = N)
Hf = abs(h)
f = w/(2*np.pi)

plt.plot(f,Hf)
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77

实验结果

Levinson-Durbin快速递推法

import numpy as np
import scipy.signal
import matplotlib.pyplot as plt
import time

# 定义了寻找峰值的函数，返回值是元素在数组中的位置
def findpeaks(data):
    length = len(data)
    weizhi = []
    for i in range(1,length-1):
        if data[i] > data[i-1] and data[i] > data[i+1]:
            weizhi.append(i)
    return weizhi

# 定义了自相关函数
def xcorr(data):
    length = len(data)
    Rx = []
    datareverse = data[::-1] # 将数组data从后向前取值，每次步进值为1
    Rx = scipy.signal.convolve(data,datareverse)/length # 自相关函数
    return Rx

N = input('请选择采样点数N:') # input输入的N是str类型
p = input('请选择AR模型阶数p（建议N/3<p<N/2):') # 输入阶数
N = int(N) # 把N转换成int类形
p = int(p)
dt = 1
t = np.arange(0,N,dt)# 数组是从0开始的，t=[0 1 2 ... N-1]

# 信号频率
f1 = 0.1
f2 = 0.3
# 输入信号
x = np.sqrt(2)*np.sin(2*np.pi*f1*t+(np.pi)/3) + 10*np.sin(2*np.pi*f2*t+(np.pi)/4)
#print(x)
Rx1 = xcorr(x)# 求自相关
Rx = Rx1[N-1:N+p]
#print('Rx=',Rx)

#start = time.perf_counter()
#设定初值
a = np.zeros([p,p])
a[0][0] = -Rx[1]/Rx[0]
rou = np.zeros(p)
rou[0] = Rx[0]*(1-np.square(a[0][0]))
k = np.zeros(p)

#p阶AR模型参数Levinson_Durbin递推算法
for m in range(1,p):
    kmsum = 0
    for i in range(0,m):
        kmsum = kmsum+a[m-1][i]*Rx[m-i]
    k[m] = -(Rx[m+1]+kmsum)/rou[m-1]
    a[m][m] = k[m]
    for i in range(0,m):
        a[m][i] = a[m-1][i]+k[m]*a[m-1][m-i-1]
    rou[m] = rou[m-1]*(1-np.square(k[m]))
#end = time.perf_counter()
#print('运行时间=',end-start)

G = np.sqrt(rou[p-1])
a = np.insert(a[p-1],0,[1])# 系统函数分母的系数
w,h  = scipy.signal.freqz(G,a,worN = N)
Hf = abs(h)
f = w/(2*np.pi)


plt.plot(f,Hf)
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69

实验结果