概率图模型（PGM）：贝叶斯网（Bayesian network）初探_学生george有多大可能从课程

1. 从贝叶斯方法（思想）说起 - 我对世界的看法随世界变化而随时变化

用一句话概括贝叶斯方法创始人Thomas Bayes的观点就是：任何时候，我对世界总有一个主观的先验判断，但是这个判断会随着世界的真实变化而随机修正，我对世界永远保持开放的态度。

1763年，民间科学家Thomas Bayes发表了一篇名为《An essay towards solving a problem in the doctrine of chances》的论文，

这篇论文发表后，在当时并未产生多少影响，但是在20世纪后，这篇论文逐渐被人们所重视。人们逐渐发现，贝叶斯方法既符合人们日常生活的思考方式，也符合人们认识自然的规律，经过不断的发展，最终占据统计学领域的半壁江山，与经典统计学分庭抗礼。

让我们暂时回到Thomas Bayes所处的学术时代18世纪，来一起体会下贝叶斯的思想。

当时数理统计的主流思想是“频率学派”。所谓频率学派，举个例子来说：“有一个袋子，里面装着若干个白球和黑球（例如3黑2白），请问从袋子中取得白球的概率θ是多少？

频率派把需要推断的参数θ看做是固定的未知常数，即概率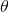虽然是未知的，但最起码是确定的一个值。同时，样本X是随机的，所以频率派重点研究样本空间，大部分的概率计算都是针对样本X的分布。

这种观点看起来确实没有什么问题，也很合理。但是我们仔细深度思考一下就会发现一个重大问题。

频率学派之所以能够得到这种确定性，是因为研究的对象是“简单可数事件”，例如装有固定数量球的袋子、只有正反两面的硬币、只有6面的标准筛子。但是当研究的问题变得复杂之后，频率理论就无法处理了。

例如一个朋友创业，你现在需要估计他创业成功的几率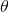有多大？

这个时候你就无法逐一枚举出导致他成功或者失败的所以子原因了（做法有方法？思路清晰？有毅力？能团结周围的人？和其他竞争对手相比，好多少？....），这是一个连续且不可数的事件空间。

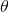
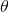
“贝叶斯学派”的观点和频率学派则截然相反，贝叶斯学派认为参数是随机变量，是未知的。而样本X是固定的，由于样本是固定的，所以他们重点研究的是参数的分布。

用贝叶斯学派的理论来回答上面创业者评估问题，假如你对这个创业者为人比较了解，你会不由自主的估计他创业成功的几率可能在80%以上，这是一个先验的概率估计。随着公司的运营，你发现公司被运营的非常差，业绩也不行，随即，你对这个创业者的成功估计由80%下调到40%，这是一个后验概率估计。贝叶斯学派的这种动态的概率估计思维，就是贝叶斯方法。

为了能够动态地对真实世界进行概率估计，贝叶斯及贝叶斯派提出了一个思考问题的固定模式：

先验分布 + 样本信息（观测结果）  后验分布

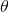
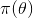
上述思考模式意味着，新观察到的样本信息将修正人们以前对事物的认知。换言之，在得到新的样本信息之前，人们对的认知是先验分布，在得到新的样本信息后，人们对的认知为后验估计。 

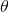
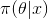
笔者思考：

写到这里的时候，笔者联想到牛顿宏观第一定律和爱因斯坦的相对论之间的关系，在宏观世界，牛顿第一定律是有效的，但是进入高速微观世界，就只能用更抽象的相对论来概括了。牛顿第一定律只是相对论在宏观低速世界的一个特例。

同样，对简单问题来说，因为事件空间有限可数，所以频率理论是成立的，但是对于真实世界的复杂问题，事件空间是连续不可数的，就需要用到贝叶斯理论来概括描述了。

Relevant Link:     

《概率图模型:原理与技术》DaphneKoller 
https://github.com/memect/hao/blob/master/awesome/bayesian-network-python.md

2. 一些背景知识

在本章中，我们回顾一些重要的背景材料，这些材料源自概率论、信息论和图论中的一些关键知识，它们都是贝叶斯网的重要概念组成部分。

0x1：条件概率公式

条件概率（又称后验概率）就是事件A在另外一个事件B已经发生条件下的发生概率。条件概率表示为P(A|B)，读作“在B条件下A的概率”，

• 联合概率：表示两个事件共同发生的概率。A与B的联合概率表示为或者
• 边缘概率（又称先验概率）：是某个事件发生的概率。边缘概率是这样得到的：在联合概率中，把最终结果中那些不需要的事件通过合并成它们的全概率，而消去它们（对离散随机变量用求和得全概率，对连续随机变量用积分得全概率），这称为边缘化（marginalization），比如A的边缘概率表示为P(A)，B的边缘概率表示为P(B)。 

0x2：全概率公式和贝叶斯概率公式

基于条件概率公式，我们可以继续推导出贝叶斯公式。关于这个话题，笔者在另一个文章中进行了详细的总结，这里不再赘述，为了保持文章自包含性，这里摘取部分笔者认为关键的部分。

全概率公式

贝叶斯公式

将其和全概率公式进行对比。会发现以下几点：

• 贝叶斯公式的分子和全概率公式的分解子项是相同的
• 贝叶斯公式的分母等于全概率公式的累加和

笔者认为，贝叶斯公式可以这么理解：贝叶斯公式表达了一个思想，根据某个出现的结果B可以反推所有可能导致该结果的子原因Ai，而具体根据结果B逆推出每个子原因的条件概率比重，则取决于这个子原因和结果B的联合概率 ，这是从结果推原因的逆概率计算问题。

0x3：随机变量的链式法则（chain rule）

根据条件概率的定义，我们有：

更一般地，如果a1，....，a_k是事件，那么有如下链式分解式，

这个等式称为条件概率的链式法则（chain rule）。 换句话说，我们可以将几个事件组合的概率表示为关于事件之间的递归式依赖关系的乘积。值得注意的是，我们可以用事件的任意顺序来扩展这个表达式而保持结果不变。

链式法则是一个非常有用的定理，它是贝叶斯网中的核心概念，因为贝叶斯网面对和描述的都是复杂事件。一个复杂事件往往是由大量子事件组成的，不同的子事件间既存在独立关系，也存在关联依赖关系。链式法则提供了一个理解复杂事件的世界观，即复杂事件是可以分解的。

0x4：随机变量的独立性

关于独立性，有一个很形象直观的例子。假设一个思想实验：如果一个社会中存在一种广泛的思潮，即重男轻女思潮，90%的家庭都认为生男孩比生女孩好，只要生的不是男孩就是继续生，直到生了一个女孩为止。 以上为背景，经过10年后，请问社会中男女比率会失衡吗？

这个问题答案可能有些反直觉，答案是：不管经过多少年，社会中男女比例都保持50%的平衡比例。出现这个现象的原因是，每一胎生男生女都是等概率的，不以父母的意志为转移。

下面我们定义随机变量的独立性概念，

假如或者，则称事件α和事件β，则称事件α和事件β在P中独立，记为。

• 从条件熵的角度解释独立性，事件α和事件β在P中独立，意味着事件事件β对事件α的不确定性不提供额外的信息。
• 从条件概率的角度，我们还可以给出独立性概念的另一种定义，即分布P满足，当且仅当。证明过程如下，
  • 使用链式法则，，由于α和β独立，所以，因此，，所以有，

• • 从该公式可以看到，独立性是一个对称的概念，即意味着。 

我们需要明白的是，在大多数实际的应用中，随机变量并不是边缘独立的，尽管如此，这种方法的一般形式将是我们求解的基础。

0x5：随机变量条件独立性

关于条件独立性，笔者通过一个具体的例子来直观说明。我们假定学生的GPA成绩为随机变量G，被Stanford录入为随机变量S，被MIT录取为随机变量M。很显然，我们会得到下列几个分布判断：

• 零先验下条件依赖：”被MIT录取M“和”被Stanford录取S“之间并不相互独立，如果已知一个学生已经被Stanford录取，那么我们对她被MIT录取的概率的估计就会提高，因为”被Stanford录取S“潜在说明了她是一个智商高有前途的学生。换句话说，”被Stanford录取S“这个事实给”被MIT录取M“输入了额外的有效信息熵。
• 给定额外事件下条件独立：现在假定两所大学仅根据学生的GPA作决定，并且已知学生的GPA是A。在这种情况下，”被Stanford录取S“和”被Stanford录取S“之间就完全独立了。换句话说，在已知GPA的情况下，”被Stanford录取S“对”被Stanford录取S“的推断没有提供任何有效的信息熵，这个现象在贝叶斯网中被称作局部独立性。用条件概率公式表述上面这句话就是，对于这种情况，我们说在给定Grade条件下，MIT与Stanford条件独立。

下面我们形式化地定义事件之间条件独立性的概念，

假如，或者，则称事件α在给定事件Υ时，在分布P中条件独立于事件β，记作。

进一步地有，P满足当且仅当。

现在我们将概念引申到随机变量的范畴内，关注随机变量间的条件独立性。

令X，Y，Z表示随机变量，如果P满足，则称集合X与Y在分布P中条件独立，集合Z中的变量称为观测（observed）变量。观测（observation）这个词很能引起我们的思考，我们看到，在不同的观测下，随机变量的条件独立性发生了改变，这正是体现了贝叶斯思想的精髓。

特别的，如果集合Z是空集，可以把记作，并且称X与Y是边缘独立的（marginally independent）。

0x6：查询一个概率分布

我们基于贝叶斯网进行的一个常见应用是，利用多维随机变量的联合概率分布来完成推理查询。

1. 概率查询

概率查询是最常见的查询，查询由两部分组成，

• 证据（条件）：模型中随机变量的子集E，以及这些变量的实例e
• 查询变量：网络中随机变量的子集Y

概率查询的任务是计算下式：

即，Y的值y上的后验概率分布取决于E=e，这个表达式也可以看作是以e为条件作用获得的分布中Y上的边缘。

2. 最大后验概率（MAP）查询

第二类重要任务是对变量的一些子集找到一个高概率的联合赋值。这类任务的最简单变形是MAP查询（最可能解释MPE），其目的是找到对所有（非证据）变量最可能的赋值。

如果令，那么在给定证据的条件下，我们的任务是为W中的变量找到最可能的赋值：

其中的表示使得最大的值。

0x7：图

把图作为一种数据结构来表示概率分布在贝叶斯网的一个重要概念，我们这节讨论一些图的基本概念。

1. 节点与边

图是一个包含节点（node）集与边（edge）的数据结构。 

假定节点集为，节点对 X_i 与 X_j 由一条有向边（directed edge）X_i -> X_j 或者一条无向边（undirected edge）X_i - X_j 连接。因此，边集是成对节点的集合，图通过二元关系来存所有边的连接关系。

因此，图按照边集的类型，可以分为：

• 有向图（directed graph）：通常记作。
• 无向图（undirected graph）：通常记作，通过忽略边的方向，有向图可以转换为无向图。

我们用来表示 X_i 与 X_j 经由某种边连接的情形，这条边或者是有向的，或者是无向的。

下图是部分有向图的一个例子，

其中，

• A是C的唯一父节点
• F，I 是C的子节点
• C的唯一邻节点是D
• A，D，F，I 均与C相邻

2. 子图

很多时候，我们希望只考虑与节点的特定子集相关的部分图。

1）导出子图

令，且令，导出子图（induced subgraph）定义为图，其中，表示使得的所有边。例如下图表示的是导出子图， 

2）完全子图

如果X中的任意两个节点均由一条边连接，那么X上的子图是完全子图（complete subgraph）。集合X通常称为团（clique）。对于节点的任意超集，如果Y不是团，那么X称为最大团（maximal clique）。

尽管理论上说，节点子集X可以是任意的，但我们一般只对能够保持图结构的特定性质的节点集感兴趣。

3. 路径与迹

利用边的基本符号，可以在图中对不同类型的长范围连接进行定义。

1）路径（path）

对每一个 i=1，...，k-1，如果 X_i -> X_i+1，或者 X_i - X_i+1，那么 X₁，....，X_i 在图中形成了一条路径（path）。如果一条路径中至少存在一个 i，使得 X_i -> X_i+1，则称该路径是有向的。

2）迹（trail）