Lasso回归（概念+实例）

目录

前言

一、基本概念

1.1Lasso回归的起源和动机

1.2数学表达

1.3参数λ的影响

1.4Lasso的计算方法

1.5Lasso与Ridge回归的比较

1.6Lasso的优点和缺点

1.7应用领域

二、具体实例

---

前言

Lasso回归（Least Absolute Shrinkage and Selection Operator，最小绝对收缩和选择算子回归），是一种在统计学中广泛使用的回归分析方法。其核心在于通过对系数进行压缩，以达到变量选择和复杂度调整的目的，从而提高模型的预测精度和解释能力。Lasso回归在处理具有多重共线性数据或者高维数据时尤其有效。

一、基本概念

1.1Lasso回归的起源和动机

Lasso回归由Robert Tibshirani在1996年提出，主要是为了解决传统线性回归在处理高维数据时遇到的问题。在高维空间中，传统的最小二乘法回归（OLS）会出现变量选择困难、模型过拟合等问题。Lasso通过引入一个调整参数（λ），对系数的绝对值进行惩罚，迫使一些不重要的系数值变为零，这样不仅能自动选择重要的特征，还能有效控制模型的复杂度。

1.2数学表达

1.3参数λ的影响

Lasso回归中的λ是一个关键的参数，其值的大小直接影响到最终模型的表现。当λ为0时，Lasso回归就退化为普通的最小二乘回归。随着λ值的增加，越来越多的系数被压缩为零，这有助于特征选择和降低模型复杂度。然而，如果λ过大，它可能会导致模型过于简单，从而影响模型的预测能力。因此，选择一个合适的λ值是实现最佳模型性能的关键。

1.4Lasso的计算方法

Lasso问题的求解通常使用坐标下降法（Coordinate Descent），梯度下降法（Gradient Descent）或者最小角回归法（Least Angle Regression, LAR）等算法。这些算法通过迭代优化来逐渐逼近最优解。

1.5Lasso与Ridge回归的比较

Lasso回归与Ridge回归都是正则化的线性模型。不同之处在于Ridge回归使用L2惩罚项（系数的平方和）进行正则化，而Lasso使用L1惩罚项。L2惩罚倾向于让系数值接近于零但不会完全等于零，适合处理变量间存在较强相关性的情况；而L1惩罚会使某些系数完全为零，从而实现特征的选择。

1.6Lasso的优点和缺点

优点：

• 能有效处理参数的多重共线性问题。
• 通过稀疏解，自动进行变量选择，简化模型。
• 适合用于解析高维数据，其中特征数可能大于样本数。

缺点：

• 当变量数远多于样本数时，Lasso可能不稳定。
• 无法进行群体选择，即相关的变量不会一起被选入或剔除。

1.7应用领域

由于其变量选择和复杂度控制的能力，Lasso回归被广泛应用于诸如生物信息学、金融分析、工业工程等领域，尤其在处理大规模数据集时显示出其优势。

总结来说，Lasso回归是一种强大的统计工具，它通过引入L1正则化惩罚项，帮助构建更简洁、更易解释的模型。正确地选择λ值和理解模型如何通过约束系数来控制复杂度，是使用Lasso回归进行数据分析和预测的关键。

二、具体实例

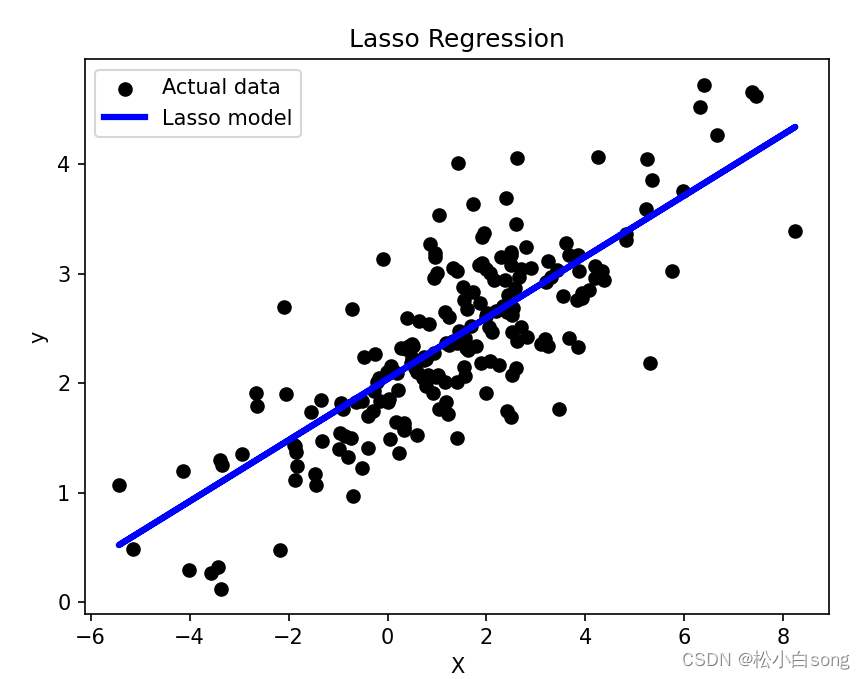
我们首先生成了1000个数据点的输入特征X和对应的输出y，并添加了一些噪声。然后我们把数据分成训练集和测试集，创建了一个Lasso模型，通过调整参数alpha来控制模型的复杂度。最后，我们用均方误差来评估模型的性能，并用图形展示了模型的预测结果与实际数据的对比。

代码：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import Lasso
from sklearn.metrics import mean_squared_error
 
# 生成一些示例数据
np.random.seed(0)
X = 2.5 * np.random.randn(1000) + 1.5   # 生成输入特征X
res = 0.5 * np.random.randn(1000)       # 生成噪声
y = 2 + 0.3 * X + res                   # 实际输出变量y
 
# 将数据分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
 
# 重塑X_train和X_test为正确的形状
X_train = X_train.reshape(-1, 1)
X_test = X_test.reshape(-1, 1)
 
# 创建Lasso回归模型实例
lasso = Lasso(alpha=0.1)
 
# 拟合模型
lasso.fit(X_train, y_train)
 
# 预测测试集的结果
y_pred = lasso.predict(X_test)
 
# 计算并打印均方误差
mse = mean_squared_error(y_test, y_pred)
print("均方误差(MSE):", mse)
 
# 可视化结果
plt.scatter(X_test, y_test, color='black', label='Actual data')
plt.plot(X_test, y_pred, color='blue', linewidth=3, label='Lasso model')
plt.xlabel('X')
plt.ylabel('y')
plt.title('Lasso Regression')
plt.legend()
plt.show()

结果：