深度优先搜索（DFS）（算法笔记）

本文内容基于《算法笔记》和官方配套练题网站“晴问算法”，是我作为小白的学习记录，如有错误还请体谅，可以留下您的宝贵意见，不胜感激。

---

前言

深度优先搜索是一种枚举所有完整路径以遍历所有情况的搜索方法，总是以“深度”作为前进的关键词。实现方式是有很多，最常见的是递归。

---

一、深度优先搜索概述

深度优先搜索属于搜索问题的一种，当问题可以被描述为“路径搜索”时，就可以采用搜素问题的所有解的方式来进行解决，所以DFS本质还是暴力。

深度搜索具有两个关键词，即“岔道口”和“死胡同”，这两个词来源于迷宫问题，这也是搜索问题最原始的表现。当碰到岔道口时，总是以“深度”作为前进的关键词，不碰到死胡同就不回头，因此被称为“深搜”。深搜适合于求解需要遍历所有解或路径的问题，并且剪枝很重要。深搜和广搜在数据结构中的应用就是对非线性存储结构进行遍历。

搜索和分治是两大分析问题的方法，而回溯、剪枝、动态规划可以说是对深度搜索和分治算法进行优化。

二、算法设计

在使用递归进行DFS时，将递归式作为搜索中的“岔道口”，将递归边界作为搜索中的“死胡同”，所以在设计DFS算法时，关键就是找准问题中的“岔道口”和“死胡同”。接下来通过实际例子介绍DFS，这里采用“晴问算法”中的题，书中的例题就不放了。

1.迷宫可行路径数

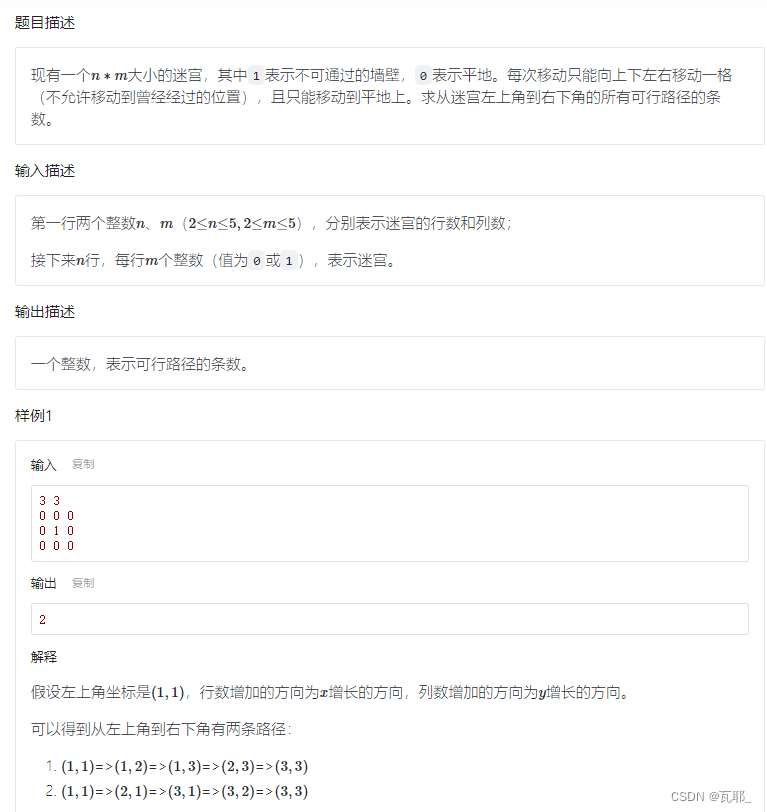
这道题是接下来一系列问题的核心，下面的问题都是基于这道题进行局部修改。
首先分析“岔道口”：
每次移动可以选择上下左右各一格进行移动，也就是说每次有四种选择，即四个岔道口，设当前坐标为（x ，y），四个岔道口的选择就分别为：（x+1，y），（x-1，y），（x，y+1），（x，y-1）。
其次分析“死胡同”：
当搜索到坐标位置元素为1时，表示无法通过，即无法继续搜索，这时这条路径便走到了尽头；当搜索到终点时，就不用继续搜索了。所以一共存在两个递归边界。
接下来就可以设计DFS（）函数：
根据上面“岔道口”的设计，我们需要设置初始状态，即起点。用x表示行坐标，用y表示列坐标，所以函数看起来设这样的：
void DFS(int x , int y , int n , int m){···}，当然，n和m可以放在外面。
递归边界：
if(number[x][y] == 1) return; //死胡同
if(x == n && y == m) { //走到终点
countr++; //计数器
return;
}
岔路口的选择：
需要路径在可移动范围内移动：不允许到曾经到过的地方并且不能出界，所以设置散列表标记曾经走过的位置，注意起点的状态，不论哪条路起点肯定是必须走的。如果满足移动条件，就沿岔路口移动。
完整代码如下：

#include<cstdio>  //迷宫首先要确定起点和终点  
#include<algorithm>
#include<iostream> 
using namespace std;

const int MAXN = 5;
int number[MAXN][MAXN] = {};
int countr = 0;
bool hashTable[MAXN][MAXN] = {true}; //这就不是优化了，如果不设这个条件，就会到达不了递归边界 
//注意起点的状态，肯定要经过起点 
void DFS(int x , int y , int n , int m){
	if(number[x][y] == 1)  return;  //死胡同 
	if(x == n && y == m) {
		countr++;
		return;
	}     //核心：四个岔路口 
	if(x + 1 <= n && hashTable[x + 1][y] == false) { //短路与，顺序也不能乱，不然会报错 
		hashTable[x + 1][y] = true;  //注意一定是先把状态更新，先选上，再走 
		DFS(x + 1 , y , n , m);
		hashTable[x + 1][y] = false; //恢复状态 
	}
	if(x - 1 >= 0 && hashTable[x - 1][y] == false) {
		hashTable[x - 1][y] = true;
		DFS(x - 1 , y , n , m);
		hashTable[x - 1][y] = false;
	}
	if(y + 1 <= m && hashTable[x][y + 1] == false) {
		hashTable[x][y + 1] = true;
		DFS(x , y + 1 , n , m);
		hashTable[x][y + 1] = false;
	} 
	if(y - 1 >= 0 && hashTable[x][y - 1] == false) {
		hashTable[x][y - 1] = true;
		DFS(x , y - 1 , n , m);
		hashTable[x][y - 1] = false;
	}
}

int main(){
	int n , m;
	scanf("%d%d", &n , &m);
	for(int i = 0; i <= n - 1; i++)
		for(int j = 0; j <= m - 1; j++)
			scanf("%d", &number[i][j]);
	DFS(0 , 0 , n - 1, m - 1);
	printf("%d", countr);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

2.指定步数的迷宫问题

这个问题在第一个问题的基础上更改计数器就可以了，相当于新加了一个递归深度的计数器。需要注意的是当存在满足K步的路径时，就不需要继续搜索了，这时直接用回溯算法进行优化，返回上一层。
完整代码如下:

#include<cstdio>  //迷宫首先要确定起点和终点  
#include<algorithm>
#include<iostream> 
using namespace std;

const int MAXN = 5;
int number[MAXN][MAXN] = {};
bool flag = false;
int k;
bool hashTable[MAXN][MAXN] = {true}; //这就不是优化了，如果不设这个条件，就会到达不了递归边界 
//注意起点的状态，肯定要经过起点 

void DFS(int x , int y , int n , int m , int countr){ //countr可以设成参数随搜索动态变化，也可以像hashTable一样恢复状态，就是一个记录递归深度的计数器 
	if(flag) return;
	if(number[x][y] == 1) {  //死胡同
		return;   
	}
	if(x == n && y == m) {
		if(countr == k) flag = true;
		return;
	}     //四个岔路口 
	if(x + 1 <= n && hashTable[x + 1][y] == false) { //短路与，顺序也不能乱，不然会报错 
		hashTable[x + 1][y] = true;  //注意一定是先把状态更新，先选上，再走 
		DFS(x + 1 , y , n , m , countr+1);
		hashTable[x + 1][y] = false; //恢复状态 
	}
	if(x - 1 >= 0 && hashTable[x - 1][y] == false) {
		hashTable[x - 1][y] = true;
		DFS(x - 1 , y , n , m , countr+1);
		hashTable[x - 1][y] = false;
	}
	if(y + 1 <= m && hashTable[x][y + 1] == false) {
		hashTable[x][y + 1] = true;
		DFS(x , y + 1 , n , m , countr+1);
		hashTable[x][y + 1] = false;
	} 
	if(y - 1 >= 0 && hashTable[x][y - 1] == false) {
		hashTable[x][y - 1] = true;
		DFS(x , y - 1 , n , m , countr+1);
		hashTable[x][y - 1] = false;
	}
}

int main(){
	int n , m;
	scanf("%d%d%d", &n , &m , &k);
	for(int i = 0; i <= n - 1; i++)
		for(int j = 0; j <= m - 1; j++)
			scanf("%d", &number[i][j]);
	DFS(0 , 0 , n - 1, m - 1 , 0);
	if(flag == true) printf("Yes");
	else printf("No");
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

3.矩阵最大权值

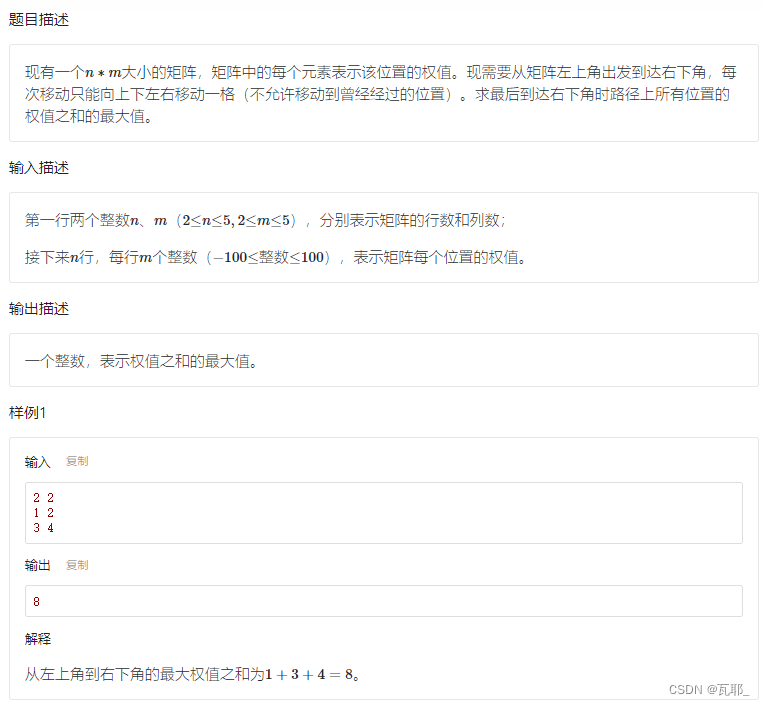
这道题也是加一个计数器就可以了，不过记录的是权值，即坐标位置元素的值。
完整代码如下：

#include<cstdio>  //迷宫首先要确定起点和终点  
#include<algorithm>
#include<iostream> //权值随着搜索而动态改变 
using namespace std;

const int MAXN = 5;
int number[MAXN][MAXN] = {};
int MAX = -10e6;
bool hashTable[MAXN][MAXN] = {true}; //这就不是优化了，如果不设这个条件，就会到达不了递归边界 
//注意起点的状态，肯定要经过起点 
void DFS(int x , int y , int n , int m , int value){
	if(x == n && y == m) {
		if(value > MAX) MAX = value;
		return;
	}     //核心：四个岔路口 
	if(x + 1 <= n && hashTable[x + 1][y] == false) { //短路与，顺序也不能乱，不然会报错 
		hashTable[x + 1][y] = true;  //注意一定是先把状态更新，先选上，再走 
		DFS(x + 1 , y , n , m , value + number[x + 1][y]);
		hashTable[x + 1][y] = false; //恢复状态 
	}
	if(x - 1 >= 0 && hashTable[x - 1][y] == false) {
		hashTable[x - 1][y] = true;
		DFS(x - 1 , y , n , m , value + number[x - 1][y]);
		hashTable[x - 1][y] = false;
	}
	if(y + 1 <= m && hashTable[x][y + 1] == false) {
		hashTable[x][y + 1] = true;
		DFS(x , y + 1 , n , m , value + number[x][y + 1]);
		hashTable[x][y + 1] = false;
	} 
	if(y - 1 >= 0 && hashTable[x][y - 1] == false) {
		hashTable[x][y - 1] = true;
		DFS(x , y - 1 , n , m , value + number[x][y - 1]);
		hashTable[x][y - 1] = false;
	}
}

int main(){
	int n , m;
	scanf("%d%d", &n , &m);
	for(int i = 0; i <= n - 1; i++)
		for(int j = 0; j <= m - 1; j++)
			scanf("%d", &number[i][j]);
	DFS(0 , 0 , n - 1, m - 1 , number[0][0]);
	printf("%d", MAX);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

4.矩阵最大权值路径

这道题可以开数组记录走过的坐标，并设置最大权值之和路径数组，如果权值之和更大，交换数组。注意更新数组状态，不要影响其他路径的选择。
完整代码如下：

#include<cstdio>  //迷宫首先要确定起点和终点  
#include<algorithm>
#include<iostream> //权值随着搜索而动态改变 
#include<vector>//这里也不知道开多长，就用vector实现吧 , 这道题是前面的整合,走一步记一下，如果权值更大，更新结果数组 
using namespace std;
const int MAXN = 5;
int number[MAXN][MAXN] = {};
int MAX = -10e6;
vector <int> temp , ans;
bool hashTable[MAXN][MAXN] = {true}; //这就不是优化了，如果不设这个条件，就会到达不了递归边界  
//注意起点的状态，肯定要经过起点 
void DFS(int x , int y , int n , int m , int value){
	if(x == n && y == m) {
		if(value > MAX) {
			MAX = value;
			ans = temp;
		}
		return;
	}     //核心：四个岔路口 
	if(x + 1 <= n && hashTable[x + 1][y] == false) { //短路与，顺序也不能乱，不然会报错 
		hashTable[x + 1][y] = true;  //注意一定是先把状态更新，先选上，再走 
		temp.push_back(x + 1); 
		temp.push_back(y); 
		DFS(x + 1 , y , n , m , value + number[x + 1][y]);
		hashTable[x + 1][y] = false; //恢复状态 
		temp.pop_back();
		temp.pop_back();
	}
	if(x - 1 >= 0 && hashTable[x - 1][y] == false) {
		hashTable[x - 1][y] = true;
		temp.push_back(x - 1) ; 
		temp.push_back(y);
		DFS(x - 1 , y , n , m , value + number[x - 1][y]);
		hashTable[x - 1][y] = false;
		temp.pop_back();
		temp.pop_back();
	}
	if(y + 1 <= m && hashTable[x][y + 1] == false) {
		hashTable[x][y + 1] = true;
		temp.push_back(x) ; 
		temp.push_back(y + 1);
		DFS(x , y + 1 , n , m , value + number[x][y + 1]);
		hashTable[x][y + 1] = false;
		temp.pop_back();
		temp.pop_back();
	} 
	if(y - 1 >= 0 && hashTable[x][y - 1] == false) {
		hashTable[x][y - 1] = true;
		temp.push_back(x) ; 
		temp.push_back(y - 1);
		DFS(x , y - 1 , n , m , value + number[x][y - 1]);
		hashTable[x][y - 1] = false;
		temp.pop_back();
		temp.pop_back();
	}
}

int main(){
	int n , m;
	scanf("%d%d", &n , &m);
	for(int i = 0; i <= n - 1; i++)
		for(int j = 0; j <= m - 1; j++)
			scanf("%d", &number[i][j]);
	temp.push_back(0);temp.push_back(0);  
	DFS(0 , 0 , n - 1, m - 1 , number[0][0]);
	for(vector<int> :: iterator it = ans.begin(); it != ans.end(); it = it + 2){  //迭代器遍历
		printf("%d %d\n", *it + 1 , *(it + 1) + 1);
	}
		
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70

三、备注

1.递归只是一种实现方法，分治法和搜索都可以采用递归实现，且相对其他方法更简单，只是运行效率低且容易爆站，所以需要算法优化；
2.分治法和搜索虽然实现方式都是递归，但在分析问题时是两种不同的是思想；
3.回溯优化是指当递归满足某些条件时就可以停止递归返回上一层，所以回溯的前提是必须存在可行解保证可以走到递归边界，否则会死递归；
4.剪枝优化是指在面对岔路口时，在满足某些条件时，可以减少岔路口的选择；
5.注意优化和递归边界的区别，递归边界是问题必须满足的最后条件，而优化是在题目条件的限制上来减少计算量；
6.搜索算法并不只存在于数据结构的图论中，虽然最初接触DFS和BFS时是在数据结构中，但实际这是一种算法，当问题满足可以搜索的性质时，就可以运用搜索算法；
7.注意递归中参数的作用域；
8.全排列适合用分治解决，组合适合用搜索解决；