孟德尔随机化（一）| 随处可见的孟德尔随机化到底是什么？

近来咱们的各大群中，经常有小伙伴们会问到孟德尔随机化相关的问题，鉴于它的出现频率过高，咱们就不得不来唠唠喽！

这个系列我们会详细介绍孟德尔随机化的基本原理、分析流程、结果解读、文献解析其及优势和局限性等等。

看到孟德尔随机化，大家肯定第一时间想到孟德尔！毕竟小时候的我们都学过，孟德尔种豌豆的故事！它们之间有什么联系吗？那必须有！请往下看！

众所周知，在1854年的夏天，我们圣托马斯修道院的院长孟德尔，开启了他的豌豆实验，他通过小小的豌豆进行了一系列杂交实验，最终提出了遗传学的两个基本定律 —— 分离定律和自由组合定律，统称为孟德尔遗传规律。不过，孟德尔定律只适用于单基因的遗传性状，并且无法解释复杂的多基因遗传疾病。此外，孟德尔定律也无法解释环境因素对基因表达的影响，以及基因与环境的相互作用。为了解决这个问题，著名统计学家Fisher提出了 孟德尔随机化（Mendelian Randomization，MR） 的概念。

就是那个Fisher精确检验的那个Fisher！想不到吧！太酷了！

MR 是一种基于遗传变异的因果推断方法，其基本原理是利用自然界中的随机分配的基因型对表型的影响来推断生物学因素对疾病的影响。咱们接下来就给它掰开了揉碎了唠唠！

前情提要来一波

传统的观察性研究中，潜在混杂和反向因果关系会影响其因果推断能力。**孟德尔随机化（Mendelian Randomization，MR）是工具变量（instrumental Variable，IV）**分析的一种类型，它使用遗传变异作为 IV 来检测和量化因果关系。由于能克服潜在混杂和反向因果关系的影响，近年来 MR 在观察性研究中的应用越来越广泛。早期的 MR 研究通常在小样本人群中进行，且仅使用了少量的遗传变异，这就使得 MR 研究效力较低。随着生物学界发现了大量与特定性状紧密相关的遗传变异，加上许多大样本全基因组关联研究（Genome-Wide Association Study，GWAS）公开发布了数十万个暴露和疾病与遗传变异关系的汇总数据，这一领域发生了一场革命。这些汇总数据使得研究者能估计大样本数据中的遗传关联，从而促进了 MR 研究发展。

看看近年来关于孟德尔随机化研究的数量！影响因子还不低的嘞！

近年来，该领域在方法学上也迅速更新，新方法克服了传统 MR 方法的一些特定限制，但其同样存在局限性。我们只有正确了解 MR 背后的原理、局限性及不同方法的适用条件才能针对不同的研究问题和特定的数据正确应用 MR。

那，咱们开始！孟德尔随机化！挖挖挖！

什么是孟德尔随机化

上面我们提到，孟德尔随机化（Mendelian Randomization，MR）是一种基于遗传变异的方法，用于推断因果关系。

该方法利用与暴露密切相关的遗传变异（通常以单核苷酸多态性（Single Nucleotide Polymorphism，SNP）的形式）作为工具变量（Instrumental Variable，IV），通过遗传变异的特性来评估暴露因素与结局之间的因果关系。

在这里，我们使用“暴露”一词来指代假定的因果风险因素，有时也称为中间表型，它可以是生物标志物（Biomarker）、人体测量指标（Physical Measurement）或任何其他可能影响结果的风险因素（Risk Factor）。通常情况下，结局是疾病，但并不局限于疾病。

为什么使用孟德尔随机化

咱们举个大例子帮助大家理解！

假如我们想要研究肥胖（也就是我们前面提到的暴露因素）和二型糖尿病之间的关系，通常情况下我们会如何进行研究呢？

我们是不是可能会通过对比肥胖人群和无肥胖人群发生二型糖尿病的概率来进行推断。假如我们发现肥胖人群中患二型糖尿病的概率确实显著较高，那这样我们就能说明肥胖是二型糖尿病的风险因素了吗？

NONONO！！！请看下图和下文！

当然不能啦！这只能说明肥胖和二型糖尿病这两种情况共同发生的概率较高，并不能说明肥胖就是二型糖尿病的风险因素。因为除了肥胖，可能还有其他因素也会导致二型糖尿病的发生，比如肥胖是不是可能通过影响到血压、血脂、胰岛素抵抗等指标进而导致了二型糖尿病的发生呢？再比如如果是二型糖尿病导致了肥胖，而不是肥胖导致了二型糖尿病呢？那这样我们依然会观察到，肥胖人群患二型糖尿病的风险较高的现象。

其实，这就是混杂因素和反向因果的影响。那怎么嘞！铛铛铛！铛！孟德尔随机化驾到！通通闪开！

让我们来看看孟德尔随机化是如何解决这些问题的！

为了克服混杂和反向因果关系的影响，孟德尔随机化引入了遗传变异作为工具变量进行分析。但是这些遗传变异是需要满足一些条件的！

首先这些遗传变异需要和肥胖的发生有很强的关联，只有这样，我们才能利用这些遗传变异数据来替代肥胖这个暴露因素。

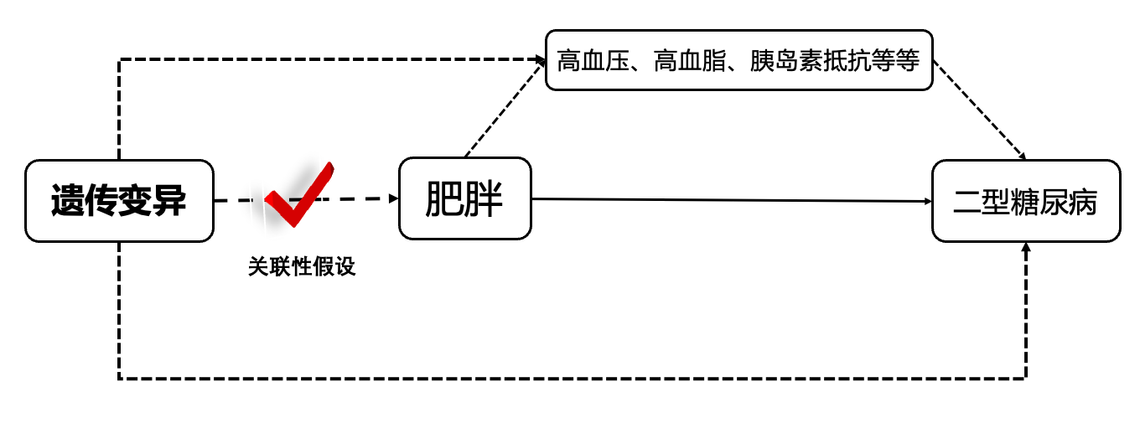
与此同时，这个遗传变异还不能与血压、血脂、胰岛素抵抗等这些混杂因素有关联，否则的话，这些遗传变异是通过影响肥胖还是其他因素导致的二型糖尿病就不好解释啦！

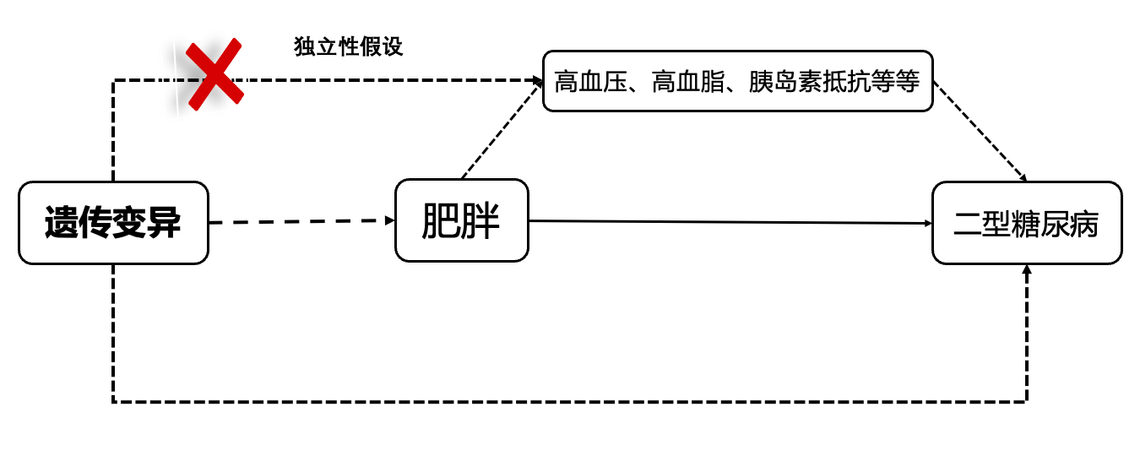
还有，这些遗传变异还不能和二型糖尿病直接关联，如果它们能够直接导致二型糖尿病的话，那岂不是就和肥胖没有关系了嘛！这不就偏离了我们的设计初衷嘛！

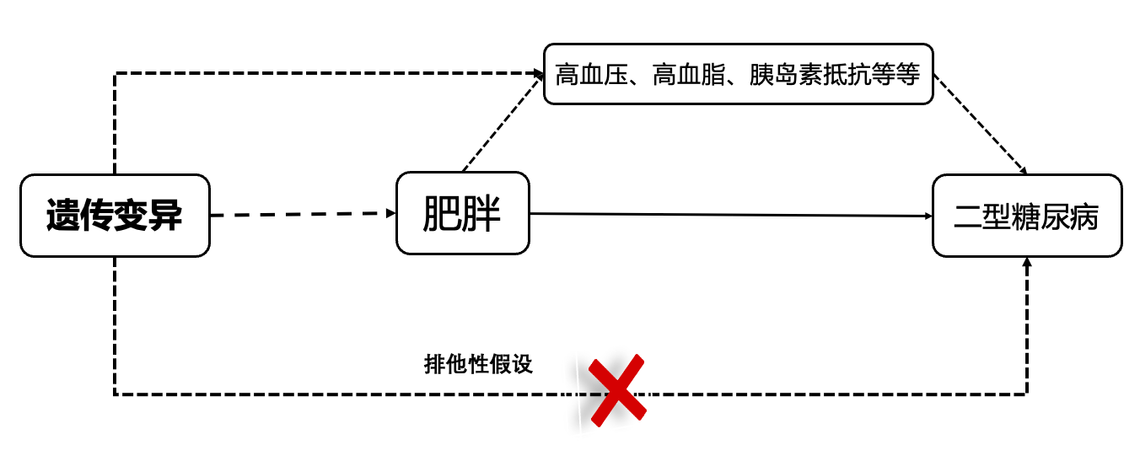
综上！同时满足这三个条件的遗传变异，我们才可以把它们当作肥胖的工具变量，进而替代肥胖，以研究肥胖与二型糖尿病的发生是否有关联。

这就是孟德尔随机化的三大基本假设啦！我们总结一下！

三大核心假设

通过上面的例子，我们可以总结出孟德尔随机化需要满足的基本假设啦！

1. 关联性假设：工具变量（遗传变异）必须与暴露因素之间存在稳定的强相关关系，弱工具变量（也就是相关关系较弱的工具变量）的使用会导致估计出现偏倚。在上面的例子中就是选择的遗传变异与肥胖的发生一定要密切相关。
2. 独立性假设：工具变量与影响“暴露-结局”关系的混杂因素相互独立。在上面的例子中就是遗传变异与肥胖导致的高血压、高血脂、胰岛素抵抗等因素或者其他因素要相互独立，没有相关性。
3. 排他性假设：除了通过暴露的途径，遗传变异与结局变量之间没有其他独立的因果途径，也就是遗传变异只能通过暴露因素对结局产生影响，而不能通过其他途径对结果产生作用。在上面的例子中就是那个SNP只能通过影响肥胖来导致二型糖尿病，不能有其他影响途径。

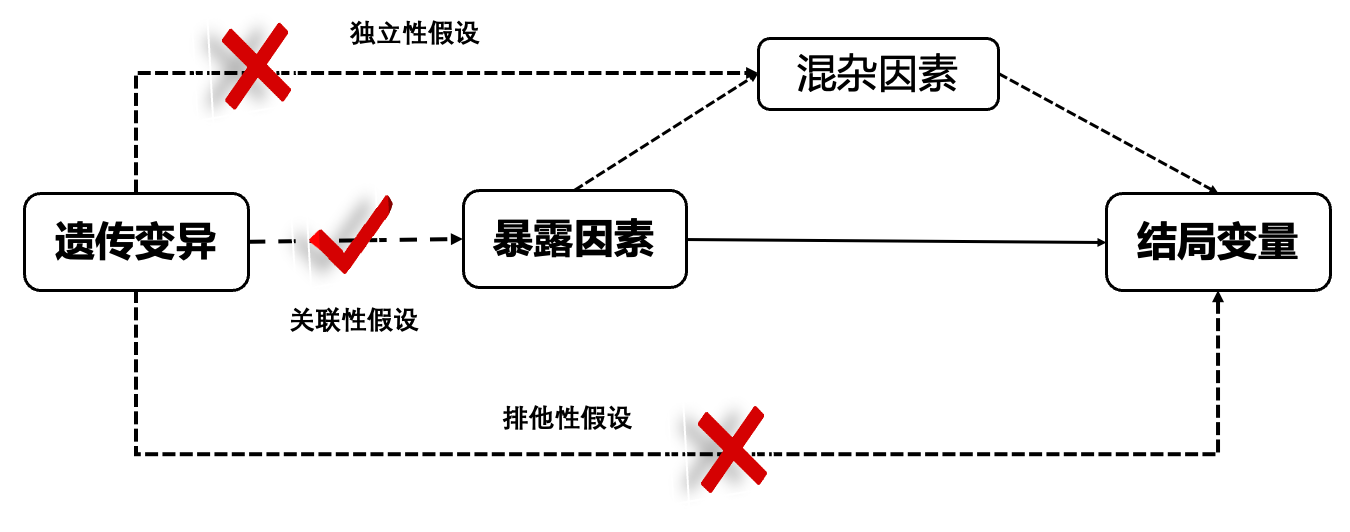
混杂因素和反向因果

我们还是看上面提到的肥胖与二型糖尿病关系研究的例子！

同时满足这三个条件的遗传变异，我们才可以把它们当作肥胖的工具变量，进而替代肥胖，以研究肥胖与二型糖尿病的发生是否有关联。

这里提到的“同时满足这三个条件的遗传变异”，满足满足排他性假设，只能通过影响肥胖进而影响二型糖尿病的发生，所以可以排除混杂因素的影响。

又因为这些遗传变异是在受精过程完成之后就确定了的，不会受到二型糖尿病的影响，所以反向因果关系也不会存在。

所以如果这些遗传变异和二型糖尿病的发生确实有关联，这也就意味着肥胖的确和二型糖尿病的发生有关联。

我们总结一下！
为什么孟德尔随机化可以克服混杂和反向因果关系的影响呢？

在孟德尔随机化框架中，基因型（由遗传变异决定）在减数分裂期间随机分配给后代，这种随机分配使得在大规模群体中，基因型与通常困扰观察性流行病学研究的干扰因子基本无关。此外，种系遗传变异（也就是可遗传的变异）在受孕时被暂时固定，不会因任何结果或疾病的发生而改变，从而排除了反向因果关系的可能性。

此外，鉴于现代基因分型技术的改进，遗传数据的测量误差和系统性错误分类通常较低。因此，孟德尔随机化可以被认为类似于“自然的随机对照试验”。

遗传变异作为工具变量的优势

1. 由孟德尔第二定律可知，一个性状的遗传独立于其他性状的遗传且呈现随机性，因此后代基因型不太可能与人群中的环境混杂因素相关。

2. 基因型分布在时间上先于后天暴露，基因型与疾病之间的联系不会受到反向因果关系的影响。

3. 与暴露相关的基因型通常从出生到成年都与之相关，因此，在因果推断中可避免因误差而造成的衰减（回归稀释偏倚）。

   回归稀释偏倚是指在进行回归分析时，若一个解释变量与被解释变量之间存在第三个变量（即控制变量）的干扰，会导致原本两个变量之间的关系被稀释或掩盖。这种偏倚可能会让我们无法准确地评估两个变量之间的真实关系。

   举个小栗子：假设我们想研究体重和身高之间的关系，我们发现身高与体重正相关，即身高增加时体重也会增加。然而，这个关系可能被饮食习惯作为控制变量的干扰所稀释。如果我们没有将饮食习惯作为控制变量加以考虑，那么体重与身高的关系可能会被掩盖，以至于我们不能准确地判断身高对于体重的影响。

   所以，回归稀释偏倚提醒我们在进行回归分析时要注意可能存在的干扰变量，应该通过控制这些干扰变量来准确地评估解释变量和被解释变量之间的关系。

4. 这一定律在人群中是普遍存在的，避免了随机对照试验（Randomized Controlled Trials，RCT）中的研究性对象代表性问题。

5. 并不一定要找到因果 SNP，一个与因果 SNP 处于连锁不平衡（Linkage Disequilibrium，LD）的SNP即可满足假设条件。

6. 在 GWAS 和高通量基因组技术的时代，人群遗传数据通常可方便地从大型公开数据库中获得。

7. ……

下次介绍孟德尔随机化的分析流程！

---

那今天的分享就到这里啦！我们下期再见哟！

最后顺便给自己推荐一下嘿嘿嘿！

如果我的分享对你有用的话，欢迎关注点赞在看转发分享阿巴阿巴阿巴阿巴巴巴！这可是我的第一原动力！

蟹蟹你们的喜欢和支持！！！

啊对！如果小伙伴们有需求的话，也可以加入我们的交流群：一定要知道 | 我们的生信交流群终于来啦！

还有兴趣的话，也可以看看我掏心掏肺的干货满满 | 给生信小白的入门小建议 | 掏心掏肺版！绝对干货满满！

后续这个链接可能会更新，如果小伙伴点开它之后发现，咦，怎么失效啦！不要慌！咱们辛苦一下动动小手去公众号主页的作者精选那里，会有一篇同名的文章，点进去就是啦！

参考资料

1. https://www.bilibili.com/video/BV1oN411y7kf/
2. https://zhuanlan.zhihu.com/p/383529186
3. https://zh.wikipedia.org/zh-cn/孟德爾隨機化
4. 于天琦,徐文涛,苏雅娜等.孟德尔随机化研究基本原理、方法和局限性[J].中国循证医学杂志,2021,21(10):1227-1234.
5. https://zhuanlan.zhihu.com/p/125153774
6. https://zhuanlan.zhihu.com/p/643496483