- 1Flutter TextField实现双向绑定_flutter textfield 双向绑定
- 2NLP:自然语言生成中的top-k, top-p, typical采样方法的实现_topp采样
- 3【AI视野·今日NLP 自然语言处理论文速览 第二十三期】Tue, 28 Sep 2021_ccbert
- 4人工智能与云计算:如何实现医疗数据的高效共享_医疗云下患者的数据共享模式
- 5计算机视觉算法 面试必备知识点(2022)_计算机视觉算法 面试必备知识点(2022)_视觉算法面试_奶盖芒果的博客-csdn博客
- 6综述:自动驾驶中的多模态 3D 目标检测_mvxnet解析
- 7鸿蒙应用开发 | 最牛逼的 自定义 布局_鸿蒙 getestimatedheight
- 8GitOps 实操手册 1: 应用程序容器化_gitops 方案
- 9MATLAB非线性优化函数总结(二)_matlab中的objfun函数
- 102024年03月CCF-GESP编程能力等级认证C++编程二级真题解析
注意力机制(attention)和自注意力机制(self-attention)_selfattention temper
赞
踩
本文参考了b站博主蘅芜仙菌的视频以及文章Transformer:注意力机制(attention)和自注意力机制(self-attention)的学习总结
如有侵权,联系删除。
注意力机制其实是源自于人对于外部信息的处理能力。由于人每一时刻接受的信息都是无比的庞大且复杂,远远超过人脑的处理能力,因此人在处理信息的时候,会将注意力放在需要关注的信息上,对于其他无关的外部信息进行过滤,这种处理方式被称为注意力机制。
针对于注意力机制的引起方式,可以分为两类,一种是非自主提示,另一种是自主提示。其中非自主提示指的是由于物体本身的特征十分突出引起的注意力倾向,自主提示指的是经过先验知识的介入下,对具有先验权重的物体引起的注意力倾向。换句话说,可以理解为非自主提示源自于物体本身,而自主提示源自于一种主观倾向。
一、注意力机制
Self-Attention是个啥,自己注意自己?Q、K、V又是什么?为什么它们要叫query、key、value,它们有啥关系?
先来看一个问题,假设我们现在有一个键值对(Python字典),如下图所示。现在我给出一个人的腰围为57,想要预测其体重。自然地,我们推断其体重在43~48之间,但是我们还需要定量计算体重预测值,由于57到56、58的距离一样,所以一种方法是取它们对应体重的平均值。
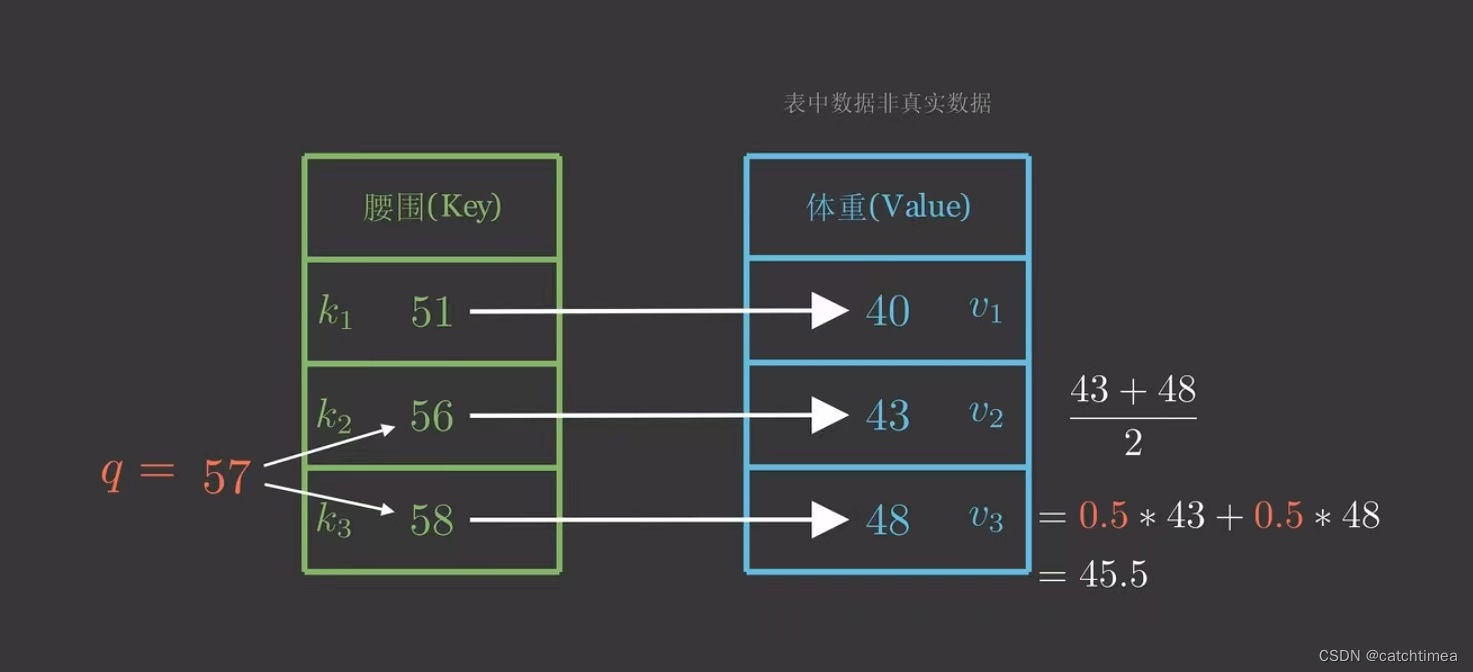
因为57距离56、58最近,我们自然会非常“注意”它们,所以我们分给它们的注意力权重各为0.5,不过我们没有用上其他的(Key,Value),似乎我们应该调整一下注意力权重,但权重如何计算?
假设用 来表示 q 与 k 对应的注意力权重,则体重预测值
为:

是任意能刻画相关性的函数,但需要归一,称作评分函数。我们以高斯核(注意力分数)为例(包括softmax函数):
通过这种方式我们就可以求得体重估计值,这也就是注意力机制(Attention)。所以我们把上面的q叫做query(请求),k叫做key(键),v叫做value(值)。
因此总结出通用的注意力机制公式为:
q、k、v都为多维的情况也是类似的。假设现在给出的q是二维的,由于 q1 和 k1 都是二维向量,注意力分数 可以是以下几种:
(1) 加性模型:
加性注意力机制一般是用来处理query和key的向量维数不一致的情况。可以从向量相加来理解,当向量q和向量k越接近,两个向量相加的结果就越大,那么加性注意力获得的权重就越大,反之两个向量离得越远则相加的结果越小,加性注意力获得的权重就会越小。
(2) 点积模型:
点积注意力相比于加性注意力,其计算效率更高,但是要求query和key的向量维数必须一致。从点积公式上理解,点积公式为 。从公式中可以看出如果两个向量越近,则
越大,点积值越大。因此,注意力的权重就越大。反之,如果两个向量离的越远,则
就越小,点积值越小,从而注意力的权重就越小。
我们以点积模型为例,为了方便我们用矩阵来表示,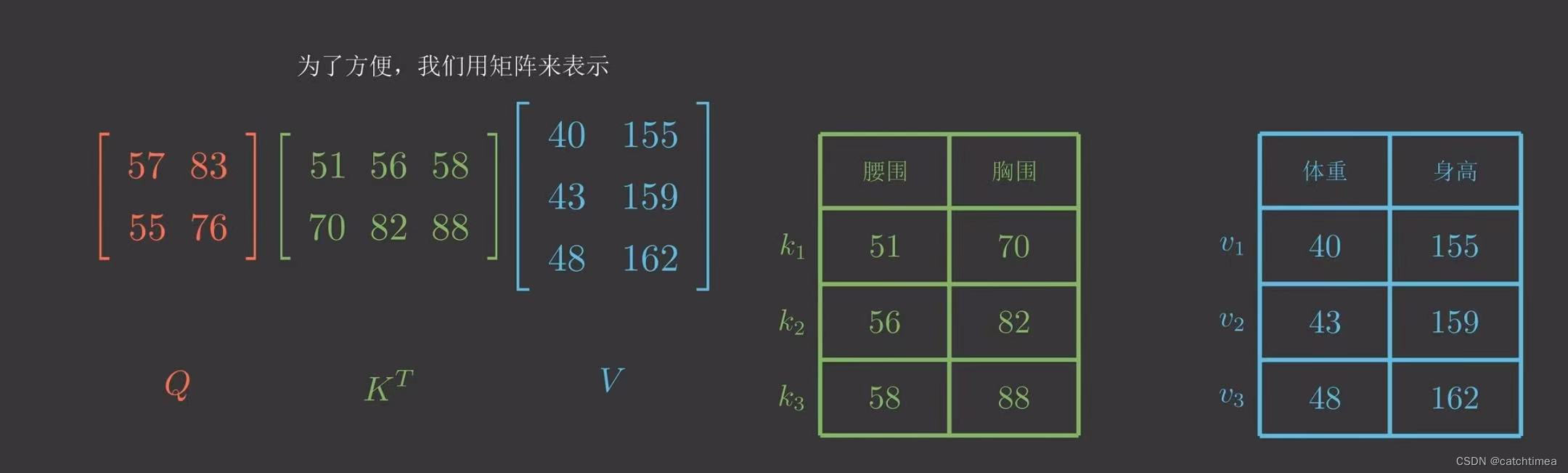
为了缓解梯度消失的问题我们还会除以一个特征维度。。
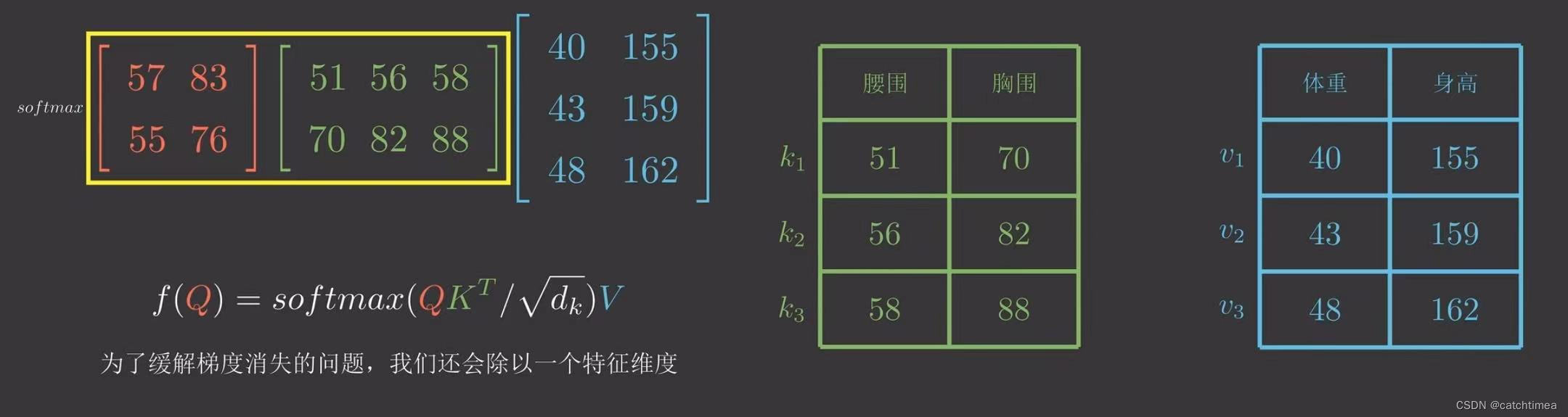
值得一提的是softmax是吃一个向量吐一个向量。而这里的softmax吃的是一个矩阵,因此实际上是对矩阵中的每一行进行softmax。(沿着每个数据的特征维度做softmax操作可以使其特征更加鲜明)
二、自注意力机制
如果Q、K、V是同一个矩阵会发生什么?没错,那就是大名鼎鼎的自注意力机制。我们用X来表示这个矩阵,则可以表示为如下式子:

但在实际应用中可能对X先做不同的线性变换再输入,比如变形金刚(Transformer)模型。

这可能是因为X转换空间后能更加专注注意力的学习。
自注意力机制和注意力机制的区别就在于,注意力机制的查询和键是不同来源的。
例如,对于注意力机制。在Encoder-Decoder模型中,键是Encoder中的元素,而查询是Decoder中的元素。在中译英模型中,查询是中文单词特征,而键则是英文单词特征。而自注意力机制的查询和键则都是来自于同一组的元素。
而对于自注意力机制来说,在Encoder-Decoder模型中查询和键都是Encoder中的元素,即查询和键都是中文特征,相互之间做注意力汇聚。也可以理解为同一句话中的词元或者同一张图像中不同的patch,这都是一组元素内部相互做注意力机制。因此,自注意力机制也被称为内部注意力机制。
个人理解:自注意力机制的作用是学习query对其他所有key的依赖关系。即每个特征信息都是组内其他所有特征信息的关系组合。举例说明:
在一句话中,通过自注意力机制可以使每个单词不光包含自己的主题信息,还可包含和其他单词的关系信息(主谓,指代等)。因此,每个单词都具备和其他单词的依赖关系。再从图像中来讲,每个patch(图像会划成不同的块,每个块称为patch)都可包含和其他patch的关系信息,也可以理解为建立了全局感受野。
自注意力机制的优缺点
- 优点:可建立全局的依赖关系,扩大图像的感受野。相比于CNN,其感受野更大,可以获取更多上下文信息。有论文论证了自注意力机制比卷积可以获得更大的感受野,这对语义分割任务十分有效。
- 缺点:自注意力机制是通过筛选重要信息,过滤不重要信息实现的。这就导致其有效信息的抓取能力会比CNN弱一些。之所以这样是因为自注意力机制相比CNN,无法利用图像本身具有的尺度、平移不变性以及图像的特征局部性(图片上相邻的区域有相似的特征,即同一物体的信息往往都集中在局部)这些先验知识,只能通过大量数据进行学习。这就导致自注意力机制只有在大数据的基础上才能有效地建立准确的全局关系,而在小数据的情况下,其效果不如CNN。
综上所述,Self-Attention自注意力机制是Attention的进化形式。Self-Attention只关注输入序列元素之间的关系。通过将输入序列直接转化为Q、K、W,在内部进行Attention计算,能够很好地捕捉文本的内在联系,对其做出再表示。
另一种进化形式Multi-Head Attention,则是在自注意力机制的基础上使用多种变换生成的Q、K、V进行运算,再将它们对相关性的结论综合起来,进一步增强Self-Attention的效果。
简单来说,单一注意力汇聚只会建立一种查询和键的依赖关系。而我们常希望可以基于相同的注意力汇聚方法学习到不同的依赖关系,即拥有捕获序列内各种依赖关系的能力。例如机器翻译任务,以“I like fishing because it can relax my mind"要翻译为”我喜欢钓鱼因为可以放松心情“为例。我们以”放松“为query,对英文句子中每个单词的key进行注意力汇聚,结果获取 ”放松“ 和 ”relax“ 的关系,这是单头注意力的结果。如果我们进行多次注意力汇聚,则就可能获取到 ”放松“ 和 ”fishing“、”I“ 等单词的依赖关系。这样,我们将多个结果进行融合就可以得到更为全面复杂的依赖关系。这对于深度学习下游任务,例如目标检测、语义分割等都具有很大帮助。这就是要介绍的多头注意力汇聚方法。具体流程如下:
(1)首先,将查询、键和值通过多组全连接层来获取对应的特征向量。由于每个全连接层的参数都是可学习的。因此,经过独立学习可以获取多组不同特征的查询、键和值的特征向量。
(2)然后,对多组查询、键和值的特征向量进行注意力汇聚,从而获得多个不同注意力汇聚运算结果。
(3)最后,将所有的注意力汇聚运算结果进行拼接,再经过一个全连接层就可映射出所需的最后输出。
# 其中每一个注意力汇聚都被称作一个头(head)。由于有多个注意力汇聚,因此才被称作多头注意力。
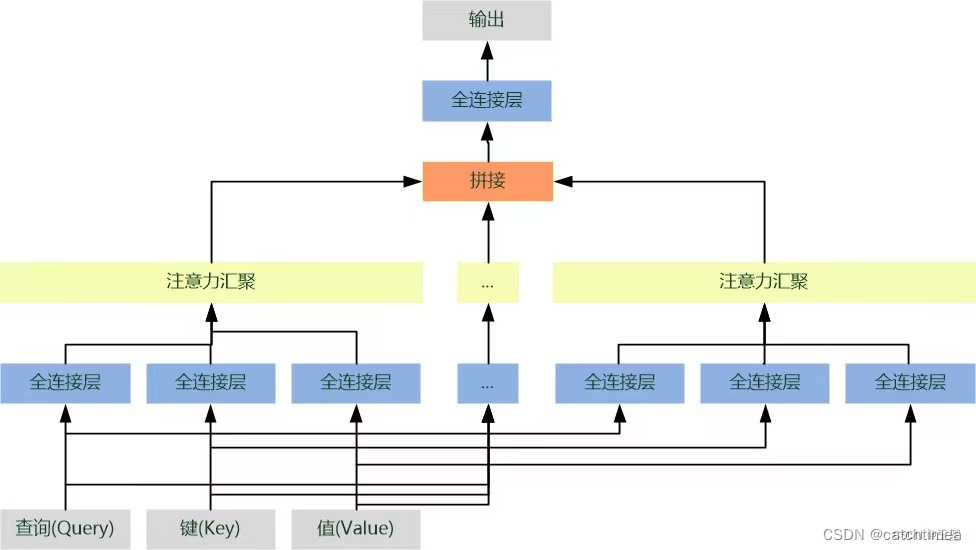
单一自注意力机制示例
假设对deep learning这个词组做单头的注意力机制,原理如下图所示:
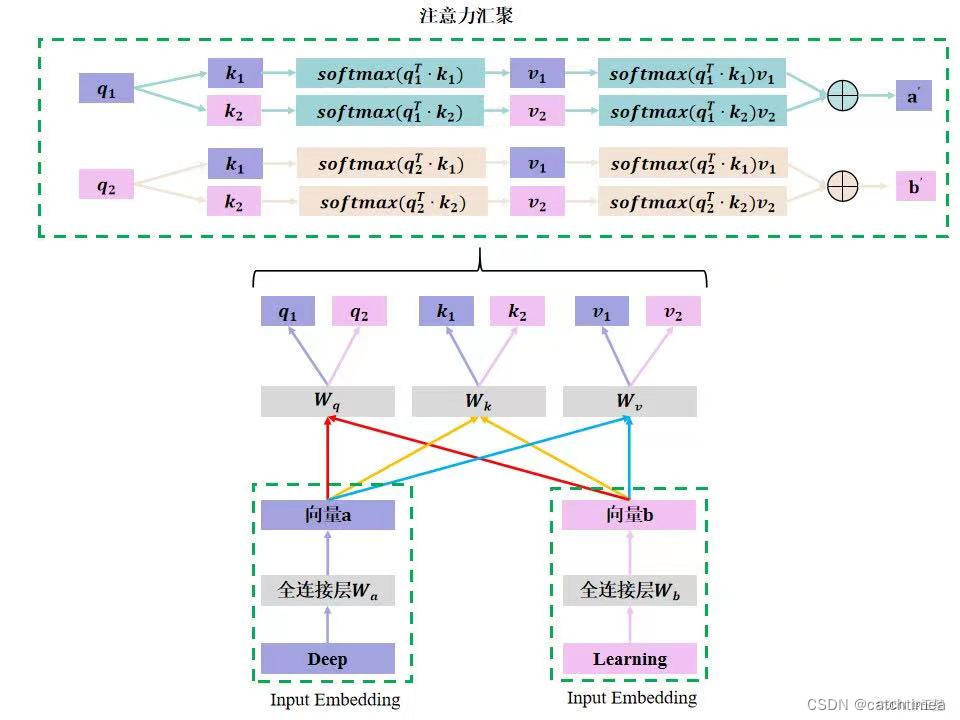
注意:
- 向量 是Deep单词经过全连接层
得到的,向量
是Learning单词经过全连接层
得到。
- 向量 、
分别是向量
、
经过全连接层
得到的。
,
,
,
同理。
- 向量 、
分别是向量
、
经过注意力汇聚后的结果。
多头自注意力机制示例
假设对Deep Learning这个词组做多头注意力机制(两头)原理如下图所示:
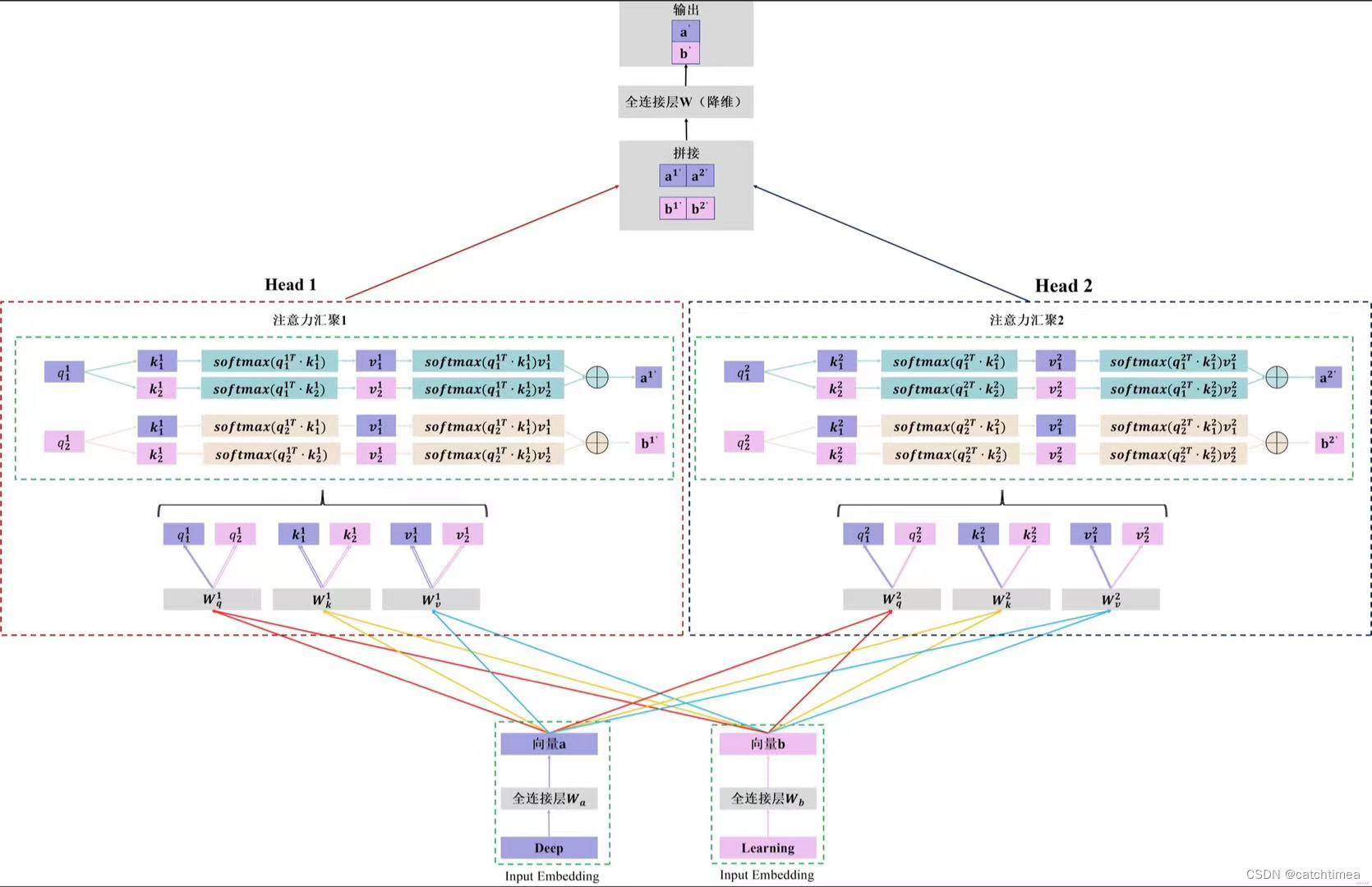
总 结
(1)注意力可以分为两种方式分别是自主提示和非自主提示。其中非自主提示是键,自主提示是查询,物体原始向量是值。键和值是一一对应的。
(2)注意力机制的评分函数可以对查询和键进行关系建模,获取查询和键的相似度匹配。其方法分为两种:加性注意力和点积注意力。常用的是点积注意力。
(3)如果查询和键是同一组内的特征,并且相互做注意力机制,则称为自注意力机制或内部注意力机制。
(4)多头注意力机制的多头表示对每个Query和所有的Key-Value做多次注意力机制。做两次,就是两头,做三次就是三头。这样做的意义在于获取每个Query和所有的Key-Value的不同的依赖关系。
(5)自注意力机制的优点是感受野大;缺点是需要大数据。



