- 1LeetCode哈希表篇【两数之和】_两数之和 力扣题目链接 (opens new window) 给定一个整数数组 nums 和一个目
- 2SpringBoot面试题 44道
- 318款顶级开源与商业流分析平台推荐与详解
- 4数据挖掘复习笔记-3.数据预处理实例_labormissing.txt
- 5k8s资源监控_bitnami metrics-server v0(1),2024一位Linux运维中级程序员的跳槽面经
- 6大数据复习(第五六章)_大数据lp
- 7手把手教你使用 IDEA 连接 kingbase 人大金仓数据库(2024最新)_idea database连接kingbase8
- 8Matlab|基于蒙特卡洛的风电功率/光伏功率场景生成方法
- 9算法刷题题单
- 10机器学习保险行业问答开放数据集: 2. 使用案例_商业保险个性化推荐数据集
(19) 交通预测---基于时空注意力机制的图卷积神经网络
赞
踩
交通预见未来(19): 交通预测---基于时空注意力机制的图卷积神经网络
1、文章信息
《Attention Based Spatial-Temporal Graph Convolutional Networks for Traffc Flow Forecasting》。
北京交通大学博士生校友2019年初发在AAAI顶会上的一篇文章。
2、摘要
针对交通流预测问题,提出了一种基于注意力机制的时空图卷积网络(ASTGCN)模型。ASTGCN主要由三个独立部分组成,分别对交通流的三个时间特性进行建模,即邻近、每日和每周的依赖关系。其中每个独立部分又包含两部分:1)时空注意力机制,有效地捕捉交通数据中的动态时空关联; 2)时空卷积,即同时使用图卷积来捕捉空间模式和常用的标准卷积来描述时间特征。对三个分量的输出进行加权融合,生成最终预测结果。文章应用到加州PeMS的两个数据集上,实验表明所提出的ASTGCN模型性能优于较先进的基准模型。
3、简介
本文提出了一种基于注意力机制的时空图卷积网络(ASTGCN)用于预测交通网络中每个探测器的交通流量。该模型主要贡献总结如下:
(1)提出了一种时空注意机制来研究动态时空相关性。利用空间注意力机制捕捉不同位置之间的动态空间相关性,利用时间注意力机制捕捉不同时间之间的动态时间相关性。
(2)设计了一种时空卷积模块,用于时空相关性建模。它包括从原始的基于图的交通网络结构中获取空间特征的图卷积,以及描述邻近时间依赖关系的标准时间维卷积。
4、主体内容
4.1问题描述和定义
将交通网络定义为无向图G = (V, E, A),如图2(a)所示,其中V为|V | = N个节点的集合;E是一组边,表示节点之间的连通性;A∈R(N×N)表示图G的邻接矩阵。每个节点检测到F个观测值(速度、流量、时间占有率),代表着该节点的 F个特征,如图2(b)实线所示。本文即利用全网过去T个时间节点的数据(速度、流量和时间占有率)预测未来P个时间点的交通流量,即输入为X∈R(N*F*T), 输出为Y∈R(N*P),其中N为观测站数据,F=3为每个节点的三个特征,T为输入的T个时间步,P为输出的时间步。

4.2模型框架

框架主要包含3个部分,本别提取邻近、日、周依赖特征。recent部分包含邻近的T个时段,daily-period 部分包含前一天或多天与预测时段相同的多个时间序列,weekly-period部分前一周或多周与预测时段相同的多个时间序列。该三部分具有相同的网络结构,每部分由多个时空块和一个全连接层组成。在每个时空块中都有时空注意力模块和时空卷积模块。为了优化训练效率,文章采用了残差连接。最后,利用一个参数矩阵对三个分量加权合并,得到最终预测结果。下面对时空注意力模块和时空卷积模块进行详细介绍。

4.3 Spatial-Temporal Attention
(1)空间注意力机制
在空间维度上,不同位置的交通状况相互影响,相互影响具有很强的动态性。因此我们使用注意力机制自适应地捕捉空间维度中节点之间的动态关联性。
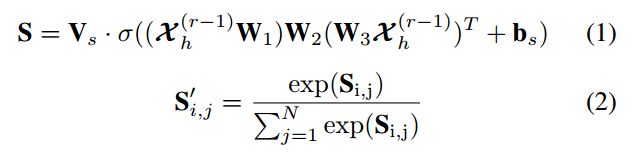
为方便理解,公式(1)简化为:S=V∙σX∙W1∙W2∙W3∙XT+b![]()
维度关系:X∈R(N*C*T),其中N代表N个观测点,C表示channel也即三个观测值(流量,速度和时间占有率),T代表输入的T个时间步。W1∈R(T),W2∈R(T),W3∈R(C*T), V∈R(N*N), b ∈R(N*N), 最终结果S ∈R(N*N)。公式(2)为softmax函数的表示形式,目的是将注意力矩阵S进行归一化。归一化后的注意力矩阵S’在后面的图卷积中将和邻接矩阵A进行相乘。
(2)时间注意力机制
在时间维度上,不同时间段的交通状况之间存在相关性,不同情况下的相关性也不同。同样,我们使用注意机制来自适应地赋予数据不同的权重。
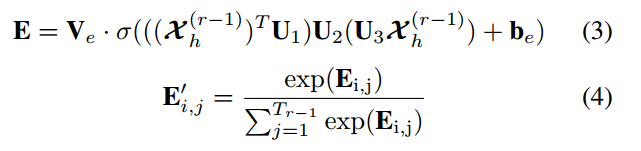
为方便理解,公式(3)简化为: E=V∙σXT∙U1∙U2∙X∙U3+b![]()
维度关系:X∈R(N*C*T),其中N代表N个观测点,C表示channel也即三个观测值(流量,速度和时间占有率),T代表输入的T个时间步。U1∈R(N),U2∈R(C*N),U3∈R(C), V∈R(T*T), b ∈R(T*T), 最终结果E ∈R(T*T)。公式(4)为softmax函数的表示形式,目的是将注意力矩阵E进行归一化。归一化后的注意力矩阵E’将和输入矩阵X进行相乘得到最终输入。

4.4 Spatial-Temporal Convolution
前面的时空注意力模块都是在为图卷积模块准备数据。本文提出的时空卷积模块由空间维上的图卷积和时间维上的标准卷积组成。

(1)空间维度上的图卷积
关于图卷积,目前有两种处理方法,一种是切比雪夫多项式近似:

其中,θ ∈ R(K)为多项式系数的向量,
![]() ,
,
其中λmax为拉普拉斯矩阵的最大特征值,切比雪夫多项式的迭代关系为:
![]()
![]()
公式相当于利用卷积核gθ提取0到(K−1)阶邻居的信息。将空间注意力机制应用到该图卷积过程中即为:
![]()
此外,由于输入数据X∈R(N*C*T),因此对每个时间步要有C个filter。

(注:还有另外一种常用的GCN,即1阶近似,
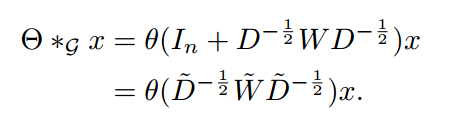 )
)
(2)时间维度上的标准卷积
图卷积获取了邻域信息,在此基础上再叠加标准的卷积层,在时间维度进一步合并相邻的时间步信息, 如图5所示。
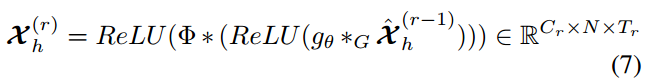
上面介绍的时空注意力模块和时空卷积模块构成了一个总的时空块。多个时空块叠加,可进一步提取更大范围的动态时空关联性。最后,增加一个全连接层,保证各分量的输出具有与预测目标相同的尺寸和维度。最终的全连接层使用ReLU作为激活函数。
4.5特征融合
![]()
5、实验部分
实验部分采用了两个数据集,PeMSD4和PeMSD8。文章代码GitHub 地址:https://github.com/guoshnBJTU/ASTGCN。公众内回复“加州”获取文章数据集下载地址和下载说明。

6、展望
未来可以考虑一些外部影响因素,例如天气因素和大型事件,进一步提高预测精度。
关注微信公众号《当交通遇上机器学习》,
后台回复“数据”即可获取高达175G的四个月的滴滴GPS数据和滴滴订单数据的获取方式,以及从数据处理(Oracle数据库)、模型构建(机器学习)、编程实现(python)到可视化(ArcGIS)等一系列视频教程。
后台回复“纽约”获取美国纽约10年的出租车轨迹数据以及7年的共享单车轨迹数据下载地址。
后台回复“芝加哥”获取美国芝加哥6年的共享单车轨迹数据下载地址。
后台回复“加州”获取美国加州近20年的交通流量监测数据下载地址。
公众号以交通大数据为主线,专注于人工智能、机器学习、深度学习在道路交通和轨道交通领域内的科研前沿与应用,在交通大数据与机器学习的道路上越走越远!



