c语言数据结构——树形结构之树和二叉树_编写一个程序,先用二叉树表示一个简单算术表达式,树的每一个结点包括一个运算符或

前言

二叉树有什么用？
二叉树应用非常广泛。

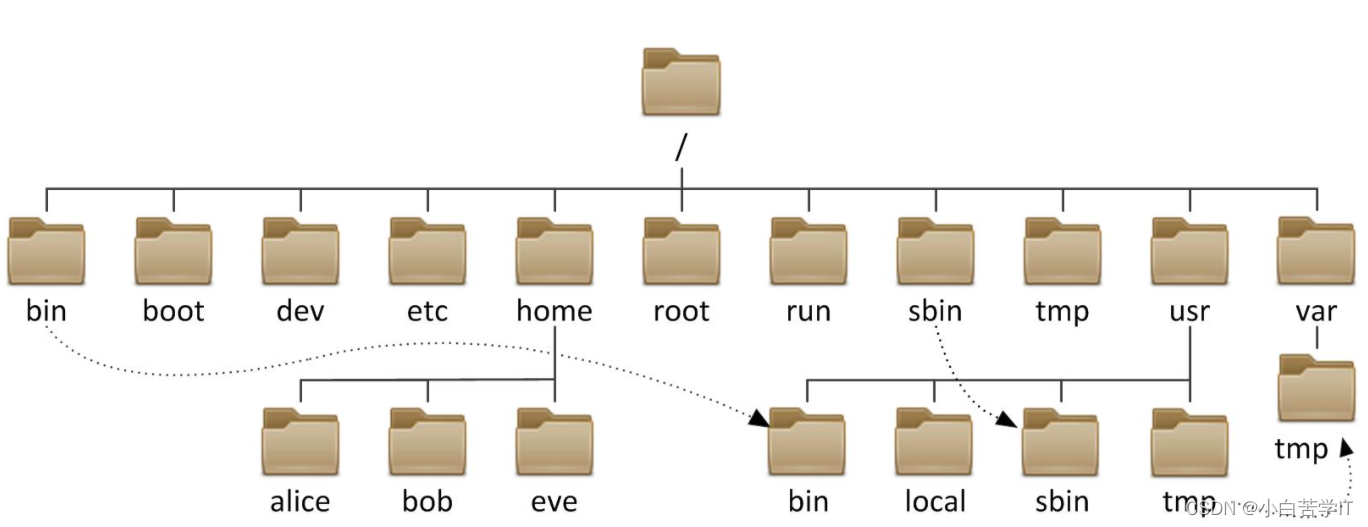
在操作系统源程序中，树和森林被用来构造文件系统。我们看到的window和linux等文件管理系统都是树型结构。在编译系统中，如C编译器源代码中，二叉树的中序遍历形式被用来存放C 语言中的表达式。其次二叉树本身的应用也非常多，如哈夫曼二叉树用于JPEG编解码系统（压缩与解压缩过程）的源代码中，甚至于编写处理器的指令也可以用二叉树构成变长指令系统，另外二叉排序树被用于数据的排序和快速查找。

目录

1.树概念及结构
2.二叉树概念及结构
3.二叉树链式结构的实现

1.树结构及概念（了解）

1.1树的概念

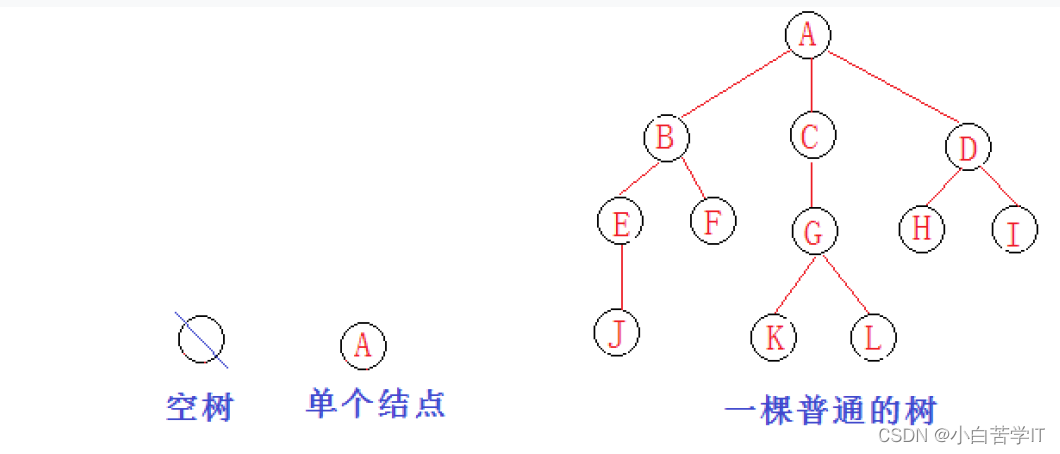
树是一种非线性的数据结构，它是由n（n>=0）个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。
有一个特殊的结点，称为根结点，根节点没有前驱结点
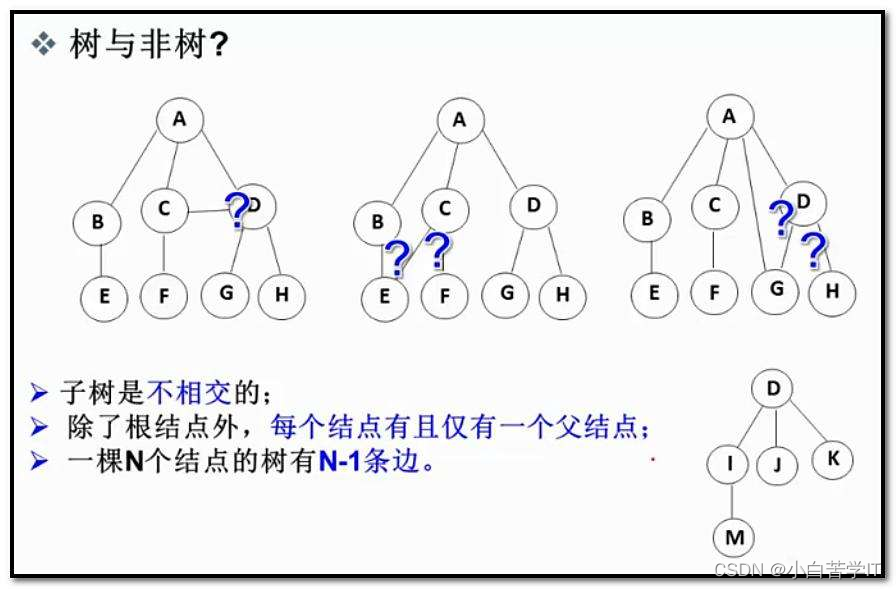
除根节点外，其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm，其中每一个集合Ti(1<= i <= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱，可以有0个或多个后继
因此，树是递归定义的。

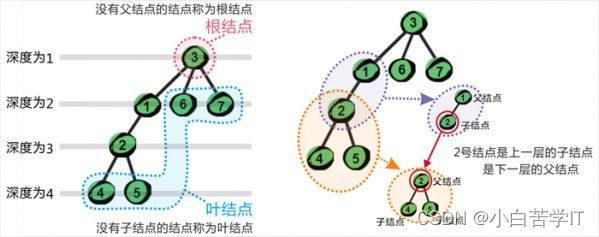
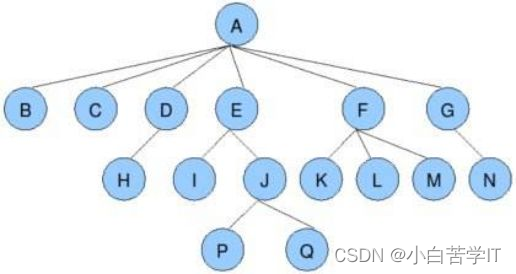
节点的度：一个节点含有的子树的个数称为该节点的度； 如上图：A的为6
叶节点或终端节点：度为0的节点称为叶节点； 如上图：B、C、H、I…等节点为叶节点
非终端节点或分支节点：度不为0的节点； 如上图：D、E、F、G…等节点为分支节点
双亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点； 如上图：A是B的父节点
孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点； 如上图：B是A的孩子节点
兄弟节点：具有相同父节点的节点互称为兄弟节点； 如上图：B、C是兄弟节点
树的度：一棵树中，最大的节点的度称为树的度； 如上图：树的度为6
节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，以此类推；
树的高度或深度：树中节点的最大层次； 如上图：树的高度为4
节点的祖先：从根到该节点所经分支上的所有节点；如上图：A是所有节点的祖先
子孙：以某节点为根的子树中任一节点都称为该节点的子孙。如上图：所有节点都是A的子孙
森林：由m（m>0）棵互不相交的多颗树的集合称为森林；（数据结构中的学习并查集本质就是
一个森林）

1.2树的表示

树结构相对线性表就比较复杂了，要存储表示起来就比较麻烦了，实际中树有很多种表示方式，如：双亲表示法，孩子表示法、孩子兄弟表示法等等。我们这里就简单的了解其中最常用的孩子兄弟表示法。

typedef int DataType;
struct Node
{
  struct Node* _firstChild1;   // 第一个孩子结点
  struct Node* _pNextBrother;  // 指向其下一个兄弟结点
  DataType _data;        // 结点中的数据域
};
1
2
3
4
5
6
7

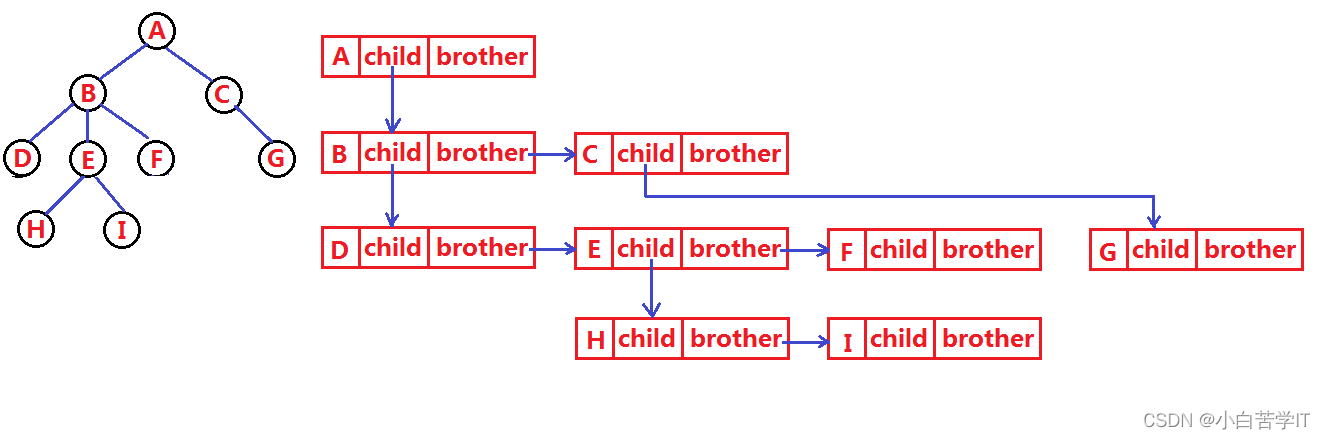
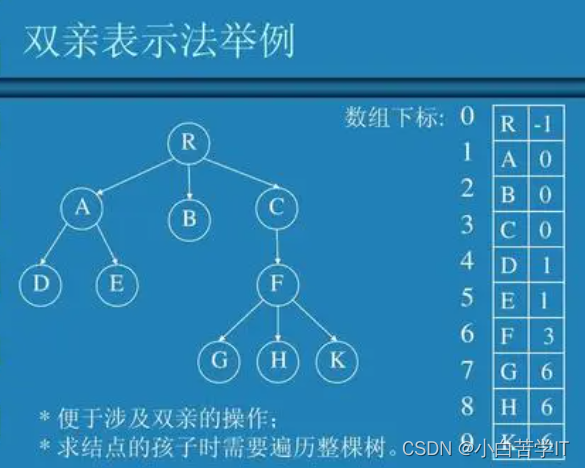
1.3树在实际中的运用（表示文件系统的目录树结构）

2.二叉树概念及结构

2.1概念

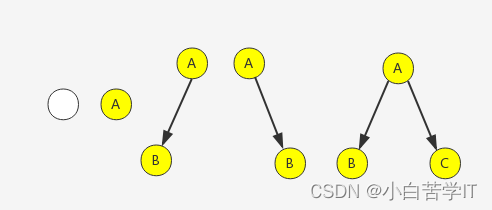
一棵二叉树是结点的一个有限集合，该集合或者为空，或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成。
二叉树的特点：

1. 每个结点最多有两棵子树，即二叉树不存在度大于2的结点。
2. 二叉树的子树有左右之分，其子树的次序不能颠倒。

2.2现实中的二叉树：

2.3数据结构中的二叉树：

2.4特殊的二叉树：

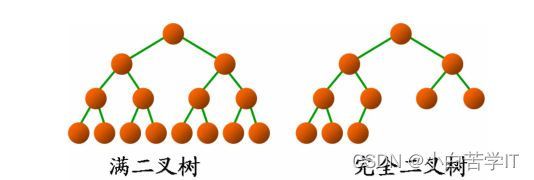
1. 满二叉树：一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。也就是说，如果一个二叉树的层数为K，且结点总数是(2^k) -1 ，则它就是满二叉树。
2. 完全二叉树：完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。

2.5 二叉树的存储结构

二叉树一般可以使用两种结构存储，一种顺序结构，一种链式结构。
二叉树的性质

1. 若规定根节点的层数为1，则一棵非空二叉树的第i层上最多有2^(i-1)个结点.
2. 若规定根节点的层数为1，则深度为h的二叉树的最大结点数是2^h- 1.
3. 对任何一棵二叉树, 如果度为0其叶结点个数为 n0, 度为2的分支结点个数为 n2,则有n0＝n2＋1
4. 若规定根节点的层数为1，具有n个结点的满二叉树的深度，h=LogN

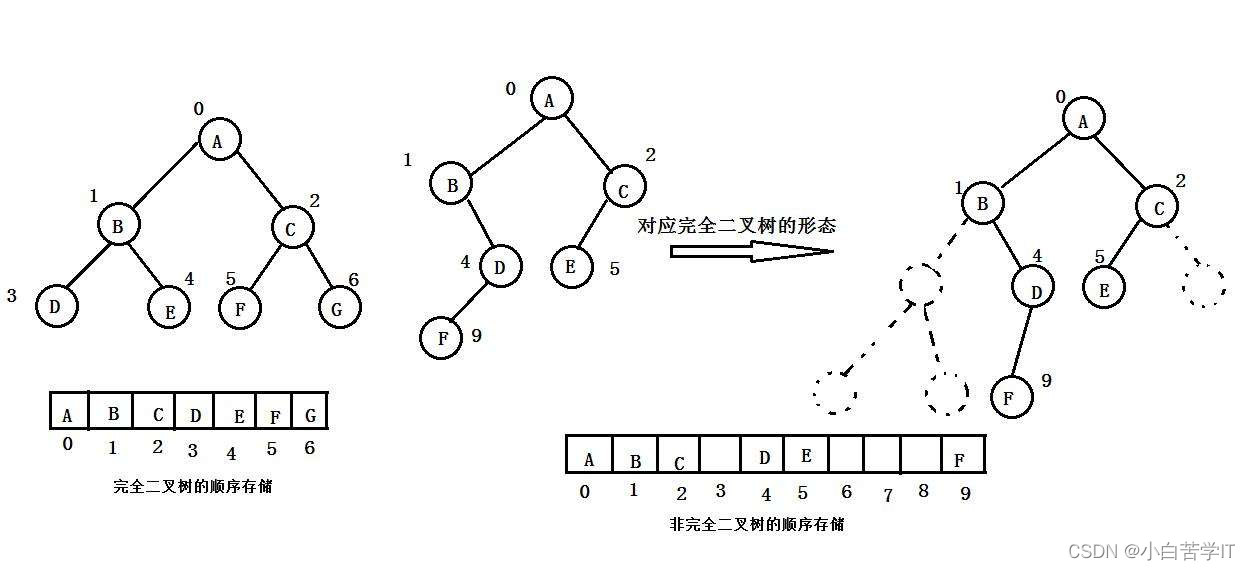
2.5.1 顺序存储：

顺序结构存储就是使用数组来存储，一般使用数组只适合表示完全二叉树，因为不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储。二叉树顺序存储在物理上是一个数组，在逻辑上是一颗二叉树。

2.5.2 链式存储

二叉树的链式存储结构是指，用链表来表示一棵二叉树，即用链来指示元素的逻辑关系。 通常的方法是链表中每个结点由三个域组成，数据域和左右指针域，左右指针分别用来给出该结点左孩
子和右孩子所在的链结点的存储地址 。链式结构又分为二叉链和三叉链，当前我们学习中一般都是二叉链，后面课程学到高阶数据结构如红黑树等会用到三叉链。

下面我们用二叉链表来实现二叉树

//二叉树结构的定义
typedef char BTDataType;

typedef struct BinaryTreeNode
{		
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
	BTDataType data;
}BTNode;

1
2
3
4
5
6
7
8
9
10

先序

//先序
void PrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	printf("%c ", root->data);
	PrevOrder(root->left);
	PrevOrder(root->right);
}
1
2
3
4
5
6
7
8
9
10
11
12

中序

//中序
void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	InOrder(root->left);
	printf("%c ", root->data);
	InOrder(root->right);
}

1
2
3
4
5
6
7
8
9
10
11
12
13

后序

//后序
void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%c ", root->data);
}
1
2
3
4
5
6
7
8
9
10
11
12

求节点个数

//节点个数
int BTNodeSize(BTNode* root)
{
	return root == NULL ? 0 : BTNodeSize(root->left) + BTNodeSize(root->right) + 1;
}
1
2
3
4
5

叶子数

//叶子数
int LeafNodeSize(BTNode* root)
{
	//空节点
	if (root == NULL)
	{
		return 0;
	}
	//叶子节点
	if (root->left == NULL && root->right==NULL)
	{
		return 1;
	}
	//既不是叶子节点也不是空节点

	return LeafNodeSize(root->left) + LeafNodeSize(root->right);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

用队列实现广度优先搜索遍历二叉树

void LevelOrder(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if(root)
	QueuePush(&q, root);

	while (!QueueEmpty(&q))
	{
		BTNode* Front = QueueFront(&q);
		QueuePop(&q);
		printf("%c ", Front -> data);
		if (Front->left)
		{
			QueuePush(&q, Front->left);
		}
		if (Front->right)
		{
			QueuePush(&q, Front->right);
		}

	}
	printf("\n");
	QueueDestroy(&q);

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

Queue.h

#pragma once

#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<stdbool.h>
struct BinaryTreeNode;
typedef struct BinaryTreeNode* QDataType;

typedef struct QueueNode
{
	struct QueueNode* next;
	QDataType data;
}QNode;

typedef struct Queue
{
	QNode* head;
	QNode* tail;
}Queue;

//初始化
void QueueInit(Queue* pq);

//销毁队列
void QueueDestroy(Queue* pq);

//入队列
void QueuePush(Queue* pq, QDataType x);

//出队列
void QueuePop(Queue* pq);

//取队列的队头元素
QDataType QueueFront(Queue* pq);

//取队列的队尾元素
QDataType QueueBack(Queue* pq);

//返回队列长度
int QueueSize(Queue* pq);

//判空
bool QueueEmpty(Queue* pq);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

Queue.c

#define _CRT_SECURE_NO_WARNINGS 1
#include"Queue.h"
//初始化
void QueueInit(Queue* pq)
{
	assert(pq);
	pq->head = NULL;
	pq->tail = NULL;
}

//销毁队列
void QueueDestroy(Queue* pq)
{
	assert(pq);
	QNode* cur = pq->head;
	while (cur)
	{
		QNode* next = cur->next;
		free(cur);
		cur = next;
	}
	pq->head = pq->tail = NULL;

}

//队尾入
void QueuePush(Queue* pq, QDataType x)
{
	assert(pq);
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}
	newnode->data = x;
	newnode->next = NULL;
	if (pq->tail == NULL)
	{
		pq->tail = newnode;
		pq->head = newnode;
	}
	else
	{
		pq->tail->next = newnode;
		pq->tail = newnode;


	}

}

//队头出
void QueuePop(Queue* pq)
{
	//1.一个
	//2.多个
	assert(pq);
	assert(pq->head);
	if (pq->head->next == NULL)
	{
		free(pq->head);
		pq->head = pq->tail = NULL;

	}
	else
	{
		QNode* next = pq->head->next;
		free(pq->head);
		pq->head = next;
	}
}

//取队列的队头元素
QDataType QueueFront(Queue* pq)
{
	assert(pq);
	assert(pq->head);
	return pq->head->data;
}

//取队列的队尾元素
QDataType QueueBack(Queue* pq)
{
	assert(pq);
	assert(pq->head);
	return pq->tail->data;
}

//返回队列长度
int QueueSize(Queue* pq)
{
	assert(pq);
	int size = 0;
	QNode* cur = pq->head;
	while (!cur)
	{
		size++;
		cur = cur->next;
	}
	return size;
}

//判空
bool QueueEmpty(Queue* pq)
{
	assert(pq);
	return pq->head == NULL;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109

test.c

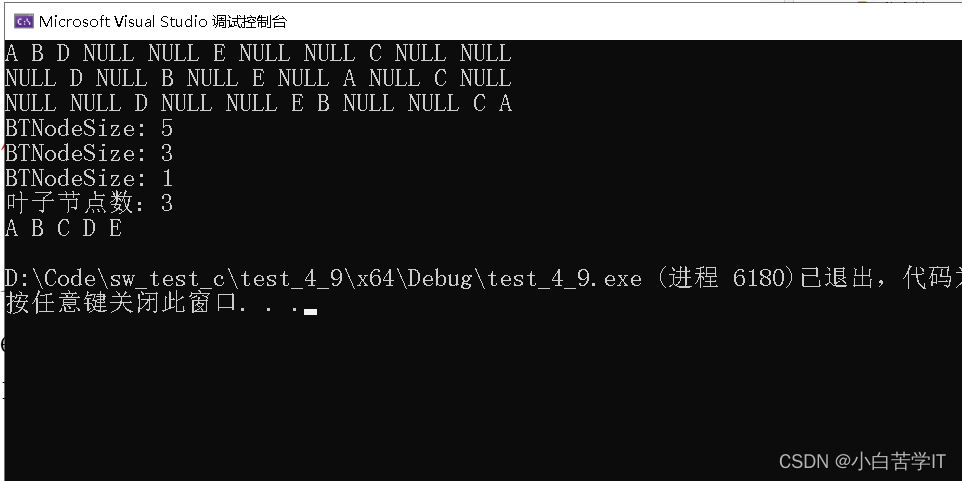
//测试
int main()
{
	BTNode* A =(BTNode*)malloc(sizeof(BTNode));
	A->data = 'A';
	A->left = NULL;
	A->right = NULL;

	BTNode* B=(BTNode*)malloc(sizeof(BTNode));
	B->data = 'B';
	B->left = NULL;
	B->right = NULL;

	

	BTNode* C = (BTNode*)malloc(sizeof(BTNode));
	C->data = 'C';
	C->left = NULL;
	C->right = NULL;


	BTNode* D = (BTNode*)malloc(sizeof(BTNode));
	D->data = 'D';
	D->left = NULL;
	D->right = NULL;
	

	BTNode* E = (BTNode*)malloc(sizeof(BTNode));
	E->data = 'E';
	E->left = NULL;
	E->right = NULL;
	
	A->left = B;
	A->right = C;
	B->right = E;
	B->left = D;


	PrevOrder(A);
	printf("\n");
	InOrder(A);
	printf("\n");
	PostOrder(A);
	printf("\n");
	printf("BTNodeSize: %d\n", BTNodeSize(A));
	printf("BTNodeSize: %d\n", BTNodeSize(B));
	printf("BTNodeSize: %d\n", BTNodeSize(C));
	printf("叶子节点数：%d\n", LeafNodeSize(A));

	LevelOrder(A);
	return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

代码运行结果：