MATLAB（十）方程式求根_matlab求解方程的根

前言

此篇文章是我在B站学习时所做的笔记，主要讲象征性的方法、解决数字根、递归函数，部分为亲自动手演示过的，方便复习用。此篇文章仅供学习参考。

---

提示：以下是本篇文章正文内容，下面案例可供参考

符号寻根法

1. 用符号而不是数字进行数学运算
2. 符号数学是用“符号变量”来完成的
3. 使用sym或syms创建符号变量

>> syms x
>> x + x + x
ans =
3*x
>> (x + x + x)/4
ans =
(3*x)/4

>> y=x^2-2*x-8
y =
x^2 - 2*x - 8
1
2
3
4
5
6
7
8
9
10
11

>> x=sym('x');
>> x + x + x
ans =
3*x
1
2
3
4

符号根查找：solve ()

函数求解可以为方程求根

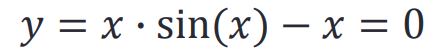
方法一

syms x
y = x*sin(x)-x;
solve(y, x)
ans =
    0
 pi/2
1
2
3
4
5
6

方法二

syms x
solve(x*sin(x)-x, x)
ans =
    0
 pi/2
1
2
3
4
5

>> syms x
>> y=(cos(x))^2-(sin(x))^2;
>> solve(y,x)
ans =
pi/4


>> syms x
y=(cos(x))^2+(sin(x))^2;
solve(y,x)
ans =
Empty sym: 0-by-1
1
2
3
4
5
6
7
8
9
10
11
12

解决多个方程

用符号方法解这个方程：

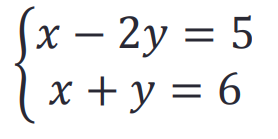
>> syms x y
eq1 = x - 2*y - 5;
eq2 = x + y - 6;
A = solve(eq1,eq2,x,y)
A = 
  包含以下字段的 struct:

    x: [1×1 sym]
    y: [1×1 sym]

>> A.x
ans =
17/3

>> A.y
ans =
1/3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

用符号表示的方程

• 如果给我们一个用符号表示的函数呢?
  

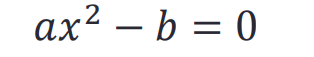
>> syms x a b
>> solve(a*x^2-b)
ans =
  b^(1/2)/a^(1/2)
 -b^(1/2)/a^(1/2)
1
2
3
4
5

• x总是第一个被解决的选项
• 如果想用a和x表示b呢?

>> syms x a b
>> solve(a*x^2-b, b)
ans =
a*x^2
1
2
3
4

Exercise练习

1. 用符号方法求解这个方程
   

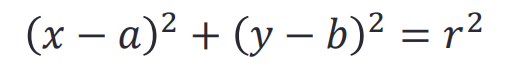
>> syms x a y b r
>> solve((x-a)^2+(y-b)^2-r^2)
ans =
 a + (b + r - y)^(1/2)*(r - b + y)^(1/2)
 a - (b + r - y)^(1/2)*(r - b + y)^(1/2)
1
2
3
4
5

2. 用符号法求矩阵的逆
   

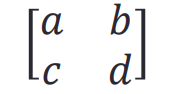
>> syms a b c d 
>> A=[a b;c d]; inv(A)
ans =
[  d/(a*d - b*c), -b/(a*d - b*c)]
[ -c/(a*d - b*c),  a/(a*d - b*c)]
1
2
3
4
5

或

>> syms a b c d 
>> A=[a b;c d];
>> B=inv(A); disp(B)
[  d/(a*d - b*c), -b/(a*d - b*c)]
[ -c/(a*d - b*c),  a/(a*d - b*c)]
1
2
3
4
5

符号区分：diff ()

计算符号函数的导数：

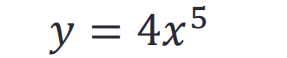
>> syms x
y = 4*x^5; 
yprime = diff(y)
yprime =
20*x^4
1
2
3
4
5

与之前的差值计算区别一下：

>> y=[5 6];
>> diff(y)
ans =
     1
1
2
3
4

Exercise练习

>> syms x 
>> y=(exp(x^2))/(x^3-x+3);
>> yprime=diff(y)
yprime =
(2*x*exp(x^2))/(x^3 - x + 3) - (exp(x^2)*(3*x^2 - 1))/(x^3 - x + 3)^2
1
2
3
4
5

>> syms x y
>> g=((x^2)+x*y-1)/((y^3)+x+3);
>> gprime=diff(g)
gprime =
(2*x + y)/(y^3 + x + 3) - (x^2 + y*x - 1)/(y^3 + x + 3)^2
1
2
3
4
5

象征性的集成：int()

计算符号函数的积分：

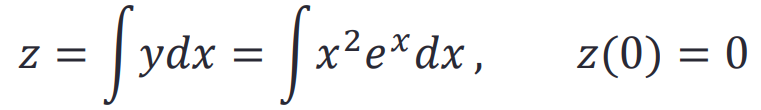
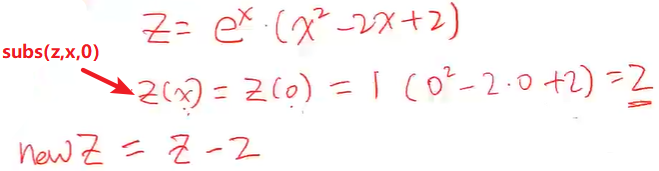
>> syms x; y = x^2*exp(x);
z = int(y); 
>> z
z =
exp(x)*(x^2 - 2*x + 2)

>> z = z-subs(z, x, 0)

z =
exp(x)*(x^2 - 2*x + 2) - 2
1
2
3
4
5
6
7
8
9
10

Exercise练习

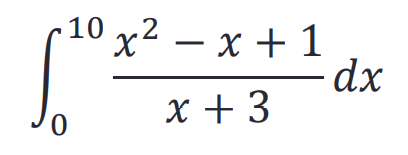
>> y=@(x) (x.^2-x+1)./(x+3); integral(y,0,10)
ans =
   29.0624
1
2
3

回顾函数句柄(@)

• 句柄是指向函数的指针
• 可以用来传递函数给其他函数
• 例如，以下函数的输入是另一个函数：

function [y] = xy_plot(input,x)
% xy_plot receives the handle of a function and plots that 
% function of x
y = input(x); plot(x,y,'r--');
xlabel('x'); ylabel('function(x)');
end
1
2
3
4
5
6

fsolve()

Exercise练习

>> f=@(x) ([2*x(1)-x(2)-exp(-x(1));-x(1)+2*x(2)-exp(-x(2))]);
>> fsolve(f,[-5 -5])

Equation solved.

fsolve completed because the vector of function values is near zero
as measured by the value of the function tolerance, and
the problem appears regular as measured by the gradient.

<stopping criteria details>

ans =

    0.5671    0.5671
1
2
3
4
5
6
7
8
9
10
11
12
13
14

fzero()

当且仅当函数穿过x轴时，求零

>> f=@(x)x.^2
fzero(f,0.1)

f =

  包含以下值的 function_handle:

    @(x)x.^2

正在退出 fzero: 将终止搜索包含符号变化的区间
 因为在搜索期间遇到 NaN 或 Inf 函数值。
(-1.37296e+154 处的函数值为 Inf。)
请检查函数或使用其他起始值重试。

ans =

   NaN

>> fsolve(f,0)

Equation solved at initial point.

fsolve completed because the vector of function values at the initial point
is near zero as measured by the value of the function tolerance, and
the problem appears regular as measured by the gradient.

<stopping criteria details>

ans =

     0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

求多项式的根：roots()

求这个多项式的根：

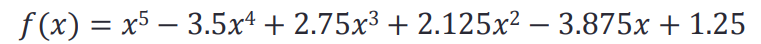
>> roots([1 -3.5 2.75 2.125 -3.875 1.25])

ans =

   2.0000 + 0.0000i
  -1.0000 + 0.0000i
   1.0000 + 0.5000i
   1.0000 - 0.5000i
   0.5000 + 0.0000i
1
2
3
4
5
6
7
8
9

二分法(或分组法、方括号法)

二分算法流程图

牛顿迭代法(打开)

牛顿迭代算法流程图

递归函数

• 调用自身的函数
• 例如，整数n的阶乘
  
• 一个阶乘可以用另一个阶乘来定义：
  
  
  

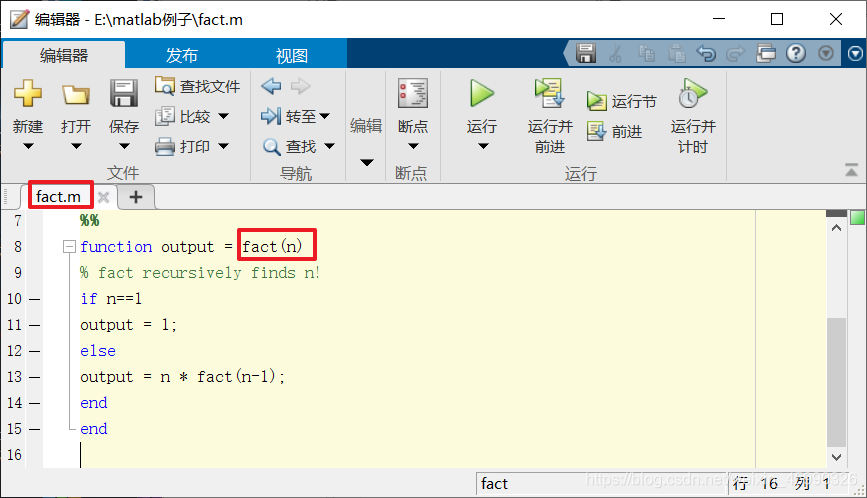
>> fact(3)

ans =

     6
1
2
3
4
5

---

如若侵权，请及时与我联系。