瑞利 随机 matlab,matlab产生瑞利分布随机信号

2.6 (1) 产生均匀分布的随机数x~U (0,1);

(2) 产生服从2σ=4的瑞利分布的随机数y ；

分析：y 的分布函数：82

1)(y Y e y F --= 其反函数为)1ln(8)(1x x F Y --=- 令)1ln(8)(1x x F y Y --=

=-，此处有x~U (0,1) 则y 是满足2σ=4的瑞利分布的随机数

(3) 利用直方图确定PDF ；

分析：首先，利用hist 指令统计落入每个区间的次数，记作N ；然后将其除以总的随

机数数目得到概率；最后除以区间长度得到PDF 估计。

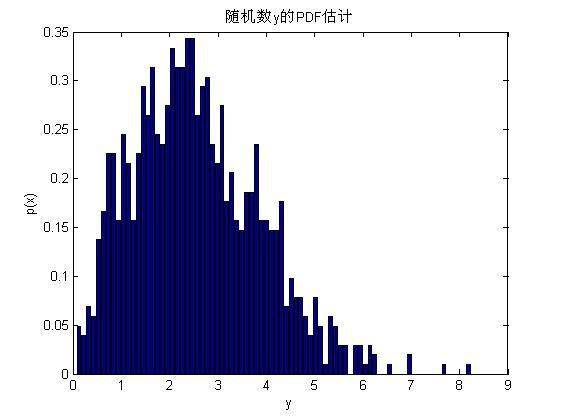
(4) 绘制y 的PDF 直方图；

MATLAB 代码：

>> x=rand(1,1000); % 产生随机数x~U (0,1)

>> y=sqrt(-8.*log(1-x)); % 产生服从2

σ=4的瑞利分布的随机数y

>> M=80; % 设置划分y 值的统计区间数目

>> [N,Y]=hist(y,M); % 统计落入每个区间的次数赋值给N ，区间坐标赋值给Y >> N=N/1000/((max(y)-min(y))/M); % 由统计的区间内次数求PDF

>> bar(Y,N); % 绘制PDF 直方图

>> title('随机数y 的PDF 估计');

>> ylabel('p(x)');

>> xlabel('y');

结果：