Cpp五条

这个屌丝很懒，什么也没留下！

热门标签

基于MATLAB的三维数据插值拟合与三次样条拟合算法（附完整代码）_matlab三维插值

作者：Cpp五条 | 2024-02-16 22:03:40

踩

matlab三维插值

一. 三维插值

首先三维网格生成是利用meshgrid()函数，在MATLAB中调用格式如下：


[x,y,z]=meshgrid(x1,y1,z1)
% x1,y1,z1为这三维数据所需要的分割形式，均以向量形式给出
%返回的x,y,z为网格的数据生成，也是三维数组

三维插值运算，主要利用griddata()函数与interp()函数，如下：


griddata3()  %三维非网格形式的插值拟合
griddatan()  %n维非网格形式的插值拟合
interpn()    %N维网格数据的插值拟合

实际上，interp3()和interpn()调用格式与interp2()函数一致；

griddata3()和griddatan()调用格式与griddata()函数一致。

有关interp2()与griddata()函数可见之前的博客：

基于MATLAB的二维与三维插值拟合运算（附完整代码）_唠嗑！的博客-CSDN博客

基于MATLAB的数据插值运算：Lagrange与Hermite算法（附完整代码）_唠嗑！的博客-CSDN博客

例题1

通过函数V(x,y,z)来生成一些网格型样本点，试根据样本点进行拟合，并给出拟合误差。

$V(x,y,z)=e^{x^2z+y^2x+z^2y}cos(x^2yz+z^2yx)$

解：

MATLAB代码如下：


clc;clear;
 
[x,y,z]=meshgrid(-1:0.2:1);
[x0,y0,z0]=meshgrid(-1:0.05:1);
V=exp(x.^2.*z+y.^2.*x+z.^2.*y).*cos(x.^2.*y.*z+z.^2.*y.*x);
V0=exp(x0.^2.*z0+y0.^2.*x0+z0.^2.*y0).*cos(x0.^2.*y0.*z0+z0.^2.*y0.*x0);
 
V1=interp3(x,y,z,V,x0,y0,z0,'spline');
err=V1-V0;
max(err(:))

运行结果：

ans =0.041862381154469

二. 高维度插值拟合

interpn()函数可实现一维、二维、三维和N维网格数据的插值。常用的有五种格式：

格式一

Vq=interpn(X1,X2,...,Xn,V,Xq1,Xq2,...,Xqn)

格式二

Vq=interpn(V,Xq1,Xq2,...,Xqn)

格式三

Vq=interpn(V)

样本值之间间隔分割一次

格式四

Vq=interpn(V,k)

将每个维度上样本值之间的间隔反复分割k次，形成优化网格，并在这些网格上返回插入值。这将在样本值之间生成 $2^k-1$ 个插入点

格式五

Vq=interpn(_,method,extrapval)

可以指定备选插值方法，包含：'linear','nearest','pchip','cubic','makima'或者'spline'。默认方法为'linear'。

例题2

自行选取数据，利用interpn()函数进行一维插值，二维插值与三维差值。

解：

（1）一维插值

MATLAB代码如下：


clc;clear;
x=[1 2 3 4 5];
v=[12 16 31 10 6];
xq=(1:0.1:5);
vq=interpn(x,v,xq,'cubic');
plot(x,v,'o',xq,vq,'-');
legend('Samples','Cubic Interpolation');

运行结果：

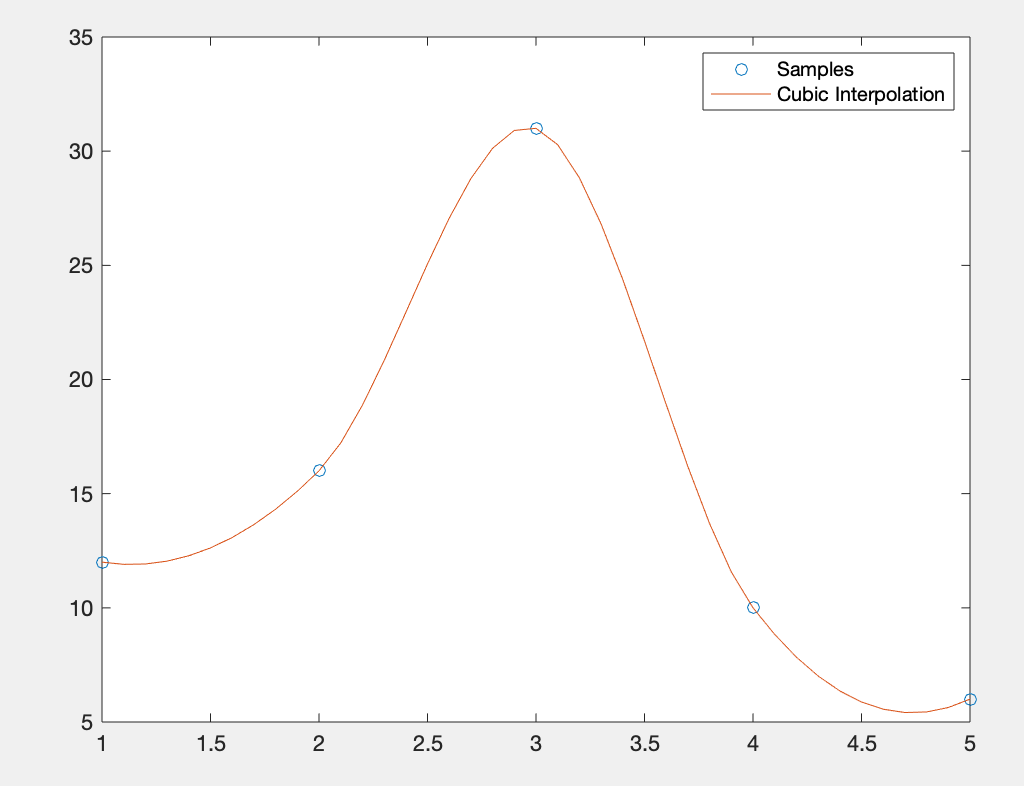
（2）二维插值

MATLAB代码如下：


clc;clear;
[X1,X2]=ndgrid(-5:1:5);
R=sqrt(X1.^2+X2.^2)+eps;
V=sin(R)./(R);
Vq=interpn(V,'cubic');
mesh(Vq);
size(V);
size(Vq);

运行结果：

（3）三维插值

此例子将给定函数 $z=f(x,y)=(x^2-2x)e^{-x^2-y^2-xy}$

MATLAB代码如下：


clc;clear;
[x,y]=ndgrid(-3:.6:3,-2:.4:2);
z=(x.^2-2*x).*exp(-x.^2-y.^2-x.*y);
[x1,y1]=ndgrid(-3:.2:3,-2:.2:2);
z1=interpn(x,y,z,x1,y1);
surf(x1,y1,z1),axis([-3,3,-2,2,-0.7,1.5])

运行结果：

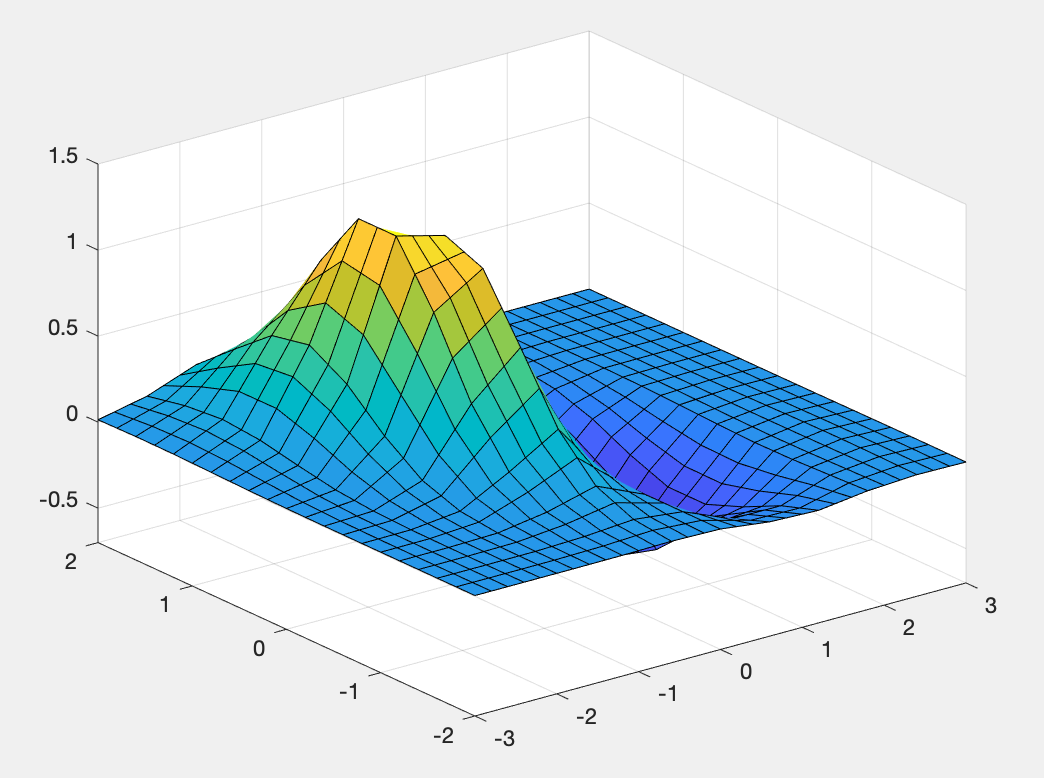
三. 单变量三次样条插值

给定样本点，平面上n个点 $(x_i,y_i)(i=1,2,\cdots,n)$ ，且满足 $x_1<x_2<\cdots<x_n$ 。

S(x)为三次样条函数需要满足如下三个条件：

$S(x_i)=y_i(i=1,2,\cdots,n)$ ，即函数经过样本点
S(x)在每个子区间 $[x_i,x_{i+1}]$ 上为三次多项式，即 $S(x)=c_{i1}(x-x_i)^3+c_{i2}(x-x_i)^2+c_{i3}(x-x_i)+c_{i4}$
S(x)在整个区间 $[x_1,x_n]$ 上有连续的一阶以及二阶导数

在MATLAB中，定义一个三次样条函数类，如下：

S=csapi(x,y)

上式子中 $x=[x_1,x_2,\cdots,x_n],y=[y_1,y_2,\cdots,y_n]$ 为样本点。S返回样条函数对象的插值结果，其中就包含子区间点，各区间点三次多项式系数等等。

可以利用fnplt()绘制出插值结果，调用格式如下：

fnplt(S)

对给定的向量xp,可用fnval()函数进行计算，调用格式如下：

yp=fnval(S,xp)

由此式子得出的yp是xp上各点的插值结果。

例题3

以sin(x)产生的数据点为例子，进行三次样条插值运算。

解：

MATLAB代码如下：


clc;clear;
x0=[0,0.4,1,2,pi];
y0=sin(x0);
sp=csapi(x0,y0),fnplt(sp,':');
hold on,ezplot('sin(t)',[0,pi]);
plot(x0,y0,'o')
sp.coefs

运行结果：

sp =

包含以下字段的 struct:

form: 'pp'
breaks: [0 0.400000000000000 1 2 3.141592653589793]
coefs: [4×4 double]
pieces: 4
order: 4
dim: 1

ans =

-0.162650313526554 0.007585653997624 0.996535644336825 0
-0.162650313526551 -0.187594722234240 0.924532017042179 0.389418342308651
0.024435716847400 -0.480365286582031 0.523756011752416 0.841470984807897
0.024435716847400 -0.407058136039832 -0.363667410869446 0.909297426825682

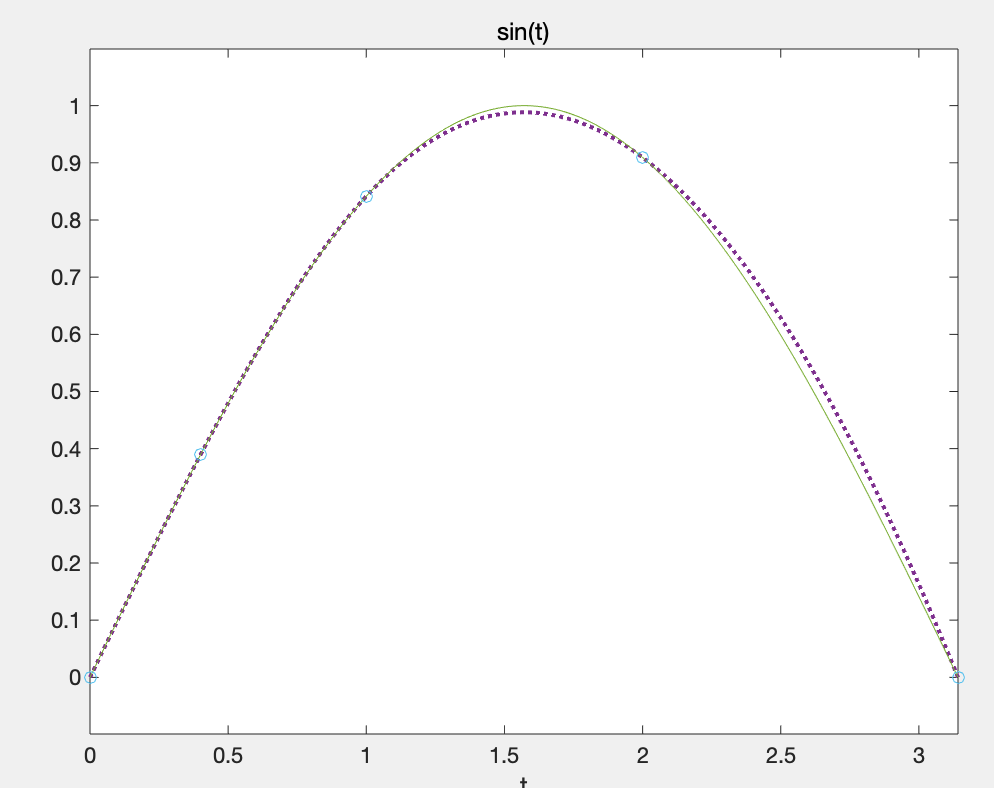
根据运算的结果，在(0.4000,1)区间内，插值多项式可以表示为如下：

$S_2(x)=-0.1627(x-0.4)^3-0.1876(x-0.4)^2+0.9245(x-0.4)+0.3894$

例题4

自行选取函数f(x)的一些数据点，用三次样条插值的方法对这些数据进行拟合。

$f(x)=(x^2-3x+5)e^{-5x}sinx$

解：

MATLAB代码如下：


clc;clear;
x=0:.12:1;
y=(x.^2-3*x+5).*exp(-5*x).*sin(x);
sp=csapi(x,y);
fnplt(sp)
c=[sp.breaks(1:4)' sp.breaks(2:5)' sp.coefs(1:4,:),sp.breaks(5:8)'...
    sp.breaks(6:9)' sp.coefs(5:8,:)]

运行结果：

c =

列 1 至 7

0 0.120000000000000 24.739556929256214 -19.358812904771273 4.515070686988533 0 0.480000000000000
0.120000000000000 0.240000000000000 24.739556929256135 -10.452572410239041 0.937704449187296 0.305791530983672 0.600000000000000
0.240000000000000 0.360000000000000 4.507107987633279 -1.546331915706831 -0.502164069926209 0.310548976552460 0.720000000000000
0.360000000000000 0.480000000000000 1.913943736028591 0.076226959841147 -0.678576664630090 0.235810391177767 0.840000000000000

列 8 至 12

0.600000000000000 -0.240386219157313 0.765246704811441 -0.577599824871780 0.158786154419726
0.720000000000000 -0.477388221775507 0.678707665914812 -0.404325300384630 0.100078340597694
0.840000000000000 -0.455907214289051 0.506847906075627 -0.262058631745777 0.060507768093483
0.960000000000000 -0.455907214289066 0.342721308931568 -0.160110325944914 0.035571534465187

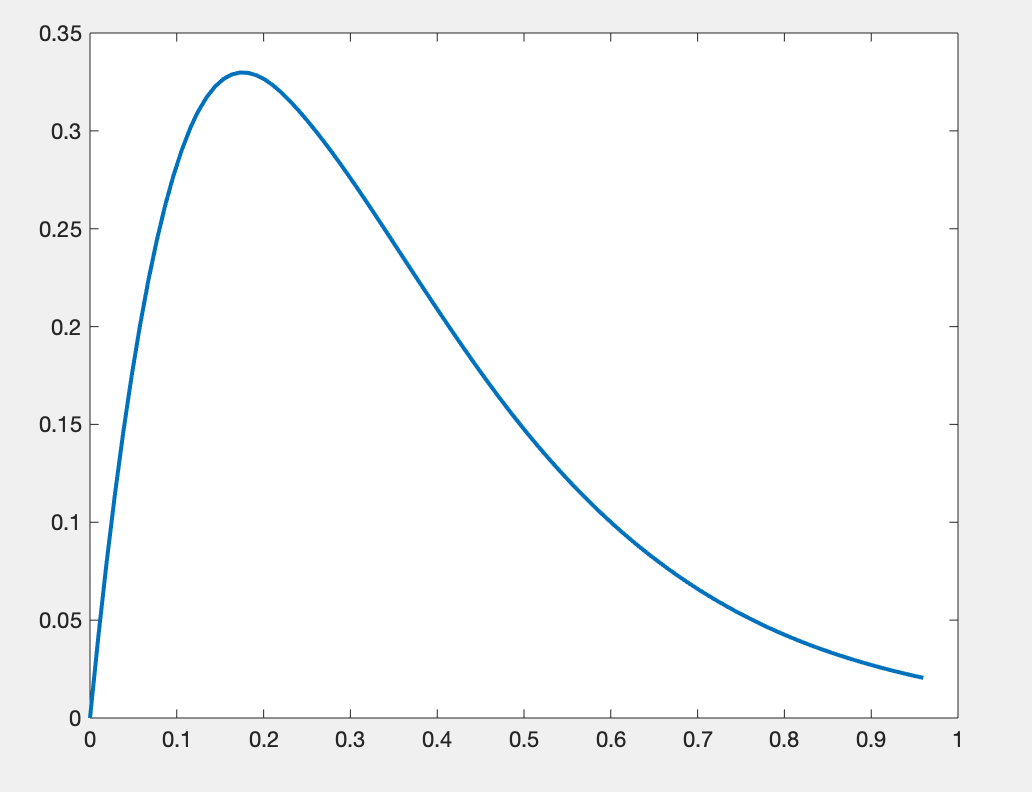
四. 多变量三次样条插值

处理多个自变量的网格数据三次样条插值的格式如下：


S=csapi({x1,x2,...,xn},z)
%xi为自变量的网格标志
%z是网格数据的样本点
%得到的S是三次样条函数对象

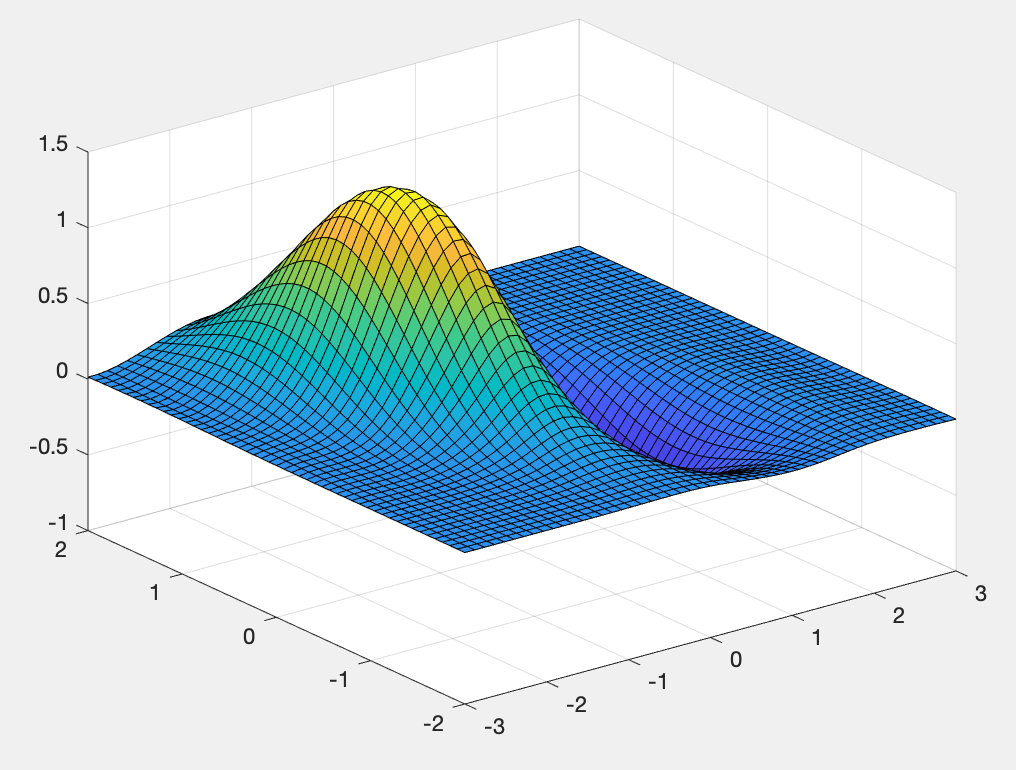
例题5

用三次样条插值方法得出z函数网格数据的样条插值拟合，并绘制出曲面

$z=f(x,y)=(x^2-2x)e^{-x^2-y^2-xy}$

解：

MATLAB代码如下：


clc;clear;
 
x0=-3:.6:3;
y0=-2:.4:2;
[x,y]=ndgrid(x0,y0);
%注意此处只能使用ndgrid，否则生成的z矩阵的顺序有问题
 
z=(x.^2-2*x).*exp(-x.^2-y.^2-x.*y);
sp=csapi({x0,y0},z);
fnplt(sp);

运行结果：

在MATLAB中，函数spline也可以进行三次样条数据插值，格式如下：

yy=spline(x,y,xx)

例题6

对离散分布在y函数曲线上的数据点进行样条插值计算。

$y=e^xsinx$

解：

MATLAB代码如下：


clc;clear;
 
x=[0 2 4 5 8 12 12.8 17.2 19.9 20];
y=exp(x).*sin(x);
xx=0:.25:20;
yy=spline(x,y,xx);
plot(x,y,'o',xx,yy)

运行结果：

声明：本文内容由网友自发贡献，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：【wpsshop博客】