On Characterizing GAN Convergence Through Proximal Duality Gap翻译_模型近端平衡

通过近端二偶间隙表征GAN收敛

Abstract

尽管生成对抗网络(GANs)在建模数据分布方面取得了成就，但训练它们仍然是一项具有挑战性的任务。造成这一困难的一个因素是GAN损失曲线的非直观性质，这需要对生成的输出进行主观评估来推断训练进度。近年来，在博弈论的激励下，对偶差距被提出作为一种监测GAN训练。然而，它仅限于当GAN收敛于纳什均衡（Nash equilibrium）时的设置。但是GANs并不需要总是收敛于纳什均衡来模拟数据分布。在这项工作中，我们将对偶间隙的概念扩展到近端对偶间隙（proximal duality gap），这适用于纳什均衡可能不存在的训练GAN的一般背景。我们从理论上证明了近端对偶性间隙能够监测GANs到包含纳什均衡的更广泛的均衡谱（spectrum of equilibria）的收敛性。我们还在理论上建立了不同GAN公式的近端对偶性间隙与真实数据分布和生成的数据分布之间的散度之间的关系。我们的研究结果为GAN收敛的本质提供了新的见解。最后，我们通过实验验证了近端对偶性间隙在监测和影响GAN训练方面的有效性。

1. Introduction

生成性建模(Generative modeling)是一种重要的机器学习范式，旨在学习数据分布。从给定的经验分布中参数化建模真实世界数据的真实底层分布的能力，带来了产生新的和看不见的实例的能力。生成对抗网络可能是最流行和最成功的学习数据分布的创新。GAN将生成建模问题表述为两个代理——鉴别器(D)和生成器(G)之间的零和博弈（zero-sum game）。该鉴别器旨在区分生成器产生的假样本和属于真实数据分布的样本。另一方面，生成器试图通过学习从输入噪声空间到数据空间的映射来欺骗鉴别器。生成器也可以看作是对鉴别器进行对抗性攻击，利用通过鉴别器的信息泄漏，在游戏进入平衡时学习真实数据分布。
在正式意义上，GAN游戏被定义为：

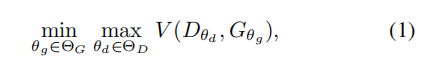
其中生成器(由θg参数化)和鉴别器(由θd参数化)是神经网络，V是代理寻求优化的目标函数。不同的GAN公式产生V的不同表达式，每个表达式都最小化真实数据分布和生成的数据分布之间的唯一差异。 经典的GAN公式(Goodfelletal.，2014)将JS最小化散度，定义为

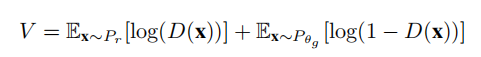
其中，Pr表示真实的数据分布，Pθg表示生成的数据分布。

在任何学习问题中，损失函数的轨迹都应该表明训练模型的优度。然而，这种直观的推论不能从GAN的损失曲线中得出。这是因为GAN的经典训练涉及到目标函数w.r.t即个体代理的交替梯度下降优化。代理的每个优化步骤都会改变其对手的损失表面，导致随着时间的推移，这两个代理的非直观的损失曲线。图1显示了当GAN(a)收敛和(b)发散时的鉴别器和发生器损失曲线。理想情况下，损失应在模型收敛时减少，而在发散时增加。然而，当我们观察到当GAN收敛时，生成器损耗减少，鉴别器损耗增加。当它发散时，这两种损失之间就存在着相互作用。

而这些损失曲线则没有深入了解GAN性能的逐渐改进或退化。因此，监控GANs通常需要对生成的输出进行主观评估。因此，对架构和超参数空间进行穷尽搜索以找到GAN博弈所需的微妙平衡是不可行的。这增加了GAN训练的复杂性，由于最小-最大梯度优化造成的不稳定性，这已经具有挑战性了。能够量化GAN培训进度的客观措施可以降低训练的复杂性。

对偶性差距(DG)(Grnarava等人，2019)，基于博弈论原则，是最近提出的监测GAN训练的客观措施。DG根据代理偏离GAN配置以寻找更好的最优值的能力来量化GAN配置的优点。当一个GAN收敛到纳什均衡时，没有一个代理可以单方面偏离以找到更好的最优值，因此DG将为零。量化收敛性的能力以及领域不可知的性质，既不需要预先训练的模型，也不需要标记的数据，使DG成为监测GAN训练的一个潜在的强大工具。

然而，DG依赖于gan收敛于纳什均衡的概念。相反，最近的研究(Farnia&Ozdaglar，2020；Berard等人，2020)表明，对于GAN并不总是存在纳什均衡，特别是在大多数现代GAN公式使用的正则化环境下进行训练时。GANs可以收敛到非纳什均衡的稳定平稳点，同时产生具有高保真度的真实数据样本。这削弱了建立DG作为GANs性能监控工具的概念的基础，引发了以下问题：即使在非纳什临界点，gans也能捕获真实的数据分布吗？如果是这样，在这些静止点上的DG会是零吗？如果没有，我们如何在这种情况下监控GAN培训？

在本研究中，我们通过介绍gan的近端对偶性间隙的概念可推广到纳什均衡可能不存在的情况来研究上述问题。我们的工作是基于GAN的近端平衡的概念，它作为描述GAN最优性的一般概念(Farnia&Ozdaglar，2020)。我们根据代理优化近端GAN目标的能力来定义DG(见Eq。9)，并称之为近端二元性间隙(DG^λ)。GAN对策的近端平衡态(式。1)是一个关于近端目标的纳什均衡。因此，当GAN博弈达到近端平衡时，DG^λ将趋于零，表明模型的收敛性。由于所有纳什均衡都形成了近端均衡的子集，DG^λ作为一种通用的稳健度量，可以量化野外的GAN收敛。

总的来说，我们做出了以下贡献：

• 我们提出了DG对监测GAN训练的严重局限性。
• 我们提出了一个理论上有基础的和鲁棒的扩展-DG^λ，它克服了这一限制，也适用于更广泛的背景下，当GANs收敛于一个非纳什均衡时。
• 利用DG^λ，我们推导了GAN收敛的本质。具体地说，我们研究了学习数据分布的质量与博弈平衡之间的关系。我们证明，对于各种GAN，一个构型(θd，θg)，其中P_θg=P_r对应于一个斯塔克尔伯格平衡（Stackelberg equilibrium）。
• 我们通过实验证明了DG^λ在监测和影响GAN训练方面的熟练程度

2. Related Work

由于GAN损失曲线的不可推断性，开发监测GAN训练的外部措施已成为一个活跃的研究领域（Borji，2019；Lucic等人，2018；Olsson等人，2018）。现有的测量方法，如平均对数似然(Goodfell等人，2014；Theis等人，2016)、感觉评分(IS)(Salimans等人，2016)、弗雷切特感觉距离(FID)(Heusel等人，2017) 评估GANs的输出，但需要预先训练的模型 。此外，这些措施，包括最近的措施，如精度和召回率(Sajjadi等人，2018；KynK¨a¨¨等人，2019)、密度和覆盖率(托尔斯蒂欣等人，2017；Naeem等人，2020)不监测训练进展，也不描述GAN游戏的平衡。

对偶差距(DG) 是最近提出的一个领域不可知和计算可行的度量，用于监测和评估GAN训练。当GAN收敛到纳什均衡时，DG为零，使其成为客观监测GAN训练的一个有吸引力的度量
然而，由于梯度的消失，DG的估计过程有一个根本的局限性。在估计对偶间隙（扰动的对偶间隙）之前，向GAN配置添加扰动有助于克服这个问题(Sidheekhetal.，2020)。但这两种方法都假设GANs收敛到纳什均衡，这可能并不总是如此，特别是对于高维数据集（正如我们在下一节中演示的）。因此，限制了DG和干扰DG对监测GAN培训的适用性

3. Background

3.1. A Brief Overview of GAN formulations

Classic GAN
经典GAN(Goodfelletal.，2014)公式的最小最大目标是：

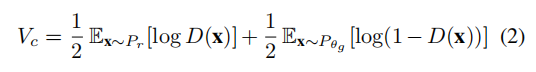
其中，概率鉴别器D输出输入数据点属于真实数据分布的可能性。鉴别器的目标是最大化学习条件概率P(y|x)的对数似然，其中y=0和1分别表示假数据点和真实数据点。将上述目标关于，最优鉴别器的生成器最小化 相当于最小化P_θg和P_r之间的简森·香农散度(JSD)（Jenson Shannon divergence）。

F-GAN
F-GAN(Nowozin等人，etal.，2016)是经典GAN的推广，通过合并变分散度估计框架的扩展来最小化任意f−发散(Nguyenet等人，2010)。对于满足f（1）=0的凸下半连续函数f：R+→R，分布P和Q之间的f−散度为，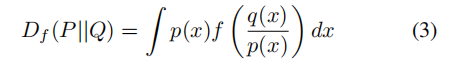
F-GAN目标 即 P_θg和P_r之间最小化f−散度(Df) 的定义为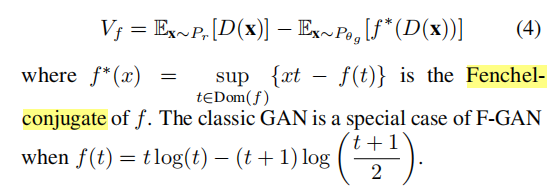
Wasserstein GAN (WGAN):
WGAN将GAN博弈定义为P_θg和P_r之间的最优传输成本，即沃瑟斯坦距离（Wasserstein distance），这是一个更有效的成本函数来学习支持低维流形的数据分布(Arjovskyetal.，2017)。特别地，Kantorovich-Rubinstein duality被用来达到Wasserstein-1 (Earth Movers) distance between the distributions defined as: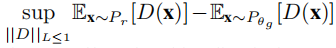
其中上确界控制在所有 1-Lipschitz 鉴别器身上。在实践中，Lipschitz约束是通过剪权（weight clipping）来实现的，从而实现以下WGAN目标：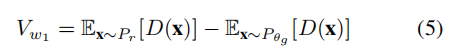
WGAN公式还将扩展到一般运输成本（general transport cost）(Farnia&Tse，2018) c(x，y)，通过限制鉴别器为 c-concave as
尽管Wasserstein distance比其他差异（divergences）稳定，训练GAN仍然是一项艰巨的任务。这促使人们努力理解GAN收敛的本质。

3.2. Understanding GAN convergence

GAN平衡的经典概念
传统上，GAN博弈被期望收敛到一个纯纳什均衡，这种配置(θ_d^∗，θ_g^∗)是最优的。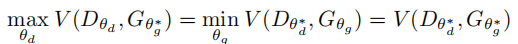
具有无限容量的GAN在这样的解决方案下学习真实的数据分布(Goodfelletal.，2014)。然而，对于零和博弈，纯纳什均衡并不总是存在的(Nash，1950)。只有一个扩展的概念，混合策略纳什均衡(MNE)被保证存在。最近的GAN公式明确地寻求MNE(Arora等人，2017；Hsieh等人，2019)。由于混合策略给出了模型参数的分布，GAN收敛的平稳点对于双方来说都不必是单独最优的。

GANs Need Not Converge to Nash Equilibria
利用稳定性的概念从优化角度研究了GAN收敛（达斯卡拉基斯等，2018；菲伊兹等，2019；纽埃等，2019；张等，2019b；马祖达等，2019；莫赫塔里等，2020；林等，2020）。由于GAN公式是非凸的，因此在采用基于梯度的优化时，只能得到局部平衡的替代.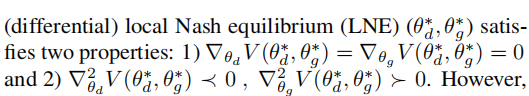
然而最近的文献表明存在许多非LNE的替代梯度下降优化，也没有产生真实的数据，并提出了逃避这些吸引子的方法。(Fiez等人，2019；Jin等人，2020)研究了顺序博弈的梯度动力学，建立了它们唯一稳定的稳定吸引子是Stackelberg equilibria。然而，学习到的数据分布与游戏配置之间的关系尚未得到很好的研究。此外，最近的实证研究(Berard等人，2020；Farnia&Ozdaglar，2020)也表明，GANs不需要获得LNE来产生真实的数据。

我们通过在CIFAR-10数据集上训练光谱归一化GAN(SNGAN)100个epoch，确保模型收敛产生高保真样本。由于局部纳什均衡对于代理是局部最优的，优化目标函数 w.r.t（关于）任何个人玩家 （optimizing the objective function w.r.t any individual player）都不应该促进玩家离开这样一个点。然而，如图2所示，在进一步 优化目标函数只w.r.t生成器（optimizing the objective function w.r.t only the generator.）时， 生成器偏离了所达到的平衡。虽然生成器获得较低的成本，但产生的样品的质量明显恶化。这意味着GAN并没有收敛到一个LNE。 ，我们通过验证生成器参数的目标w.r.t的顶k特征值(λ_K)（按大小计算）（verifying the top-K
eigenvalues (λK) (by magnitude) of the Hessian of the objective w.r.t the generator’s parameters），进一步加强了这一主张。然而，如图2所示，Hessian同时具有正特征值和负特征值，违反了LNE的第二个特性，从而强调GANs可以收敛到非纳什吸引子（ non-Nash attractors），同时产生高保真样本。在补充材料中讨论了为MNIST和celeb-a数据集训练的GANs的类似结果。

Proximal Equilibria（近端平衡） for GANs
大多数试图表征GANs平衡的研究假设模型的无限容量（可实现的设置）。然而，在实践中，大多数GAN架构采用 标准化 和 正则化 来实现最先进的性能。最近的一项研究(Farnia&Ozdaglar，2020)对在不可实现环境下的GAN收敛提出了一个平衡的更一般的概念——近端平衡(PE)。平衡的概念是从GAN的顺序博弈角度，在温和的连续性假设下保证存在Stackelberg平衡。Farnia和Ozdaglar在原始GAN目标上定义了一个近端算子，允许鉴别器在附近是最优的（由λ控制），

4. Proximal Duality Gap

我们首先定义GANs的经典对偶间隙，然后转向提出的度量。

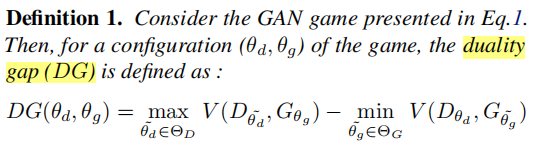
在纯Nash equilibrium(θd∗，θg∗)下，

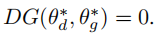
DG有一些有趣的特性。
首先，下界为P_r和P_θg之间的JSD(V=Vc)。
其次，由于DG适用于任何GAN目标V(D，G)，并且不需要预先训练的分类器或标记数据，因此它是领域不可知的，与其他普遍的评估措施相比，它可能能够更好地监测GAN训练。然而，如前所述，GANs可以收敛到非纳什吸引子，其中P_r和P_θg可以很好地对齐。DG在这种平衡下还没有被很好地理解，这限制了其监测GAN训练的实用性。
利用近端算子，将对偶性差距的概念推广到一般无法实现纳什均衡的GANs训练背景下。我们将近端对偶性间隙(DGλ)的定义如下。
这句话直接遵循了近端平衡点的定义。（eq 10).因此，DG^λ趋于零意味着GAN博弈已经收敛到一个近端平衡。然而，由于GAN被用于学习数据分布，量化GAN收敛的度量也应该提供洞察学习数据分布的本质是很重要的。因此，为了建立DG^λ的适用性，我们研究了它如何与各种GAN公式的真实分布和生成的数据分布之间的差异有关。

4.1. Theoretical Analysis

DG^λ的定义有两个术语–V_Dw和V^G_λw。我们首先建立V_Dw与各种GAN公式中使用的散度(DIV)之间的关系——经典GAN目标V_c的JS散度(JSD(P_θg||P_r))，WGAN目标V_w的 Wasserstein 距离(W_c(P_θg||P_r))，以及F-GAN目标V_f的f−散度(D_f(P_θg||P_r))。在我们的分析中，我们假设对于固定生成器，存在一个使V最大的最优鉴别器(D_w)。
因此，V_Dw(θg)测量生成器G_θg的质量。如果θg是最优的，P_θg覆盖真实分布P_r，那么V_Dw(θg)达到最小值。在P_θg和P_r之间的不匹配情况下，无论是由于支持不足还是样本质量差，V_Dw(θg)将增加，因此使其本身成为监测GAN训练的一个潜在有用度量。然而，V_Dw并没有考虑到鉴别器偏离当前游戏配置的能力。因此，它不能确定游戏是否已经收敛到一个平衡状态。此外，由于V_Dw的最小值将根据GAN的公式而变化，因此它不能作为监测GAN训练的领域不可知度量。另一方面，无论GAN公式如何，DG^λ在接近近端平衡时总是趋向于零。因此，在接下来的结果中，我们分析了DG^λ对三种GAN公式的行为。具体地说，我们证明了在可实现的设置(G是无界容量的；∃θg使P_θg=P_r)和更实际的不可实现的设置(其中G是有界容量)，近端对偶间隙是正的，受P_θg和P_r之间的散度的下限。

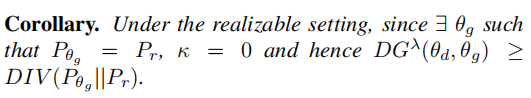
该定理,在可实现的设置下,非平凡地扩展了仅针对经典GAN的DG界的先验结果.

4.2.含义

由于DG^λ是真实数据分布和生成数据分布之间差异的下限，DG^λ→0不仅意味着GAN已经达到平衡，而且生成的分布接近真实数据分布.
这进一步提高了近端平衡的熟练性（adeptness），可以作为gan的一般最优性概念。由于近端均衡不一定是Nash均衡，它也有利于以下有趣的观察：
因此，经验观察认为，尽管收敛到梯度动力学的非纳什吸引子，但它可以生成具有高保真度的真实数据样本，这在理论上是合理的。
在类似的情况上，关于DG^λ行为的一个自然问题是，近端平衡是否构成了一个详尽的平衡概念，其中GANs可以捕获真实的数据分布。确切地说，我们问一个问题：GAN是否收敛到一个解决方案 s.t. P_θg→P_r⇒DG^λ→0？我们的答案从以下关于DG^λ作为λ→0的极端情况的命题开始。

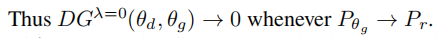
λ的值限制了近端目标(V^λ)中的鉴别器在一个邻域内是最优的。当λ→0，V^λ考虑了整个参数空间(ΘD)上的最优鉴别器。因此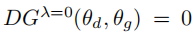
意味着(θd，θg)是一个 Stackelberg平衡。由于所有的近端平衡都是Stackelberg平衡的一个子集，因此 DG^λ=0 将是监测GAN收敛性的理想选择。然而，随着λ的降低，计算V^λ的复杂性迅速增加，并像λ→0一样变得不可行。因此，只有检查GAN构型是否为λ（>0）−近端平衡（λ(> 0)−proximal equilibrium.）才实用。但是，对于一个固定值的λ（>0），DG^λ能监测GANs对所有λ’−近端平衡(λ’−proximal equilibria)的收敛性吗？为了解决这个问题，让我们分别研究这两种情况——(i) λ’≥λ 和(ii) λ’<λ 。以下定理利用近端平衡点解决了(i)的层次性质的情况。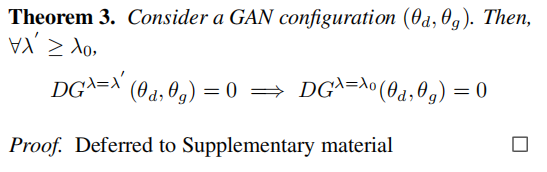
DG^λ’(θd，θg)=0是(θd，θg)是λ’−近端平衡的充分条件。因此，从定理3可以看出，DG^λ能够监测GANs到所有λ’（≥λ）−近端平衡的收敛性。然而，当一个GAN收敛到一个λ’（<λ）−的近端平衡时，DG^λ可能容易出错。下面的定理通过上限限定DG^λ之间的差异和真实数据分布和生成数据分布之间的差异来解决这个问题。
因此，即使GAN收敛到一个λ’（<λ）−的近端平衡，DG^λ可能会产生的误差也是有界的。以前，没有DG定理4所隐含的上界意味着当Pθg接近Pr时，DG不一定需要接近于零。然而，DG^λ排除了这种可能性，因此是一个理论上有基础和稳健的度量，可以作为监测GAN收敛的工具。

4.3. Estimating Proximal Duality Gap

计算GAN配置的真实DG^λ是一项艰巨的任务，因为它涉及到找到非凸函数的最优值。我们通过使用梯度下降来估计V_Dw和V_Gw^λ来近似DG^λ。我们在近端目标V^λ中使用索波列夫范数( Sobolev norm)，

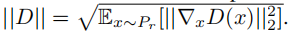
对于由V控制的GAN博弈，估计V_Dw涉及到使用梯度下降优化V(θd，θg) w.r.t θd 。然而，估计V_Gw^λ需要对近端算子进行梯度计算。如(Farnia&Ozdaglar，2020)所示，对于一个GAN objective function V that is smooth w.r.t θd。近端目标(V^λ) w.r.t θg 的梯度 可以用V来得到：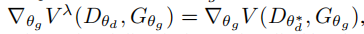
，其中θ_d^*代表近端目标所隐含的最优鉴别器。因此，为了估计V_Gw^λ，我们在每次迭代中都使用梯度下降来获得相应θg的θ_d^∗，并更新θg来最小化V(θ_d^*，θg)。在补充材料中讨论了总体估计过程的算法和相关的计算复杂度。为了确保我们获得对DG^λ的无偏估计，接下来(Grnarova等人，2019)，我们将数据集分成3个不相交的集-S_A、S_B和S_C。我们使用S_A训练GAN，我们使用S_B通过梯度下降找到最坏情况的计数器部分Dw和Gw，S_C评估在获得的最坏情况构型下的目标函数。

5. Experimentation

略。。。
代码

Monitoring GAN training using DGλ

Visualizing the effect of λ

Influencing GAN training using DGλ

。。。

6. Summary and Future Work

GANs突破了学习复杂数据分布的边界。然而，GAN损失曲线的非直观性质使得训练成为一项具有挑战性的任务。我们提出了近端对偶性间隙(DG^λ）作为一种通用的定量工具来监测GAN的训练和理解GAN的收敛性。DG^λ将GAN收敛描述为获得λ−近端平衡的博弈。它还有助于深入了解GAN收敛的本质——当且仅当GAN达到Stackelberg平衡时才会学习真实的数据分布。DG^λ客观量化GAN收敛的能力使其成为调整GAN超参数的有用度量。有几个有待解决的问题可以提高DG^λ的效用，包括确定最优λ，并使DG^λ在GAN公式中的值范围不变。通过近端对偶间隙对GAN收敛的表征为轻松的GAN训练开辟了新的途径。