- 1[IIS] SSL证书安装简明教程_iis express development certificate 如何生成
- 2大数据平台架构技术选型与场景运用_大数据业务场景 技术选型 一般流程
- 3MySQL索引类型简介_mysql四种索引类型
- 4麒麟V10离线rpm安装nginx+php+mariadb环境_银河麒麟v10 rpm包
- 5TableAgent 数据分析智能体简介及应用实战
- 6详解协方差矩阵,相关矩阵,互协方差矩阵(附完整例题分析)【1】_信道相关矩阵
- 7使用VM虚拟机安装centos7.5并安装宝塔面板实现本地搭建测试网站_在一台centos虚拟机上怎么同时安装禅道和宝塔
- 8Codeforces 703D (区间内出现偶数次的数的异或和)_区间内出现偶数次的数异或和
- 9OpenCV(10): 轮廓近似—多边形拟合,边界矩形与边界圆形_opencv 多边形拟合
- 10Bluetooth技术学习笔记 ——ACL连接建立_ble建立acl连接
【C++ OpenCV】图像变换:连接、尺寸、翻转、旋转、仿射变换_c++opencv实现图像连接
赞
踩
目录
图像缩放变换
源码
- void cv::resize(Inputarry src,
- Outputarry dst,
- Size dsize,
- double fx=0,
- double fy=0,
- int interpolation = INTER_LINEAR
- )
-
src - 输入图像。
-
dst - 输出图像;它的大小为 dsize(当它非零时)或从 src.size()、fx 和 fy 计算的大小;dst 的类型与 src 的类型相同。
-
dsize - 输出图像大小;如果它等于零,则计算为:dsize = Size(round(fxsrc.cols), round(fysrc.rows))。dsize 或 fx 和 fy 必须为非零。
-
fx - 沿水平轴的比例因子;当它等于 0 时,它被计算为(double)dsize.width/src.cols
-
fy - 沿垂直轴的比例因子;当它等于 0 时,它被计算为(double)dsize.height/src.rows
-
插值 - 插值方法,在选择插值方法时,需要根据具体的需求和应用场景进行权衡。例如:
-
如果只是简单的缩小图像或者调整图像大小至相对较小的尺寸,最近邻插值 (
cv2.INTER_NEAREST) 可能是一个不错的选择,因为它计算速度快,效果还可以接受。 -
如果需要在图像的放大或缩小过程中保持较好的平滑性,双线性插值 (
cv2.INTER_LINEAR) 是一个常用的选项。 -
如果对图像的质量有更高的要求,并且可以承受更长的计算时间,双三次插值 (
cv2.INTER_CUBIC) 或 Lanczos 插值 (cv2.INTER_LANCZOS4) 可能是更好的选择。
-
-
interpolation algorithm
Enumerator INTER_NEAREST 最近邻插值,该方法选择最接近目标像素的原始像素值作为调整后像素的值。这种插值方法计算速度快,但可能会引入锯齿状边缘和失真。在像素级别的简单放大或缩小时使用。 INTER_LINEAR 双线性插值,该方法使用相邻四个原始像素的加权平均值来计算调整后像素的值。它比最近邻插值提供了更平滑的结果,但可能会导致某些细节的模糊。在图像的放大或缩小过程中使用较多。 INTER_CUBIC 双三次插值,该方法在双线性插值的基础上进一步考虑了相邻像素的颜色变化趋势,以产生更平滑的结果。它比双线性插值计算更复杂,但在放大图像时通常能提供更好的效果。 INTER_AREA resampling using pixel area relation. It may be a preferred method for image decimation, as it gives moire'-free results. But when the image is zoomed, it is similar to the INTER_NEAREST method. 利用像素面积关系进行重采样。这可能是图像抽取的优选方法,因为它给出了无波纹的结果。但是当图像被缩放时,它类似于INTER_NEAREST方法。 INTER_LANCZOS4 8×8邻域上的Lanczos插值,该方法使用Lanczos滤波器进行插值,可以获得更锐利的结果,但计算开销较大。适用于对图像进行较大比例的放大操作。 INTER_LINEAR_EXACT Bit exact bilinear interpolation 比特精确双线性插值 INTER_NEAREST_EXACT Bit exact nearest neighbor interpolation. This will produce same results as the nearest neighbor method in PIL, scikit-image or Matlab. 位精确最近邻插值。这将产生与PIL最近邻法、scikit-image或Matlab相同的结果。 INTER_MAX mask for interpolation codes 插值代码的掩码 WARP_FILL_OUTLIERS flag, fills all of the destination image pixels. If some of them correspond to outliers in the source image, they are set to zero 标志,填充目标图像的所有像素。如果它们中的一些对应于源图像中的异常值,则它们被设置为零 WARP_INVERSE_MAP flag, inverse transformation ,逆变换 For example, linearPolar or logPolar transforms: flag is not set: dst(ρ,ϕ)=src(x,y) flag is set: dst(x,y)=src(ρ,ϕ)
值得注意的是:size和两个double的作用是相同的,fx和fy是指将图像坐标轴进行比例缩放(fx=2就是x轴放大两倍),所以函数使用时只要使用一类即可,两者冲突以dsize为准
dsize =Size( round(fx *src.cols),round(fy *src.rows) )
图像翻转
- void cv::flip(InputArray src,
- OutputArray dst,
- int flipCode);
参数 src 输入矩阵.
参数 dst 输出矩阵,和输入矩阵一样大小。
参数 flipCode 一个标志,决定怎么翻转矩阵; = 0 是围绕着x轴翻转,正值是围绕着y轴翻转,负值是围绕着两个轴一起翻转。
参考 transpose , repeat , completeSymm
图像拼接
纵向拼接
- void cv::vconcat ( const Mat * src,
- size_t nsrc,
- OutputArray dst
- )
- void cv::vconcat ( InputArray src1,
- InputArray src2,
- OutputArray dst
- )
横向拼接
- void cv::hconcat ( const Mat * src,
- size_t nsrc,
- OutputArray dst
- )
- void cv::hconcat ( InputArray src1,
- InputArray src2,
- OutputArray dst
- )
-
值得注意的是:横向拼接,那么两个图像的高度应该相同,纵向拼接两个图像的宽度应该相同
图像插值原理
图像经过一系列处理,其像素矩阵的尺寸、大小发生改变,那么我对应的其中的每个像素的像素值如何变化?如果变换后的像素矩阵比原矩阵行和列都大,或者都小,那么变换后的像素矩阵可能就多出来一些像素或者被压缩,这些像素位置的值怎么确定?
情况1:两个像素经过变换后对应同一个位置

情况2:两个相邻像素经过变换后变得不再相邻,中间的位置像素如何确定
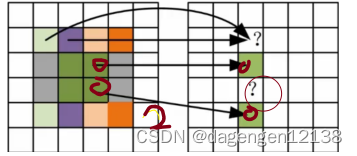
插值简单来说就是用已知的像素值去推测未知的像素值,常见的插值方法有:最邻近法、线性插值法、双线性插值法。本文重点介绍双线性插值法,来源于博文
在两个方向分别进行一次线性插值(首先在一个方向上使用线性插值,然后再在另一个方向上使用线性插值执行双线性插值。尽管每个步骤在采样值和位置上都是线性的,但是插值总体上不是线性的,而是在采样位置上是二次的。)
作用
一般用于重新采样图像和纹理。 计算四个周围纹理像素的属性(颜色,透明度等)的加权平均值,并将其应用于屏幕像素。 (简单来说,我要求一个已知坐标的像素值,先去找他四个周围已知像素的坐标通常是最邻近的四个像素值,通过两次单线性插值,找到他的像素值是多少)
单线性插值
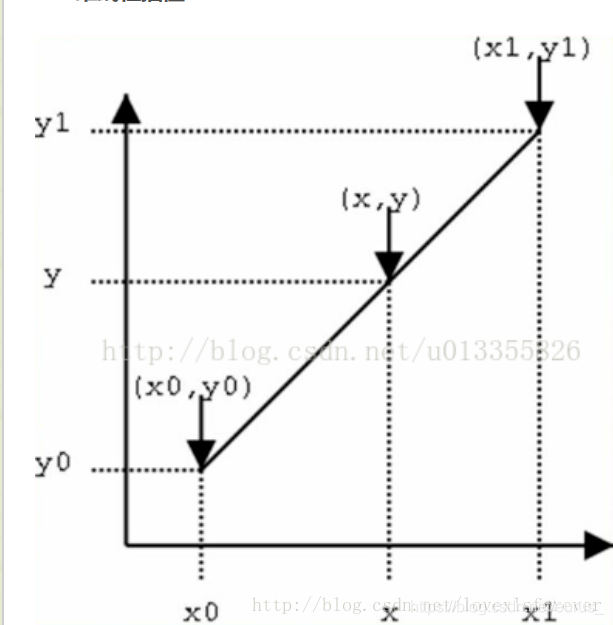
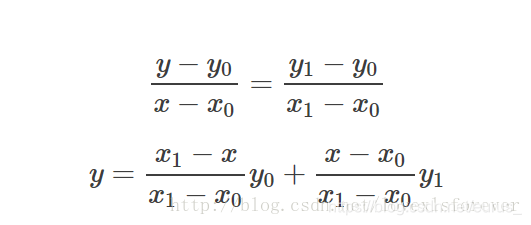
仔细看就是用x和x0,x1的距离作为一个权重,用于y0和y1的加权。双线性插值本质上就是在两个方向上做线性插值。
双线性插值的公式
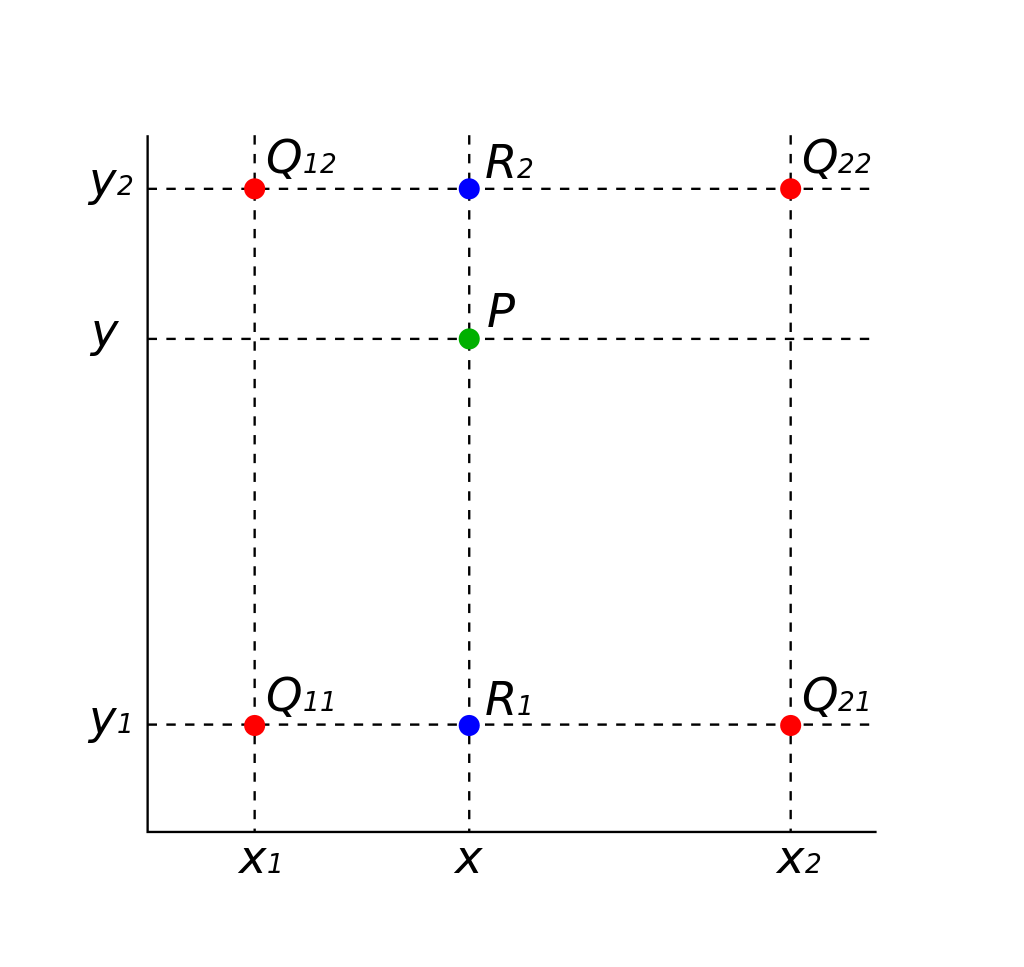
如图所示,我们需要求P点的像素值。我们已知了Q11、Q21、Q12、Q22、P的坐标。也知道Q11、Q21、Q12、Q22的像素值。所以先用关于X的单线性插值去分别计算R1、R2的像素值:
在等式中的字母f(Q11)、f(Q12)、f(Q21)、f(Q22)、x1、x2、x都是已知的,求出的f(x,y1)与f(x,y2)即为R1、R2的像素值。 再使用关于y方向的单线性插值计算P点的像素值 得出:
在右边的等式中的字母y1、y2、y都是已知的,f(x,y1)与f(x,y2)即为上一个式子中求出的R1、R2像素值。
双线性插值的例子
举个栗子:
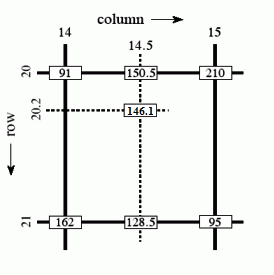
如右侧示例所示,可以通过在第20行和第21行的第14列和第15列的值之间进行线性内插,来计算计算为在第20.2行第14.5列处的像素处的强度值.(这里也正好说明了一般使用最相邻的像素点)
双线性插值的直观展示
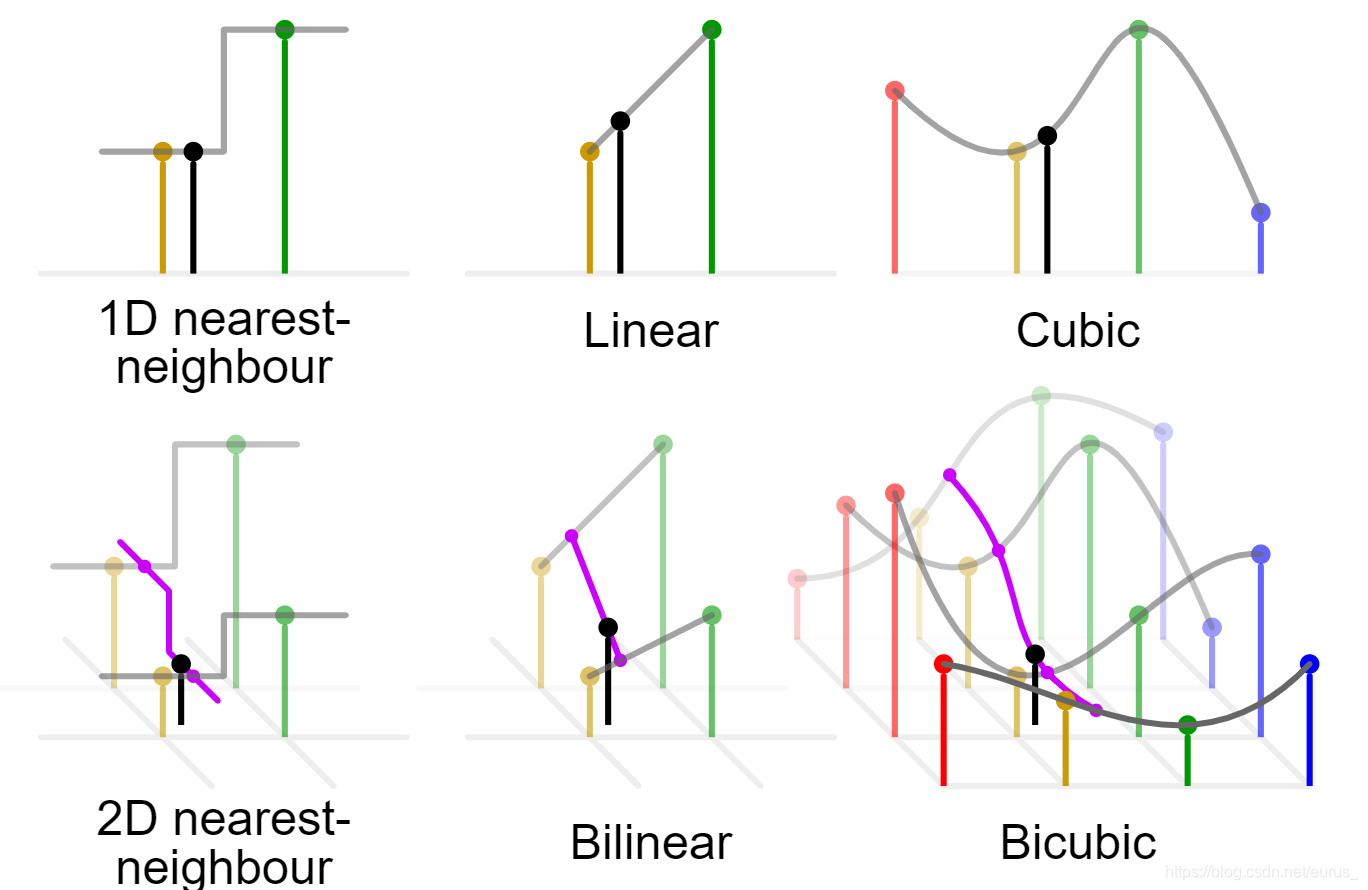
意义
此算法减少了由于将图像调整大小为非整数缩放因子而导致的某些视觉失真
仿射变换
仿射变换是一种二维空间中的几何变换,仿射变换常用于对图像进行平移、旋转、缩放、错切等线性变换操作,也称三点变换。该变换能够保持图像的平直性和平行性。平直性是指图像经过仿射变换后,直线仍然是直线;平行性是指图像在完成仿射变换后,平行线仍然是平行线。
使用时机:
仿射变换在图像处理和计算机视觉领域中具有广泛的应用,常用于以下情况和目的:
-
平移和旋转校正:当图像需要进行平移或旋转校正时,可以使用仿射变换。例如,在图像拍摄过程中,可能由于相机姿态或运动造成图像倾斜或旋转,通过仿射变换可以将图像校正为水平或垂直方向。
-
图像缩放和裁剪:通过调整仿射变换矩阵中的缩放参数,可以实现图像的缩放和裁剪操作。缩放可用于调整图像的大小,而裁剪可用于提取感兴趣区域或改变图像的长宽比。
-
图像变形和纠正:仿射变换可用于对图像进行形状变换,例如错切变换。这在一些特殊应用中很有用,比如文档扫描中的透视校正,可以将扭曲的文档图像转换为矩形形状。
-
特征对齐和匹配:在计算机视觉中,对于特征点的定位和匹配,可以使用仿射变换将一组特征点对齐到另一组特征点,以实现图像配准、目标跟踪等任务。
-
图像合成和重构:通过应用仿射变换,可以将不同尺度、方向或形状的图像进行合成或重构。例如,在图像拼接中,可以使用仿射变换将多个图像进行对齐,以创建全景图像。
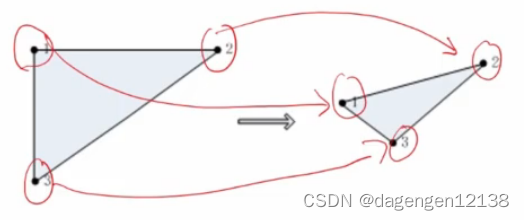
当变换前和变换后的三点坐标确定,则我的仿射变换矩阵M是唯一存在的。
仿射变换矩阵

矩阵A负责将像素点进行旋转,矩阵B负责平移
仿射变换原理
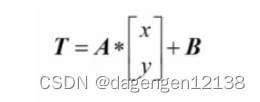
程序源码:
- void::warpAffine( INputarry src,
- Outputarry dst,
- InputArry M,
- size dsize,
- int flags= INTER_LINEAR,
- int borderMode = BOARDER_CONSTANT,
- CONST Scalar& borderValue = Scalar
- )
| Enumerator | ||
|---|---|---|
| BORDER_CONSTANT | iiiiii|abcdefgh|iiiiiii with some specified i | 特定值(用的多) |
| BORDER_REPLICATE | aaaaaa|abcdefgh|hhhhhhh | 两端复制 |
| BORDER_REFLECT | fedcba|abcdefgh|hgfedcb | 倒叙填充 |
| BORDER_WRAP | cdefgh|abcdefgh|abcdefg | 正序填充 |
| BORDER_REFLECT_101 | gfedcb|abcdefgh|gfedcba | |
| BORDER_TRANSPARENT | uvwxyz|abcdefgh|ijklmno | |
| BORDER_REFLECT101 | same as BORDER_REFLECT_101 | |
| BORDER_DEFAULT | same as BORDER_REFLECT_101 | |
| BORDER_ISOLATED | do not look outside of ROI |
BORDER_CONSTANT使用的最多,因为设置特定值为0,填充区域为黑色,而我们通常不需要获取填充区域的图片信息,所以研究填充区的像素矩阵是没有什么意义的。
图像旋转
在opencv中并没有直接实现啊图像旋转的函数,而是通过getRotationMatriix2D()得到旋转矩阵后再调用仿射变换函数来实现图像旋转。
源码
- Mat cv::getRotationMatrix2D(Point2f center,
- double angle,
- double scale
- )
-
center 图像旋转中心位置,输入值,通常定义Point2f center1(img.rows/2.0 , img.cols/2.0)
-
angle 旋转角度
-
scale 两个轴的比例因子,可以实现旋转过程中的图像缩放

其中:
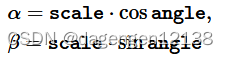
注意:该函数是有返回值的为Mat类型
定义一个Mat类型矩阵接受返回值后,将其作为仿射函数的M参数,便可以实现图像旋转。
获取仿射矩阵
Mat cv::getAffineTransform(const Point2f src[],
const Point2f dst[]
)
-
src[] :原图像中的3个像素坐标,是一个数组,其内的数据类型是Point2f
-
dst[]:目标图像中的三个像素坐标,是一个数组,其内的数据类型是Point2f
实操
一、实现图像旋转
- #include<opencv2/opencv.hpp>
- #include<iostream>
- #include<vector>
-
- using namespace std;
- using namespace cv;
-
-
- int main()
- {
- Mat img = imread("E://学习//OPEN-CV学习//lena.png");
- if (img.empty())
- {
- cout << "读取失败!" << endl;
- return -1;
- }
-
- //实现旋转操作
- Point2f center (img.rows / 2.0, img.cols / 2.0);
- double angle = 30;
- double scale = 0.5;
- Size dsize(img.rows, img.cols);
- Mat rotation,dst;
- rotation = getRotationMatrix2D(center, angle, scale);
-
- warpAffine(img, dst, rotation, dsize);
- imshow("dst", dst);
-
- waitKey(1);
- return 0;
- }

得到旋转矩阵结果和旋转后的结果图

二、根据定义的三个点实现仿射变换,并且求取仿射变换矩阵
- #include<opencv2/opencv.hpp>
- #include<iostream>
- #include<vector>
-
- using namespace std;
- using namespace cv;
-
-
- int main()
- {
- Mat img = imread("E://学习//OPEN-CV学习//lena.png");
- if (img.empty())
- {
- cout << "读取失败!" << endl;
- return -1;
- }
-
- //实现旋转操作
- Point2f center (img.rows / 2.0, img.cols / 2.0);
- double angle = 30;
- double scale = 0.5;
- Size dsize(img.rows, img.cols);
- Mat rotation,dst;
- rotation = getRotationMatrix2D(center, angle, scale);
-
- warpAffine(img, dst, rotation, dsize);
- imshow("dst", dst);
-
- Point2f ori[3];
- Point2f res[3];
- //原图像的三个边角点
- ori[0] = Point2f (0, 0);
- ori[1] = Point2f (0, (float)(img.cols-1));
- ori[2] = Point2f ((float)(img.rows-1), (float)(img.cols - 1));
- //想仿射变换的三个点
- res[0] = Point2f((float)(img.rows*0.10), (float)(img.cols*0.20));
- res[1] = Point2f((float)(img.rows * 0.15), (float)(img.cols * 0.70));
- res[2] = Point2f((float)(img.rows * 0.65), (float)(img.cols * 0.90));
- //获取仿射变换矩阵
- Mat rotation1, dst1;
- rotation1 = getAffineTransform(ori, res);
- warpAffine(img, dst1, rotation1, dsize);
- imshow("dst1", dst1);
-
-
- waitKey(1);
- return 0;
- }


得到仿射矩阵和仿射变换后的结果图。