- 1轻松项目管理01-认知项目管理_传统项目管理阶段的标志性事件有哪些?
- 2数字反转(升级版) 洛谷P1553_p1553数字反转(升级版)
- 3Jmeter中Content-Type设置(记一次排错)_jmeter信息头管理器content-type
- 4Python将时间戳转换为实际时间的方法_python时间戳转换成时间
- 50001.关于django中的Mixin以及原理解析_loginrequiredmixin
- 6《动手学深度学习(PyTorch版)》笔记7.1
- 7Python_微博热搜&保存数据库_微博热搜数据库
- 8曲线生成 | 图解贝塞尔曲线生成原理(附ROS C++/Python/Matlab仿真)_贝塞尔曲线模拟
- 9产品经理面经|当面试官问你还有什么问题?
- 10linux top命令详解_top linux
随机森林回归matlab代码_集成算法 随机森林回归模型
赞
踩
所有的参数,属性与接口,全部和随机森林分类器一致。仅有的不同就是回归树与分类树的不同,不纯度的指标, 参数Criterion不一致。
RandomForestRegressor(n_estimators='warn', criterion='mse', max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features='auto', max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None, bootstrap=True, oob_score=False, n_jobs=None, random_state=None, verbose=0, warm_start=False)重要参数,属性与接口
criterion
回归树衡量分枝质量的指标,支持的标准有三种
- 输入
"mse"使用均方误差mean squared error(MSE),父节点和叶子节点之间的均方误差的差额将被用来作为特征选择的标准,这种方法通过使用叶子节点的均值来最小化L2损失。 - 输入
"friedman_mse"使用费尔德曼均方误差,这种指标使用弗里德曼针对潜在分枝中的问题改进后的均方误差。 - 输入
"mae"使用绝对平均误差MAE(mean absolute error),这种指标使用叶节点的中值来最小化L1损失。
其中是样本数量,i是每一个数据样本,是模型回归出的数值,是样本点i实际的数值标签。所以MSE的本质是样本真实数据与回归结果的差异。在回归树中,MSE不只是我们的分枝质量衡量指标,也是我们最常用的衡量回归树回归质量的指标,当我们在使用交叉验证,或者其他方式获取回归树的结果时,我们往往选择均方误差作为我们的评估(在分类树中这个指标是score代表的预测准确率)。在回归中,我们追求的是,MSE越小越好。
然而,回归树的接口score返回的是R平方,并不是MSE。此处可参考线性回归中模型评估指标。
最重要的属性和接口,都与随机森林的分类器相一致,还是apply, fit, predict和score最为核心。值得一提的是,随机森林回归并没有predict_proba这个接口,因为对于回归来说,并不存在一个样本要被分到某个类别的概率问题,因此没有predict_proba这个接口。
例子
from sklearn.datasets import load_bostonfrom sklearn.model_selection import cross_val_scorefrom sklearn.ensemble import RandomForestRegressorboston = load_boston()regressor = RandomForestRegressor(n_estimators=100,random_state=0)cross_val_score(regressor, boston.data, boston.target, cv=10 ,scoring = "neg_mean_squared_error")sorted(sklearn.metrics.SCORERS.keys())返回十次交叉验证的结果,注意在这里,如果不填写scoring = "neg_mean_squared_error",交叉验证默认的模型衡量指标是R平方,因此交叉验证的结果可能有正也可能有负。而如果写上scoring,则衡量标准是负MSE,交叉验证的结果只可能为负。
实例:⽤随机森林回归填补缺失值
在之前缺失值处理文章中提到运用随机森林回归填补缺失值,我们来看看具体如何操作。
导包
import numpy as npimport pandas as pdimport matplotlib.pyplot as pltfrom sklearn.datasets import load_bostonfrom sklearn.impute import SimpleImputerfrom sklearn.ensemble import RandomForestRegressorfrom sklearn.model_selection import cross_val_score数据准备
以波⼠顿数据集为例,导⼊完整的数据集并探索
dataset = load_boston()dataset.data.shape#总共506*13=6578个数据X, y = dataset.data, dataset.targetn_samples = X.shape[0]n_features = X.shape[1]生产缺失值
rng = np.random.RandomState(0)missing_rate = 0.5n_missing_samples = int(np.floor(n_samples * n_features * missing_rate))#np.floor向下取整,返回.0格式的浮点数所有数据要随机遍布在数据集的各⾏各列当中,⽽⼀个缺失的数据会需要⼀个⾏索引和⼀个列索引如果能够创造⼀个数组,包含3289个分布在0~506中间的⾏索引,和3289个分布在0~13之间的列索引,那我们就可以利⽤索引来为数据中的任意3289个位置赋空值。
我们现在采样3289个数据,远远超过样本量506,所以使⽤随机抽取的函数randint。但如果需要的数据量⼩于我们的样本量506,那我们可以采⽤np.random.choice来抽样,choice会随机抽取不重复的随机数,因此可以帮助我们让数据更加分散,确保数据不会集中在⼀些⾏中。
missing_features_index = rng.randint(0,n_features,n_missing_samples)missing_samples_index = rng.randint(0,n_samples,n_missing_samples)# missing_samples=rng.choice(dataset.data.shape[0],n_missing_samples,replace=False)X_missing = X.copy()y_missing = y.copy()X_missing[missing_samples, missing_features] = np.nanX_missing = pd.DataFrame(X_missing)# 转换成DataFrame是为了后续⽅便各种操作,# numpy对矩阵的运算速度快,但是在索引等功能上却不如pandas来得好⽤然后我们⽤0,均值和随机森林来填写这些缺失值,然后查看回归的结果如何
#使⽤均值进⾏填补from sklearn.impute import SimpleImputerimp_mean = SimpleImputer(missing_values=np.nan, strategy='mean')X_missing_mean = imp_mean.fit_transform(X_missing)#使⽤0进⾏填补imp_0 = SimpleImputer(missing_values=np.nan, strategy="constant",fill_value=0)X_missing_0 = imp_0.fit_transform(X_missing)随机森林填补
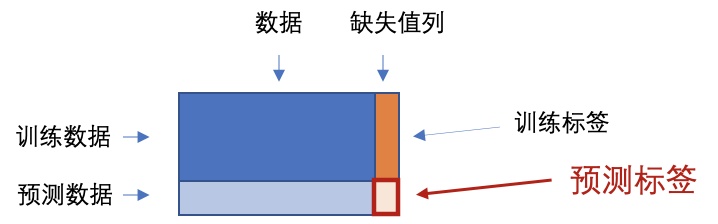
使⽤随机森林回归填补缺失值任何回归都是从特征矩阵中学习,然后求解连续型标签y的过程,之所以能够实现这个过程,是因为回归算法认为,特征矩阵和标签之前存在着某种联系。实际上,标签和特征是可以相互转换的,⽐如说,在⼀个"⽤地区,环境,附近学校数量"预测"房价"的问题中,我们既可以⽤"地区","环境","附近学校数量"的数据来预测"房价",也可以反过来,⽤"环境","附近学校数量"和"房价"来预测"地区"。⽽回归填补缺失值,正是利⽤了这种思想。
对于⼀个有n个特征的数据来说,其中特征T有缺失值,我们就把特征T当作标签,其他的n-1个特征和原本的标签组成新的特征矩阵。那对于T来说,它没有缺失的部分,就是我们的Y_test,这部分数据既有标签也有特征,⽽它缺失的部分,只有特征没有标签,就是我们需要预测的部分。
特征T不缺失的值对应的其他n-1个特征 + 本来的标签:X_train
特征T不缺失的值:Y_train
特征T缺失的值对应的其他n-1个特征 + 本来的标签:X_test
特征T缺失的值:未知,我们需要预测的Y_test
这种做法,对于某⼀个特征⼤量缺失,其他特征却很完整的情况,⾮常适⽤。
那如果数据中除了特征T之外,其他特征也有缺失值怎么办?答案是遍历所有的特征,从缺失最少的开始进⾏填补(因为填补缺失最少的特征所需要的准确信息最少)。填补⼀个特征时,先将其他特征的缺失值⽤0代替,每完成⼀次回归预测,就将预测值放到原本的特征矩阵中,再继续填补下⼀个特征。每⼀次填补完毕,有缺失值的特征会减少⼀个,所以每次循环后,需要⽤0来填补的特征就越来越少。当进⾏到最后⼀个特征时(这个特征应该是所有特征中缺失值最多的),已经没有任何的其他特征需要⽤0来进⾏填补了,⽽我们已经使⽤回归为其他特征填补了⼤量有效信息,可以⽤来填补缺失最多的特征。遍历所有的特征后,数据就完整,不再有缺失值了。
X_missing_reg = X_missing.copy()sortindex = np.argsort(X_missing_reg.isnull().sum(axis=0)).valuesfor i in sortindex: #构建我们的新特征矩阵和新标签 df = X_missing_reg fillc = df.iloc[:,i] df = pd.concat([df.iloc[:,df.columns != i],pd.DataFrame(y_full)],axis=1) #在新特征矩阵中,对含有缺失值的列,进⾏0的填补 df_0 =SimpleImputer(missing_values=np.nan, strategy='constant',fill_value=0).fit_transform(df) #找出我们的训练集和测试集 Ytrain = fillc[fillc.notnull()] Ytest = fillc[fillc.isnull()] Xtrain = df_0[Ytrain.index,:] Xtest = df_0[Ytest.index,:] #⽤随机森林回归来填补缺失值 rfc = RandomForestRegressor(n_estimators=100) rfc = rfc.fit(Xtrain, Ytrain) Ypredict = rfc.predict(Xtest) #将填补好的特征返回到我们的原始的特征矩阵中 X_missing_reg.loc[X_missing_reg.iloc[:,i].isnull(),i] = Ypredict建模
#对所有数据进⾏建模,取得MSE结果X = [X_full,X_missing_mean,X_missing_0,X_missing_reg]mse = []std = []for x in X: estimator = RandomForestRegressor(random_state=0, n_estimators=100) scores = cross_val_score(estimator,x,y_full,scoring='neg_mean_squared_error', cv=5).mean() mse.append(scores * -1)可视化
x_labels = ['Full data', 'Zero Imputation', 'Mean Imputation', 'Regressor Imputation']colors = ['r', 'g', 'b', 'orange']plt.figure(figsize=(12, 6))ax = plt.subplot(111)for i in np.arange(len(mse)): ax.barh(i, mse[i],color=colors[i], alpha=0.6, align='center') ax.set_title('Imputation Techniques with Boston Data')ax.set_xlim(left=np.min(mse) * 0.9,right=np.max(mse) * 1.1)ax.set_yticks(np.arange(len(mse)))ax.set_xlabel('MSE')ax.set_yticklabels(x_labels)plt.show()随机森林调参
| 参数 | 对模型在未知数据上的评估性能的影响 | 影响程度 |
|---|---|---|
| n_estimators | 提升⾄平稳,n_estimators↑,不影响单个模型的复杂度 | ???? |
| max_depth | 有增有减,默认最⼤深度,即最⾼复杂度,向复杂度降低的⽅向调参max_depth↓,模型更简单,且向图像的左边移动 | ??? |
| min_samples _leaf | 有增有减,默认最⼩限制1,即最⾼复杂度,向复杂度降低的⽅向调参min_samples_leaf↑,模型更简单,且向图像的左边移动 | ?? |
| min_samples_split | 有增有减,默认最⼩限制2,即最⾼复杂度,向复杂度降低的⽅向调参min_samples_split↑,模型更简单,且向图像的左边移动 | ?? |
| max_features | 有增有减,默认auto,是特征总数的开平方,位于中间复杂度,既可以 向复杂度升高的方向,也可以向复杂度降低的方向调参 max_features↓,模型更简单,图像左移 max_features↑,模型更复杂,图像右移 max_features是唯⼀的,既能够让模型更简单,也能够让模型更复杂的参数,所以在调整这个参数的时候,需要考虑我们调参方向 | ? |
| criterion | 有增有减,一般使用gini |
推荐阅读




